| Citation: |
Ahmed AL-Taweel, Saqib Hussain, Xiaoshen Wang. SUPERCLOSENESS ANALYSIS OF STABILIZER FREE WEAK GALERKIN FINITE ELEMENT METHOD FOR CONVECTION-DIFFUSION EQUATIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1963-1981. doi: 10.11948/20200298
|
SUPERCLOSENESS ANALYSIS OF STABILIZER FREE WEAK GALERKIN FINITE ELEMENT METHOD FOR CONVECTION-DIFFUSION EQUATIONS
-
Abstract
Recently, a stabilizer free weak Galerkin (SFWG) method is proposed in [
14 ], which is easier to implement and more efficient. In this paper, we developed an SFWG scheme for solving the general second-order elliptic problem on triangular meshes in 2D. This new SFWG method will dramatically reduce the error between the $ L^{2} $-projection of the exact solution and the numerical solution. -
-
References
[1] A. Al-Taweel and X. Wang, A note on the optimal degree of the weak gradient of the stabilizer free weak Galerkin finite element method, Applied Numerical Mathematics, 2020, 150, 444-451. doi: 10.1016/j.apnum.2019.10.009 [2] A. Al-Taweel and X. Wang, The lowest-order stabilizer free Weak Galerkin Finite Element Methods, Applied Numerical Mathematics, 2020, 157, 434-445. doi: 10.1016/j.apnum.2020.06.012 [3] A. Al-Taweel, S. Hussain and X. Wang, A stabilizer free weak Galerkin finite element method for parabolic equation, Journal of Computational and Applied Mathematics, 2021, 113373. [4] A. Al-Taweel, S. Hussain, R. Lin and P. Zhu, A stabilizer free weak Galerkin finite element method for general second-order elliptic problem, International Journal of Numerical Analysis and Modeling, 2021 (to appear). [5] A. Al-Taweel, X. Wang, X. Ye and S. Zhang, A stabilizer free weak Galerkin element method with supercloseness of order two, arXiv: 2004.11192v1, 2020. [6] M. Cheichan, H. Kashkool and F. Gao, A weak Galerkin finite element method for solving nonlinear convection-diffusion problems in two dimensions, International Journal of Applied and Computational Mathematics, 2019, 5(2), 36. doi: 10.1007/s40819-019-0621-3 [7] M. Cheichan, H. Kashkool and F. Gao, A weak Galerkin finite element method for solving nonlinear convection-diffusion problems in two dimensions, Journal of Mathematics and Computation, 2019, 354, 149-163. doi: 10.1016/j.amc.2019.02.043 [8] B. Deka, P. Roy and N. Kumar, Weak Galerkin finite element method combined with Crank-Nicolson scheme for Parabolic interface problems, Journal of Applied Analysis and Computation, 2020, 10(4), 1433-1442. doi: 10.11948/20190218 [9] F. Gao, S. Zhang and P. Zhu, Modified weak Galerkin method with weakly imposed boundary condition for convection-dominated diffusion equations, Journal of Applied Numerical Mathematics, 2020, 157, 490-504. doi: 10.1016/j.apnum.2020.07.010 [10] R. Lin, X. Ye, S. Zhang and P. Zhu, A Weak Galerkin Finite Element Method for Singularly Perturbed Convection-Diffusion-Reaction Problems, SIAM Journal on Numerical Analysis, 2018, 56(3), 1482-1497. doi: 10.1137/17M1152528 [11] R. Lin, X. Ye, S. Zhang and P. Zhu, Analysis Of A DG Method For Singularly Perturbed Convection- Diffusion Problems, Journal of Applied Analysis and Computation, 2020, 10(3), 830-841. doi: 10.11948/20180164 [12] H. G. Roos, M. Stynes and L. Tobiska, Robust numerical methods for singularly perturbed differential equations, in: Convection–Diffusion–Reaction and Flow Problems, second edition, in: Springer Series in Computational Mathematics, vol. 24, Springer-Verlag, Berlin, 2008. [13] J. Wang and X. Ye, A Weak Galerkin mixed finite element method for second-order elliptic problems, Math. Comp. 2014, 83, 2101-2126. doi: 10.1090/S0025-5718-2014-02852-4 [14] X. Ye and S. Zhang, A stabilizer-free weak Galerkin finite element method on polytopal meshes, Journal of Computational and Applied Mathematics. 2020, 372, 112699. [15] X. Ye and S. Zhang, A stabilizer-free pressure-robust finite element method for the Stokes equations, arXiv: 2006.11853, 2020. [16] P. Zhu and X. Wang, A Least Square Based Weak Galerkin Finite Element Method for Second Order Elliptic Equations in Non-Divergence Form, Acta Mathematica Scientia, 2020, 40, 1553-1562. doi: 10.1007/s10473-020-0521-y -
-
Figures(6) / Tables(7)
Export File
Citation
Ahmed AL-Taweel, Saqib Hussain, Xiaoshen Wang. SUPERCLOSENESS ANALYSIS OF STABILIZER FREE WEAK GALERKIN FINITE ELEMENT METHOD FOR CONVECTION-DIFFUSION EQUATIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1963-1981. doi: 10.11948/20200298
Format
Content
DownLoad:
-
Figure 1. Example 1: Plot of the
$ L^2 $ -error and convergence rate for$ \left( P_{1}(T), P_{2}(e), [P_{2}(T)]^{2}\right) $ and$ h = 1/64 $ : (a) SFWG method (2.5); (b) WG method. -
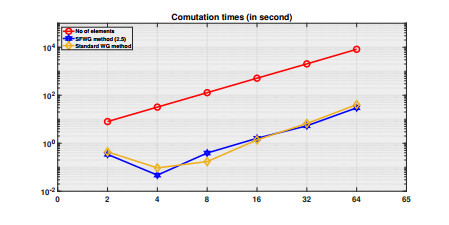
Figure 2. Example 1: Comparison of computation times for the SFWG algorithm 1 and the WG algorithm using
$ \left( P_{1}(T), P_{2}(e), [P_{2}(T)]^{2}\right) $ elements. -
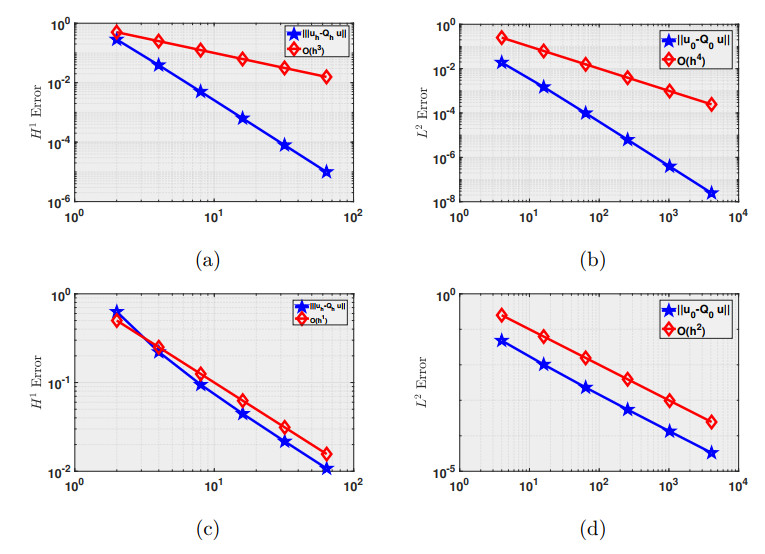
Figure 3. Example 2: Plot of the errors and convergence rate for
$ \left( P_{1}(T), P_{2}(e), [P_{2}(T)]^{2}\right) $ and$ h = 1/64 $ , for errors measured by$ \|Q_{0}u-u\| \;{\rm{ and }}\; bar Q_{h}u-ubar $ : (a), (b) SFWG method (2.5); (c), (d) WG method. -
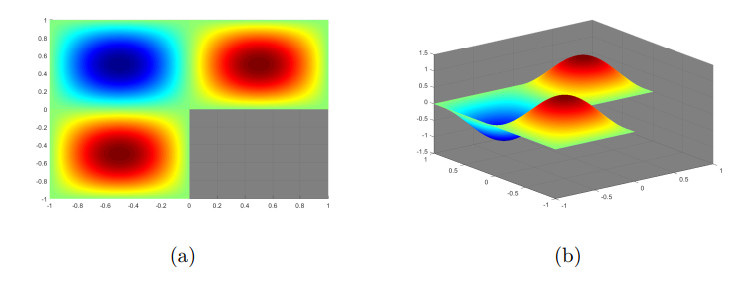
Figure 4. Example 2: Plot of numerical solutions for
$ \left( P_{1}(T), P_{2}(e), [P_{2}(T)]^{2}\right) $ element using SFWG method (2.5)and$ h = 1/64 $ : (a) 2D plot; (b) 3D plot. -
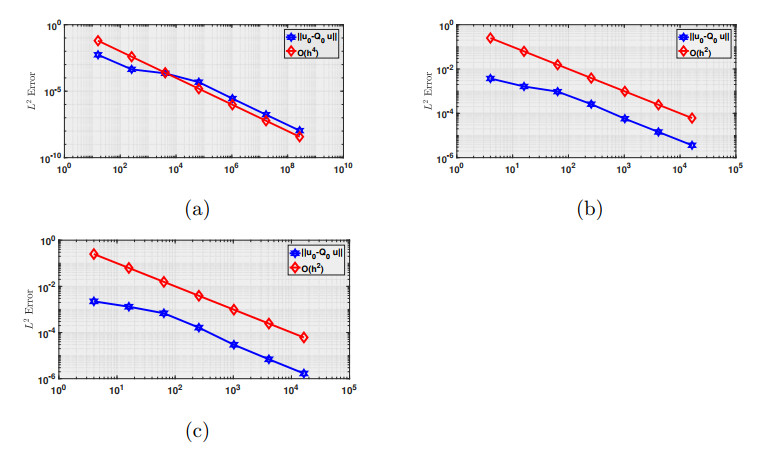
Figure 5. Example 3: Plot of the errors and convergence rate for errors measured by
$ \|Q_{0}u-u\| $ and$ h = 1/128 $ : (a) SFWG method (2.5); (b) old version of SFWG method with$ (P_{1}(T), P_{2}(e), [P_{2}(T)]^{2}) $ elements, (c) WG method. -
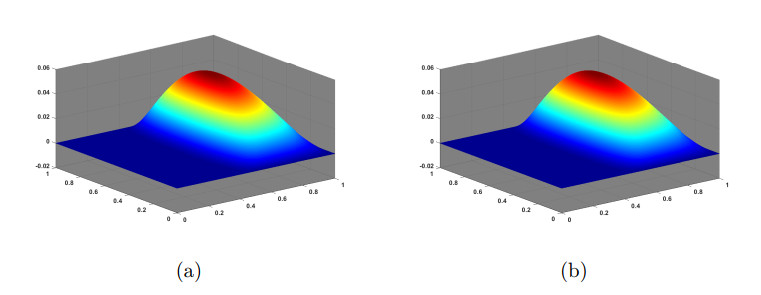
Figure 6. Example 3: Plot of: (a) SFWG solutions (2.5); (b) Exact solution, for
$ \left( P_{1}(T), P_{2}(e), [P_{2}(T)]^{2}\right) $ and$ h = 1/128 $ .