| Citation: | Xiaoming Yang, Guo Lin, Jianing Yang. ASYMPTOTIC SPREADING IN A COMPETITION SYSTEM WITH NONLOCAL DISPERSAL[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1951-1962. doi: 10.11948/20200290 |
ASYMPTOTIC SPREADING IN A COMPETITION SYSTEM WITH NONLOCAL DISPERSAL
-
Abstract
This paper is concerned with the long time behavior of a competition system with nonlocal dispersal. When the initial conditions of both unknown functions satisfy proper decay behavior, we obtain the rough spreading speed of one unknown function and show the upper and lower bounds of spreading speed of another unknown function. Moreover, a numerical example is given to illustrate our analytic results. Our conclusions imply that both the linear part and nonlinear part in reaction terms may affect the spreading speeds. Moreover, in such a competitive system with constant coefficients, we may observe the propagation terraces in some component.
-
Keywords:
- Noncooperative system /
- upper and lower solutions /
- auxiliary system
-

-
References
[1] D. G. Aronson and H. F. Weinberger, Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation, In: Partial Differential Equations and Related Topics, (Edited by J.A. Goldstein), Lecture Notes in Mathematics, Springer, Berlin, 1975,446, 5-49. [2] X. Bao, W. Li and W. Shen, Traveling wave solutions of Lotka-Volterra competition systems with nonlocal dispersal in periodic habitats, J. Differential. Equations., 2016,260(12), 8590-8637. doi: 10.1016/j.jde.2016.02.032 [3] X. Bao, W. Shen and Z. Shen, Spreading speeds and traveling waves for space-time periodic nonlocal dispersal cooperative systems, Commun. Pure Appl. Anal., 2019, 18(1), 361-396. doi: 10.3934/cpaa.2019019 [4] P. W. Bates, On some nonlocal evolution equations arising in materials science, Fields Inst. Commun, AMS, Providence, 2006, 48, 13-52. [5] N. F. Britton, Reaction-diffusion equations and their applications to biology, Academic Press, London, 1986. [6] R. S. Cantrell and C. Cosner, Spatial Ecology via Reaction-Diffusion Equations, John Wiley & Sons, Ltd., Boca, 2003. [7] L. Du, W. Li and S. Wu, Pulsating fronts and front-like entire solutions for a reaction-advection-diffusion competition model in a periodic habitat, J. Differential. Equations., 2019,266(12), 8419-8458. doi: 10.1016/j.jde.2018.12.029 [8] A. Ducrot, T. Giletti and H. Matano, Existence and convergence to a propagating terrace in one-dimensional reaction-diffusion equations, Trans. Amer. Math. Soc., 2014,366(10), 5541-5566. doi: 10.1090/S0002-9947-2014-06105-9 [9] J. Fang and X. Zhao, Traveling waves for monotone semiflows with weak compactness, SIAM J. Math. Anal., 2014, 46(6), 3678-3704. doi: 10.1137/140953939 [10] P. Fife, Some nonclassical trends in parabolic and parabolic-like evolutions, In: Trends in Nonlinear Analysis (Ed. by M. Kirkilionis, S. Kr$\ddot{o}$mker, R. Rannacher, F. Tomi), pp. 153-191, Springer, Berlin, 2003. [11] L. Girardin and K. Y. Lam, Invasion of open space by two competitors: spreading properties of monostable two-species competition-diffusion systems, Proc. Lond. Math. Soc., 2019,119(5), 1279-1335. doi: 10.1112/plms.12270 [12] G. Hetzer, T. Nguyen and W. Shen, Coexistence and extinction in the Lotka-Volterra competition model with nonlocal dispersal, Commun. Pure Appl. Anal., 2013, 11(5), 1699-1722. [13] Y. Jin and X. Zhao, Spatial dynamics of a periodic population model with dispersal, Nonlinearity, 2009, 22(5), 1167-1189. doi: 10.1088/0951-7715/22/5/011 [14] M. A. Lewis, S. V. Petrovskii and J. R. Sergei, The mathematics behind biological invasions, Interdisciplinary Applied Mathematics, 44, Springer, Cham, 2016. [15] W. Li, L. Zhang and G. Zhang, Invasion entire solutions in a competition system with nonlocal dispersal, Discrete Contin. Dyn. Syst., 2015, 35(4), 1531-1560. doi: 10.3934/dcds.2015.35.1531 [16] X. Liang and X. Zhao, Asymptotic speeds of spread and traveling waves for monotone semiflows with applications, Comm. Pure Appl. Math., 2006, 60(1), 1-40. [17] G. Lin and W. Li, Asymptotic spreading of competition diffusion systems: The role of interspecific competitions, Euro. J. Appl. Math., 2012, 23(6), 669-689. doi: 10.1017/S0956792512000198 [18] R. Lui, Biological growth and spread modeled by systems of recursions. I. Mathematical theory, Math. Biosci., 1989, 93(2), 269-295. doi: 10.1016/0025-5564(89)90026-6 [19] J. D. Murray, Mathematical Biology: I. An Introduction, Third edition, Springer-Verlag, New York, 2002. [20] J. D. Murray, Mathematical Biology: â…¡. Spatial Models and Biomedical Applications, Third edition, Springer-Verlag, New York, 2003. [21] S. Pan, Traveling wave solutions in nonlocal dispersal models with nonlocal delays, J. Korean Math. Soc., 2014, 51(4), 703-719. doi: 10.4134/JKMS.2014.51.4.703 [22] N. Shigesada and K. Kawasaki, Biological Invasions: Theory and Practice, Oxford University Press, Oxford, 1997. [23] M. Tang and P. Fife, Propagating fronts for competing species equations with diffusion, Arch. Ration. Mech. Anal., 1980, 73(1), 69-77. doi: 10.1007/BF00283257 [24] H. F. Weinberger, M. A. Lewis and B. Li, Analysis of linear determinacy for spread in cooperative models, J. Math. Biol., 2002, 45(3), 183-218. doi: 10.1007/s002850200145 [25] Z. Yu and R. Yuan, Travelling wave solutions in nonlocal reaction-diffusion systems with delays and applications, ANZIAM J., 2009, 51(1), 49-66. doi: 10.1017/S1446181109000406 [26] G. Zhang and X. Zhao, Propagation phenomena for a two-species Lotka-Volterra strong competition system with nonlocal dispersal, Calc. Var. Partial Differential Equations, 2020, 59(10), 34. doi: 10.1007/s00526-019-1662-5 -
-
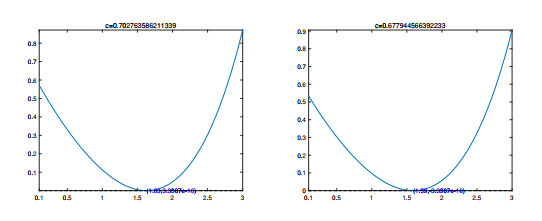
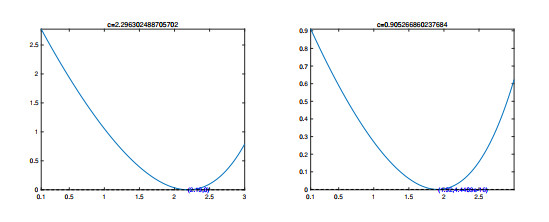
- Figure 1. Simulation of eigenvalue equations
-
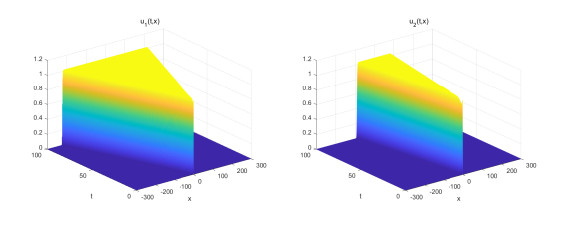
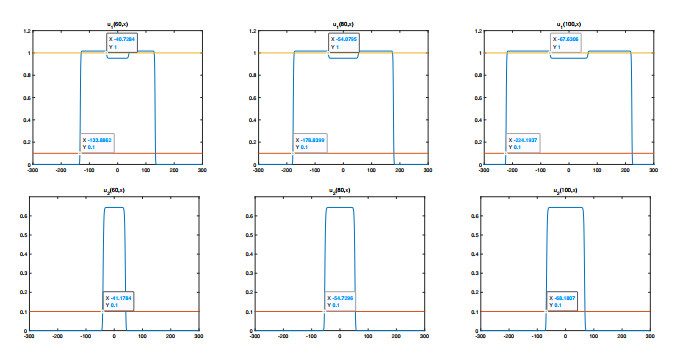
Figure 2. Spatial-temporal plots of
$ u_1, u_2 $ if$ a = b = 0 $ -
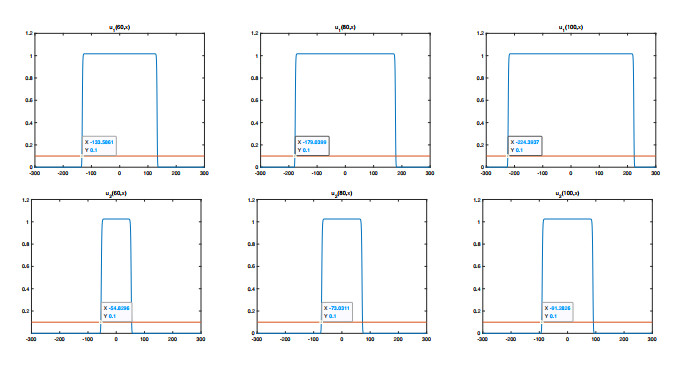
Figure 3. Level sets of
$ u_1, u_2 $ if$ a = b = 0 $ -
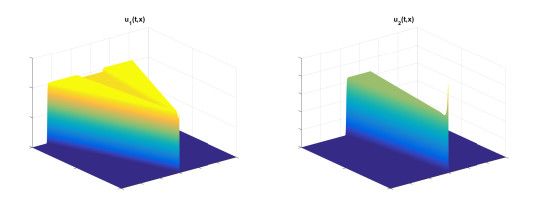
Figure 4. Spatial-temporal plots of
$ u_1, u_2 $ if$ a = 0.1, b = 0.4 $ - Figure 5. Simulation of eigenvalue equations
-
Figure 6. Level sets of
$ u_1, u_2 $ if$ a = 0.1, b = 0.4 $




 DownLoad:
DownLoad: