| Citation: |
Hai-Feng Huo, Li-Na Gu, Hong Xiang. MODELLING AND ANALYSIS OF AN HIV/AIDS MODEL WITH DIFFERENT WINDOW PERIOD AND TREATMENT[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1927-1950. doi: 10.11948/20200279
|
MODELLING AND ANALYSIS OF AN HIV/AIDS MODEL WITH DIFFERENT WINDOW PERIOD AND TREATMENT
-
Abstract
A novel HIV$ / $AIDS model with different window period and treatment is proposed. Window period individuals and latent individuals are divided into two types: treated and untreated in our model. The basic reproduction number $ R_{0} $ is obtained by using the next generation matrix. Stability of the disease-free equilibrium and existence of the endemic equilibrium is derived. Using the theory of central manifold, the generation of forward bifurcation is established. Existence of the optimal control pair is analyzed and the mathematical expression of the optimal control is also given by the Pontryagin maximum principle. The best-fit parameter values in our model are identified by the MCMC algorithm on the basis of the AIDS data in Gansu province of China from 2004 to 2019. We also estimate that the basic reproduction number $ R_{0} $ is $ 2.1985 $ (95%CI: (1.3535-3.0435)). Numerical simulation and sensitivity analysis of several parameters are also presented. Our results suggest that individuals who are in the stage of window period for AIDS should receive treatment, and this plays a key role in the prevention and control of HIV$ / $AIDS.
-
Keywords:
- Treatment /
- window period /
- forward bifurcation /
- optimal control
-
-
References
[1] National Bureau of Statistics of China (2019) Annual Statistics of Gansu Province, Available from: http://data.stats.gov.cn/. [2] Ten Facts about AIDS from the World Health Organization, Available from: https://www.who.int/features/factfiles/hiv/zh/. [3] World Health Organization fact sheet on AIDS, Available from: https://www.who.int/news-room/fact-sheets/detail/hiv-aids. [4] R. M. Anderson, The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS, Journal of Acquired Immune Deficiency Syndromes, 1988, 1(3), 241–256. [5] S. M. Blower and H. Dowlatabadi, Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example, International Statistical Review / Revue Internationale de Statistique, 1994, 62(2), 229. [6] M. P. Busch and G. A. Satten, Time course of viremia and antibody seroconversion following human immunodeficiency virus exposure, American Journal of Medicine, 1997, 102(5B), 117–24. [7] C. Castillo-Chavez and B. Song, Dynamical models of tuberculosis and their applications, Mathematical Biosciences and Engineering, 2004, 1(2), 361–401. doi: 10.3934/mbe.2004.1.361 [8] M. L. Chambers, The mathematical theory of optimal processes, Journal of the Operational Research Society, 1965, 16(4), 493–494. doi: 10.1057/jors.1965.92 [9] R. Coombs, Clinical laboratory diagnosis of HIV-1 and use of viral RNA to monitor infection, Sexually transmitted diseases, 4th ed. New York: McGrawHill, 2008, 1329–1347. [10] W. Fleming and R. W. Rishel, Deterministic and stochastic optimal control, Springer, Berlin, Germany, 1975. [11] I. Ghosh, P. K. Tiwari, S. Samanta and et al., A simple SI-type model for HIV/AIDS with media and self-imposed psychological fear, Mathematical Biosciences, 2018, 306, 160–169. doi: 10.1016/j.mbs.2018.09.014 [12] Z. K. Guo, H. F. Huo and H. Xiang, Hopf bifurcation of an age-structured HIV infection model with logistic target-cell growth, Journal of Biological Dynamics, 2019, 13(1), 362–384. doi: 10.1080/17513758.2019.1602171 [13] H. F. Huo, R. Chen and X. Y. Wang, Modelling and stability of HIV/AIDS epidemic model with treatment, Applied Mathematical Modelling, 2016, 40(13-14), 6550–6559. doi: 10.1016/j.apm.2016.01.054 [14] H. F. Huo and L. X. Feng, Global stability of an epidemic model with incomplete treatment and vaccination, Discrete Dynamics in Nature and Society, 2012, 3(13), 1–14. [15] H. F. Huo and L. X. Feng, Global stability for an HIV/AIDS epidemic model with different latent stages and treatment, Applied Mathematical Modelling, 2013, 37(3), 1480–1489. doi: 10.1016/j.apm.2012.04.013 [16] H. F. Huo, S. L. Jing, X. Y. Wang and et al., Modelling and analysis of an alcoholism model with treatment and effect of twitter, Mathematical Biosciences and Engineering, 2019, 16(5), 3595–3622. doi: 10.3934/mbe.2019179 [17] M. Kgosimore and E. M. Lungu, The effects of vertical transmission on the spread of HIV/AIDS in the presence of treatment, Mathematical Biosciences and Engineering, 2006, 3(2), 297–312. doi: 10.3934/mbe.2006.3.297 [18] M. Kot, Elements of mathematical biology, Cambridge University Press, Cambridge, 2001. [19] V. Lakshmikantham, S. Leela and A. A. Martynyuk, Stability analysis of nonlinear systems, Springer, 1989. [20] S. Lenhart and J. T. Workman, Optimal control applied to biological models, CRC press, 2007. [21] S. Marino, I. B. Hogue, C. J. Ray and et al., A methodology for performing global uncertainty and sensitivity analysis in systems biology, Journal of Theoretical Biology, 2008, 254(1), 178–196. doi: 10.1016/j.jtbi.2008.04.011 [22] R. M. May and R. M. Anderson, Transmission dynamics of HIV infection, Nature, 1987, 326(6109), 137–142. doi: 10.1038/326137a0 [23] S. H. Michaels, R. Clark and P. Kissinger, Declining morbidity and mortality among patients with advanced human immunodeficiency virus infection, New England Journal of Medicine, 1998, 339(6), 405–406. doi: 10.1056/NEJM199808063390612 [24] K. Nah, H. Nishiura, N. Tsuchiya and et al., Test-and-treat approach to HIV/AIDS: a primer for mathematical modeling, Theoretical Biology and Medical Modelling, 2017, 14(1), 16. doi: 10.1186/s12976-017-0062-9 [25] H. Nampala, L. S. Luboobi, J. Y. Mugisha and et al., Modelling hepatotoxicity and antiretroviral therapeutic effect in HIV/HBV coinfection, Mathematical Biosciences, 2018, 302, 67–79. doi: 10.1016/j.mbs.2018.05.012 [26] R. Naresh, A. Tripathi and S. Omar, Modelling the spread of AIDS epidemic with vertical transmission, Applied Mathematics and Computation, 2006, 178(2), 262–272. doi: 10.1016/j.amc.2005.11.041 [27] M. W. Shen, Y. N. Xiao, L. B. Rong and et al., Conflict and accord of optimal treatment strategies for HIV infection within and between hosts, Mathematical Biosciences, 2019, 309, 107–117. doi: 10.1016/j.mbs.2019.01.007 [28] R. J. Smith and S. M. Blower, Could disease-modifying HIV vaccines cause population-level perversity, The Lancet Infectious Diseases, 2004, 4(10), 636– 639. doi: 10.1016/S1473-3099(04)01148-X [29] Van den Driessche P and W. J, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, 2002, 180(1-2), 29–48. doi: 10.1016/S0025-5564(02)00108-6 [30] X. Wang, S. Y. Tang, X. Y. Song and et al., Mathematical analysis of an HIV latent infection model including both virus-to-cell infection and cell-to-cell transmission, Journal of Biological Dynamics, 2016, 11, 455–483. [31] M. J. Wawer, R. H. Gray, N. K. Sewankambo and et al., Rates of HIV-1 transmission per coital act, by stage of HIV-1 infection, in Rakai, Uganda, The Journal of Infectious Diseases, 2005, 191(9), 1403–1409. doi: 10.1086/429411 [32] Y. N. Xiao, S. Y. Tang, Y. C. Zhou and et al., Predicting the HIV/AIDS epidemic and measuring the effect of mobility in mainland China, Journal of Theoretical Biology, 2013, 317, 271–285. doi: 10.1016/j.jtbi.2012.09.037 [33] Y. P. Yang, Y. N. Xiao and J. H. Wu, Pulse HIV vaccination: Feasibility for virus eradication and optimal vaccination schedule, Bulletin of Mathematical Biology, 2013, 75(5), 725–751. doi: 10.1007/s11538-013-9831-8 [34] T. L. Zhang, M. H. Jia, H. B. Luo and et al., Study on a HIV/AIDS model with application to Yunnan province, China, Applied Mathematical Modelling, 2011, 35(9), 4379–4392. doi: 10.1016/j.apm.2011.03.004 [35] X. Y. Zhou, X. Y. Song and X. Y. Shi, Analysis of stability and hopf bifurcation for an HIV infection model with time delay, Applied Mathematics and Computation, 2008, 199(1), 23–38. doi: 10.1016/j.amc.2007.09.030 -
-
Figures(12) / Tables(2)
Export File
Citation
Hai-Feng Huo, Li-Na Gu, Hong Xiang. MODELLING AND ANALYSIS OF AN HIV/AIDS MODEL WITH DIFFERENT WINDOW PERIOD AND TREATMENT[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1927-1950. doi: 10.11948/20200279
Format
Content
DownLoad:
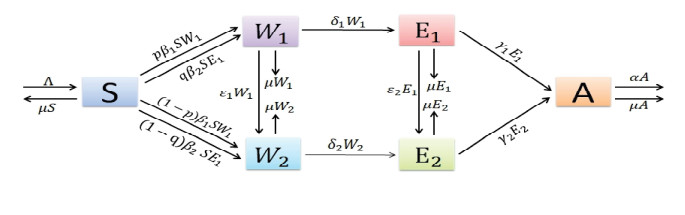
- Figure 1. Transfer diagram for the dynamics of HIV/AIDS.
-
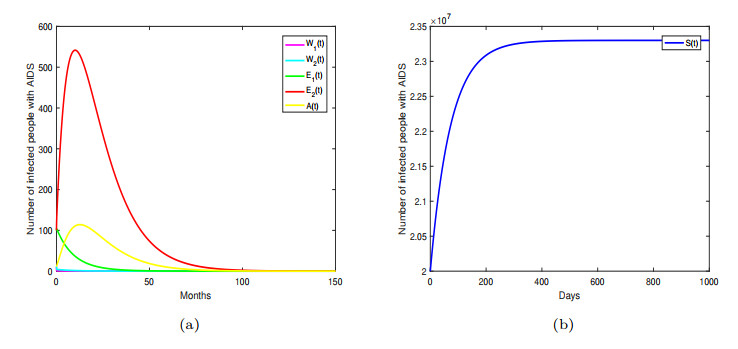
Figure 2. Disease free equilibrium
$ P_{0} $ is globally asymptotically stable. -
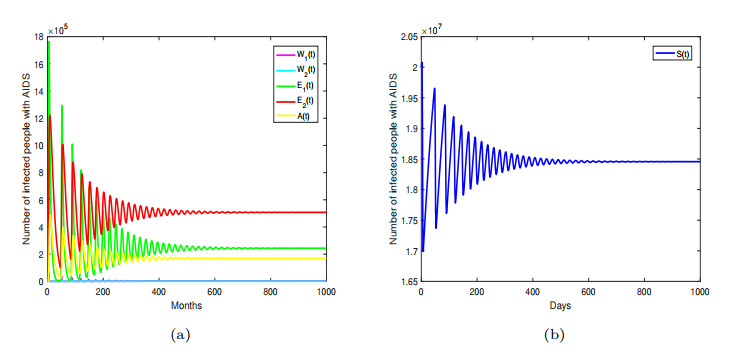
Figure 3. Endemic equilibrium
$ P^{*} $ is locally asymptotically stable. -
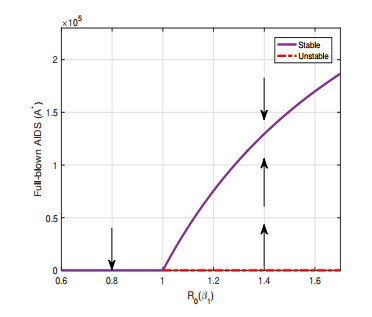
Figure 4. Illustration of forward bifurcation when one parameter
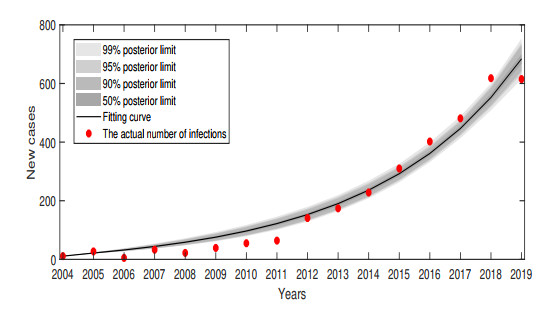
$ \beta_{1} $ in$ R_{0} $ is varied. - Figure 5. The actual number of people infected in Gansu Province from 2004 to 2019.
-
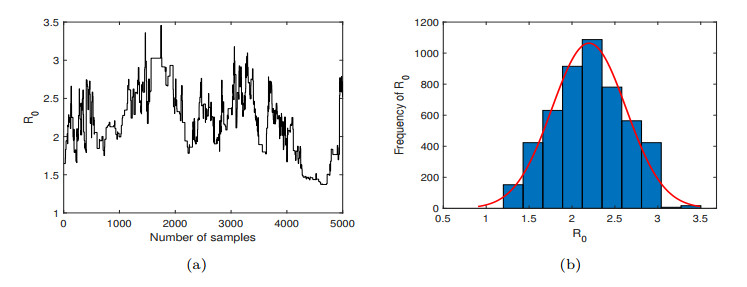
Figure 6. (a) The number of Markov chain samples of
$ R_{0} $ . The curve represents the size of the$ R_{0} $ value. (b) The frequency distribution of$ R_{0} $ . The red curve is the probability density function curve of$ R_{0} $ . -
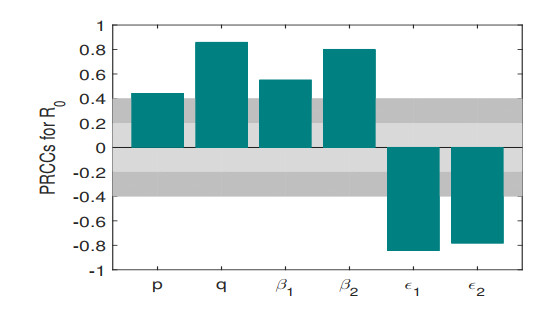
Figure 7. The Partial Rank Coefficients (PRCCs) of
$ R_{0} $ in system (2.1). -
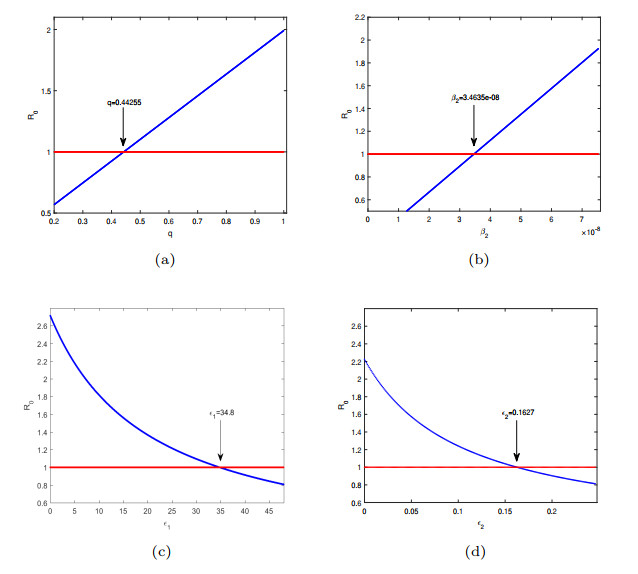
Figure 8. The variation trend between four parameters and the basic regeneration number
$ R_{0} $ . - Figure 9. The sensitivity of several parameters changes on infected individuals.
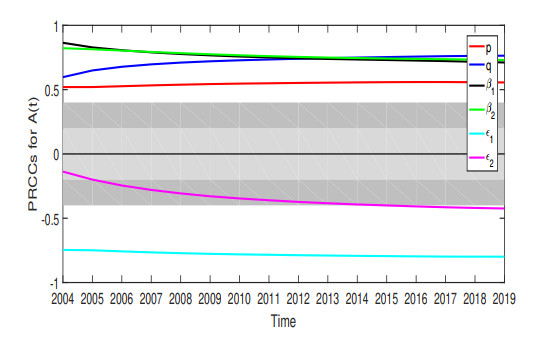
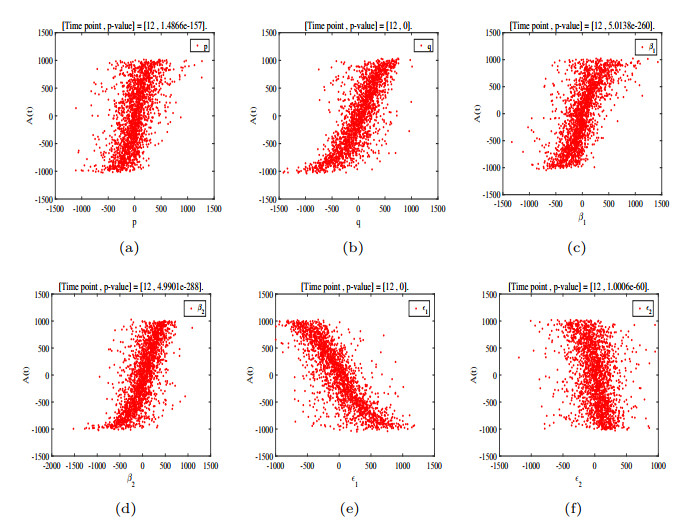
- Figure 10. P values of each parameter in the 12th year.
-
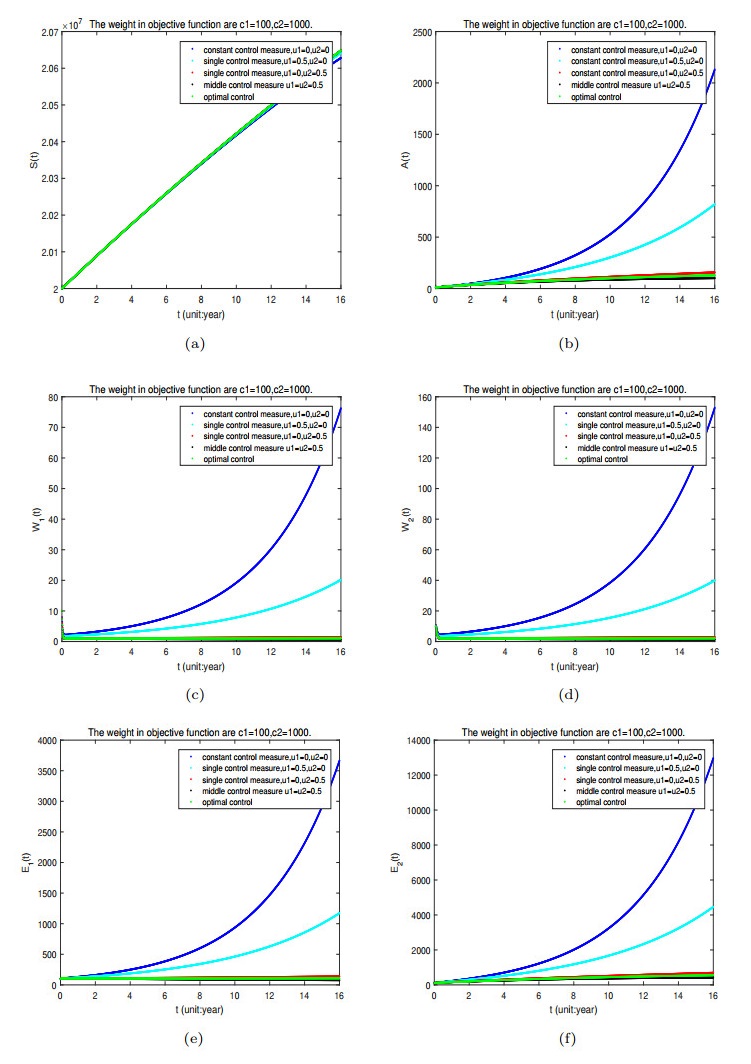
Figure 11. Number of people in different compartment when we select the weights on objective function are
$ c_{1} = 100; c_{2} = 1000 $ and under different optimal control strategies, that is, (1) without$ u_{1} = 0, u_{2} = 0 $ ; (2) single control$ u_{1} = 0.5, u_{2} = 0 $ ; (3) single control$ u_{1} = 0, u_{2} = 0.5 $ ; (4) middle control$ u_{1} = u_{2} = 0.5 $ ; (5) optimal control$ u_{1} = u_{1}^{*}, u_{2} = u_{2}^{*} $ . -
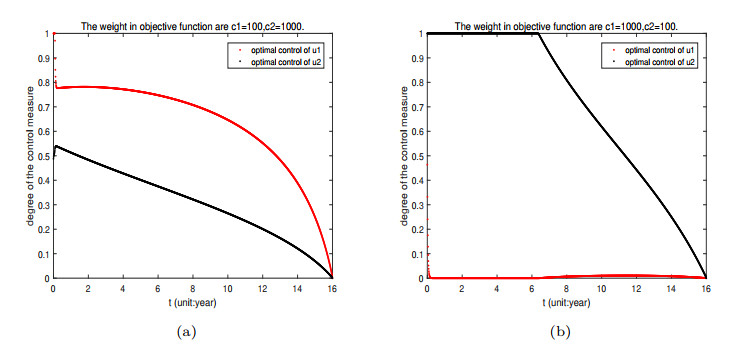
Figure 12. The impact of different weight coefficients on optimal control
$ u_{1}, u_{2} $ : (a)$ c_{1} = 100, c_{2} = 1000 $ ; (b)$ c_{1} = 1000, c_{2} = 100 $ .