| Citation: |
Ning Wang, Long Zhang, Zhidong Teng. A REACTION-DIFFUSION MODEL FOR NESTED WITHIN-HOST AND BETWEEN-HOST DYNAMICS IN AN ENVIRONMENTALLY-DRIVEN INFECTIOUS DISEASE[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1898-1926. doi: 10.11948/20200273
|
A REACTION-DIFFUSION MODEL FOR NESTED WITHIN-HOST AND BETWEEN-HOST DYNAMICS IN AN ENVIRONMENTALLY-DRIVEN INFECTIOUS DISEASE
-
Abstract
A reaction-diffusion model for nested within-host and between-host dynamics in an environmentally-driven infectious disease is proposed. The model is composed of the within-host virus infectious fast time model of ordinary differential equations and the between-host disease transmission slow time model of reaction-diffusion equations. The isolated fast model has been investigated in previous literature, and the main results are summarized. For the isolated slow model, the well-posedness of solutions, and the basic reproduction number $ R_{b} $ are obtained. When $ R_{b}\leq1 $, the model only has the disease-free equilibrium which is globally asymptotically stable, and when $ R_{b}>1 $ the model has a unique endemic equilibrium which is globally asymptotically stable. For the nested slow model, the positivity and boundedness of solutions, the basic reproduction number $ R_{c} $ and the existence of equilibrium are firstly obtained. Particularly, the nested slow model can exist two positive equilibrium when $ R_{c}<1 $ and a unique endemic equilibrium when $ R_{c}>1 $. When $ R_{c}<1 $ the disease-free equilibrium is locally asymptotically stable, and when $ R_{c}>1 $ and an additional condition is satisfied the unique endemic equilibrium is locally asymptotically stable. When there are two positive equilibria, then a positive equilibria is locally asymptotically stable under an additional condition and the other one is unstable, which implies that the nested slow model occurs the backward bifurcation at $ R_c = 1 $. Lastly, numerical examples are given to verify the main conclusions. The research shows that the nested slow model has more complex dynamical behavior than the corresponding isolated slow model.
-
-
References
[1] A. Alahmadi, S. Belet, A. Black, et al, Influencing public health policy with data-informed mathematical models of infectious diseases: Recent developments and new challenges, Epidemics, 2020, 32, 100393. doi: 10.1016/j.epidem.2020.100393 [2] N. D. Alikakos and G. Fusco, Entire solutions to equivariant elliptic systems with variational structure, Arch. Ration. Mech. Anal., 2011, 202(2), 567-597. doi: 10.1007/s00205-011-0441-z [3] L. J. S. Allen, B. M. Bolker, Y. Lou and A. L. Nevai, Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model, Disc. Cont. Dyn. Syst. Serie A., 2008, 21(1), 1-20. doi: 10.3934/dcds.2008.21.1 [4] R. Anguelov, J. Banasiak, C. Bright, et al, The big unknown: The asymptomatic spread of COVID-19, Biomath, 2020, 9(1), 1-9. [5] L. Arnold, C. K. Jones, K. Mischaikow and G. Raugel, Dynamical Systems. Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1995. [6] J. Bouhours and T. Giletti, Spreading and vanishing for a monostable reaction-diffusion equation with forced speed, J. Dyn. Diff. Equat., 2019, 31(1), 247-286. doi: 10.1007/s10884-018-9643-5 [7] X. Cen, Z. Feng and Y. Zhao, Emerging disease dynamics in a model coupling within-host and between-host systems, J. Theor. Biol., 2014, 361, 141-151. doi: 10.1016/j.jtbi.2014.07.030 [8] D. Coombs, M. A. Gilchrist and C. L. Ball, Evaluating the importance of within- and between-host selection pressures on the evolution of chronic pathogens, Theor. Popul. Biol., 2007, 72(4), 576-591. doi: 10.1016/j.tpb.2007.08.005 [9] R. Cui and Y. Lou, A spatial SIS model in advective heterogeneous environments, J. Diff. Eqs., 2016, 261(6), 3305-3343. doi: 10.1016/j.jde.2016.05.025 [10] J. Deen, M. A. Mengel and J. D. Clemens, Epidemiology of cholera, Vaccine, 2020, 38(Supplement 1), A31-A40. [11] Z. Feng, X. Cen, Y. Zhao and J. Velasco-Hernandez, Coupled within-host and between-host dynamics and evolution of virulence, Math. Biosci., 2015, 270(B), 204-212. [12] Z. Feng, J. Velasco-Hernandez and B. Tapia-Santos, A mathematical model for coupling within-host and between-host dynamics in an environmentally-driven infectious disease, Math. Biosci., 2013, 241(1), 49-55. doi: 10.1016/j.mbs.2012.09.004 [13] Z. Feng, J. Velasco-Hernandez, B. Tapia-Santos and M. C. A. Leite, A model for coupling within-host and between-host dynamics in an infectious disease, Nonlinear Dyn., 2012, 68(3), 401-411. doi: 10.1007/s11071-011-0291-0 [14] K. A. M. Gaythorpe, C. L. Trotter and A. J. K. Conlan, Modelling norovirus transmission and vaccination, Vaccine, 2018, 36(37), 5565-5571. doi: 10.1016/j.vaccine.2018.07.053 [15] M. A. Gilchrist and A. Sasaki, Modeling host-parasite coevolution: a nested approach based on mechanistic models, J. Theor. Biol., 2002, 218(3), 289-308. doi: 10.1006/jtbi.2002.3076 [16] J. Groeger, Divergence theorems and the supersphere, J. Geom. Phys., 2014, 77, 13-29. doi: 10.1016/j.geomphys.2013.11.004 [17] J. K. Hale, Asymptotic Behavior of Dissipative Systems, American Mathematical Society, Providence, RI, 1988. [18] K. Hattaf, N. Yousfi and A. Tridane, Mathematical analysis of a virus dynamics model with general incidence rate and cure rate, Nonlinear Anal. RWA., 2012, 13(4), 1866-1872. doi: 10.1016/j.nonrwa.2011.12.015 [19] D. Henry, Geometric Theory of Semilinear Parabolic Equations, Springer-Verlag, Berlin, 1981. [20] T. Kuniya and J. Wang, Lyapunov functions and global stability for a spatially diffusive SIR epidemic model, Appl. Anal., 2017, 96(11), 1935-1960. doi: 10.1080/00036811.2016.1199796 [21] Y. Lou and X. Zhao, A reaction-diffusion malaria model with incubation period in the vector population, J. Math. Biol., 2011, 62(4), 543-568. doi: 10.1007/s00285-010-0346-8 [22] J. Lu, Z. Teng and Y. Li, An age-structured model for coupling within-host and between-host dynamics in environmentally-driven infectious diseases, Chaos. Solitons. Fract., 2020, 139, 110024. doi: 10.1016/j.chaos.2020.110024 [23] Y. Luo, S. Tang, Z. Teng and L. Zhang, Global dynamics in a reaction-diffusion multi-group SIR epidemic model with nonlinear incidence, Nonlinear Anal. RWA., 2019, 50, 365-385. doi: 10.1016/j.nonrwa.2019.05.008 [24] Y. Luo, L. Zhang, T. Zheng and Z. Teng, Analysis of a diffusive virus infection model with humoral immunity, cell-to-cell transmission and nonlinear incidence, Physica A, 2019, 535, 122415. doi: 10.1016/j.physa.2019.122415 [25] Z. Ma, Y. Zhou and J. Wu, Modeling and Dynamics of Infectious Diseases, Higher Education Press, Beijing, 2009. [26] P. Magal, G. Webb and Y. Wu, On a vector-host epidemic model with spatial structure, Nonlinearity, 2018, 31(12), 5589-5614. doi: 10.1088/1361-6544/aae1e0 [27] R. Martin and H. L. Smith, Abstract functional-differential equations and reaction-diffusion systems, Trans. Am. Math. Soc., 1990, 321(1), 1-44. [28] H. Miao, X. Abdurahman, Z. Teng and L. Zhang, Dynamical analysis of a delayed reaction-diffusion virus infection model with logistic growth and humoral immune impairment, Chaos. Solitons. Fract., 2018, 110, 280-291. doi: 10.1016/j.chaos.2018.03.006 [29] H. Miao, Z. Teng, X. Abdurahman and Z. Li, Global stability of a diffusive and delayed virus infection model with general incidence function and adaptive immune response, Comput. Appl. Math., 2018, 37(3), 3780-3805. doi: 10.1007/s40314-017-0543-9 [30] N. Mideo, S. Alizon and T. Day, Linking within- and between-host dynamics in the evolutionary epidemiology of infectious diseases, Trends Ecol. Evol., 2008, 23(9), 511-517. doi: 10.1016/j.tree.2008.05.009 [31] K. A. Murray, N. Preston, T. Allen, et al, Global biogeography of human infectious diseases, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(41), 12746-12751. doi: 10.1073/pnas.1507442112 [32] A. Naheed, A study of spatio-temporal spread of infectious disease: SARS, Bull. Aust. Math. Soc., 2016, 94(3), 522-523. doi: 10.1017/S0004972716000484 [33] L. Nelli, H. M. Ferguson and J. Matthiopoulos, Achieving explanatory depth and spatial breadth in infectious disease modelling: Integrating active and passive case surveillance, Stat. Methods Med. Res., 2019, 29(5), 1273-1287. [34] J. Rosenthal, Climate change and the geographic distribution of infectious diseases, EcoHealth, 2009, 6(4), 489-495. doi: 10.1007/s10393-010-0314-1 [35] M. Tahir, S. Shah, G. Zaman and T. Khan, Stability behaviour of mathematical model MERS corona virus spread in population, Filomat, 2019, 33(12), 3947-3960. doi: 10.2298/FIL1912947T [36] S. Tang, Z. Teng and H. Miao, Global dynamics of a reaction-diffusion virus infection model with humoral immunity and nonlinear incidence, Comput. Math. Appl., 2019, 78(3), 786-806. doi: 10.1016/j.camwa.2019.03.004 [37] Y. Tian and X. Liu, Global dynamics of a virus dynamical model with general incidence rate and cure rate, Nonlinear Anal. RWA., 2014, 16(1), 17-26. [38] F. Van den Bosch, J. A. J. Metz and O. Diekmann, The velocity of spatial population expansion, J. Math. Biol., 1990, 28, 529-565. doi: 10.1007/BF00164162 [39] B. Wen, J. Wang and Z. Teng, A discrete-time analog for coupled within-host and between-host dynamics in environmentally driven infectious disease, Adv. Diff. Equat., 2018, 2018(1), 69. doi: 10.1186/s13662-018-1522-1 [40] J. Wu, Theory and Applications of Partial Functional Differential Equations, Springer-Verlag, New York, 1996. [41] Y. Wu and X. Zou, Asymptotic profiles of steady states for a diffusive SIS epidemic model with mass action infection mechanism, J. Diff. Eqs., 2016, 261(8), 4424-4447. doi: 10.1016/j.jde.2016.06.028 [42] Q. Ye, Z. Li, M. Wang and Y. Wu, Introduction to Reaction-Diffusion Equations (In Chinese), Science Press, 2th edition, Beijing, 2011. [43] Y. Yuan and Z. Guo, Monotone methods and stability results for nonlocal reaction-diffusion equations with time delay, J. Appl. Anal. Comput., 2018, 8(5), 1342-1368. -
-
Figures(7)
Export File
Citation
Ning Wang, Long Zhang, Zhidong Teng. A REACTION-DIFFUSION MODEL FOR NESTED WITHIN-HOST AND BETWEEN-HOST DYNAMICS IN AN ENVIRONMENTALLY-DRIVEN INFECTIOUS DISEASE[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1898-1926. doi: 10.11948/20200273
Format
Content
DownLoad:
-
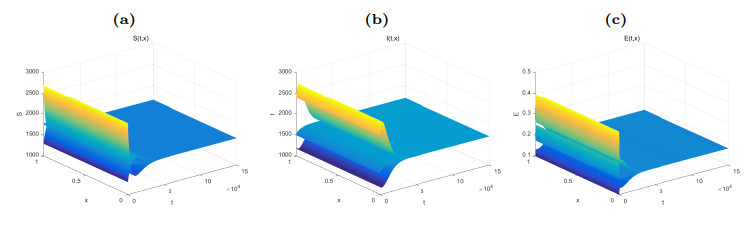
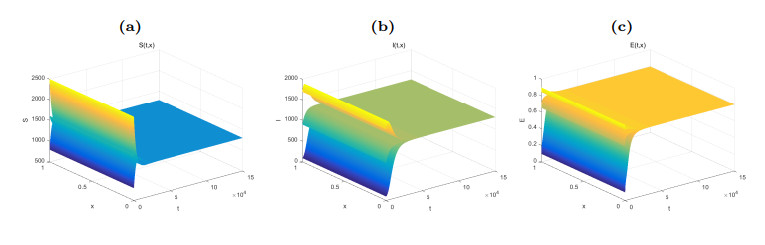
Figure 1. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W} $ . -
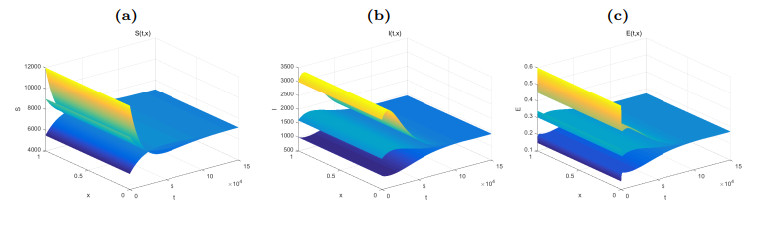
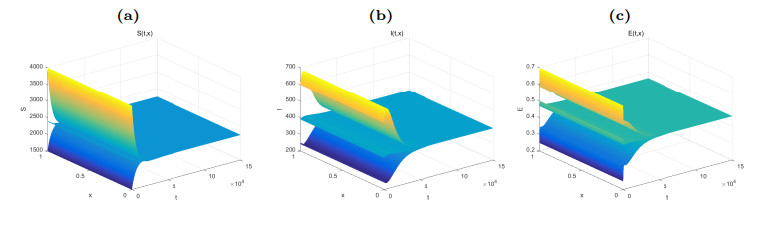
Figure 2. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W} $ . -
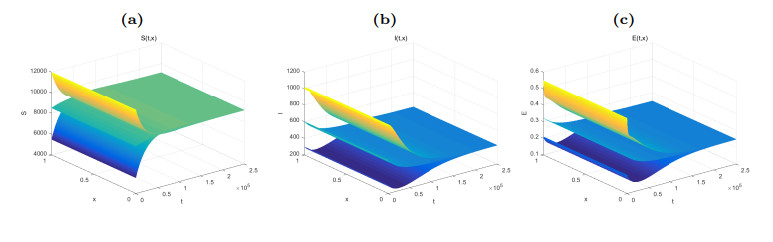
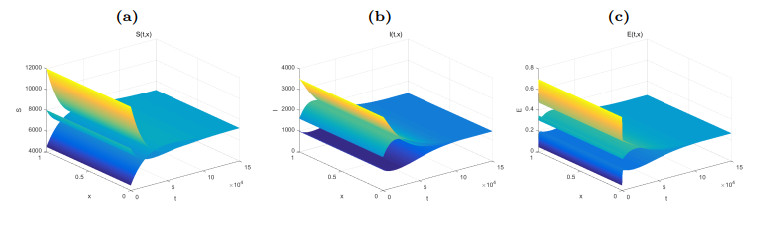
Figure 3. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W} $ . -
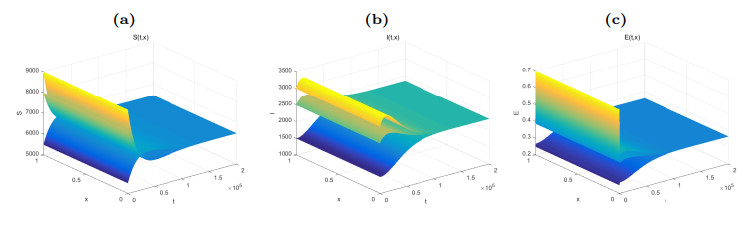
Figure 4. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W} $ . -
Figure 5. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W} $ . -
Figure 6. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W}_{2} $ . -
Figure 7. Dynamical behaviors of
$ S(t, x) $ (Fig. (a)),$ I(t, x) $ (Fig. (b)) and$ E(t, x) $ (Fig. (c)). The numerical simulations indicate that the solutions finally converge to the equilibrium$ \widetilde{W}_{2} $ .