| Citation: | Jing Ge, Zhigui Lin, Huaiping Zhu. MODELING THE SPREAD OF WEST NILE VIRUS IN A SPATIALLY HETEROGENEOUS AND ADVECTIVE ENVIRONMENT[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1868-1897. doi: 10.11948/20200258 |
MODELING THE SPREAD OF WEST NILE VIRUS IN A SPATIALLY HETEROGENEOUS AND ADVECTIVE ENVIRONMENT
-
Abstract
In this paper, we put forward and explore a reaction-diffusion-advection system with free boundaries in spatially heterogeneous environment to model the spatial transmission of West Nile virus. The transmission dynamics are given for the model involving mosquitoes and birds, and the free boundaries are introduced to describe the moving fronts of the infected region. The spatial-temporal risk index $ R_0^F(t) $, which depends on time $ t $, spatial heterogeneity and advection intensity, is derived by variational method. Sufficient conditions for the virus to extinct or to persist are given. Our results show that, if $ R^F_0(\infty)\leq 1 $, the virus extinct eventually, and if $ R^F_0(t_0)\geq 1 $ for some $ t_0\geq 0 $, the virus will spread continuously, while if $ R^F_0(0)<1<R^F_0(\infty) $, the extinction or persistence of the virus depends on the initial scale of infected mosquitoes and birds, or the size of the infected region, the advection intensity and other factors. Finally, numerical simulations indicate that the advection intensity and the expanding capability affect the spreading fronts of the infected region.
-
Keywords:
- West Nile virus /
- heterogeneity /
- advection /
- free boundary /
- the risk index
-

-
References
[1] A. Abdelrazec, S. Lenhart and H. Zhu, Transmission dynamics of West Nile virus in mosquitoes and corvids and non-corvids, J. Math. Biol., 2014, 68, 1553-1582. doi: 10.1007/s00285-013-0677-3 [2] I. Ahn, S. Baek and Z. Lin, The spreading fronts of an infective environment in a man-environment-man epidemic model, Appl. Math. Model., 2016, 40, 7082-7101. doi: 10.1016/j.apm.2016.02.038 [3] L. J. S. Allen, B. M. Bolker, Y. Lou and A. L. Nevai, Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model, Discrete Contin. Dyn. Syst. Ser. A, 2008, 21, 1-20. doi: 10.3934/dcds.2008.21.1 [4] Anopheles Mosquitoes, Centers for Disease Control and Prevention, http://www.cdc.gov/malaria/about/biology/mosquitoes/. Accessed: May, 2016. [5] Z. Bai, R. Peng and X. Zhao, A reaction-diffusion malaria model with seasonality and incubation period, J. Math. Biol., 2018, 77, 201-228. doi: 10.1007/s00285-017-1193-7 [6] W. Bao, Y. Du, Z. Lin, and H. Zhu, Free boundary models for mosquito range movement driven by climate warming, J. Math. Biol., 2018, 76, 841-875. doi: 10.1007/s00285-017-1159-9 [7] C. Bowman, A. B. Gumel, J. Wu, P. van den Driessche and H. Zhu, A mathematical model for assessing control strategies against West Nile virus, Bull. Math. Biol., 2005, 67, 1107-1133. doi: 10.1016/j.bulm.2005.01.002 [8] S. Bhowmick, J. Gethmann, F. J. Conraths, I. M. Sokolov, H. H. Lentz and H. K. Hartmut, Locally temperature-driven mathematical model of West Nile virus spread in Germany, J. Theoret. Biol., 2020, 488, 110117, 12 pp. doi: 10.1016/j.jtbi.2019.110117 [9] G. L. Campbell, A. A. Marfin, R. S. Lanciotti and D. J. Gubler, West Nile virus, The Lancet infectious diseases, 2002, 2(9), 519-529. doi: 10.1016/S1473-3099(02)00368-7 [10] R. S. Cantrell and C. Cosner, Spatial Ecology via Reaction-Diffusion Equations, John Wiley and Sons Ltd., Chichester, UK, 2003. [11] L. F. Chaves, G. L. Hamer, E. D. Walker, W. M. Brown, M. O. Ruiz and U. D. Kitron, Climatic variability and landscape heterogeneity impact urban mosquito diversity and vector abundance and infection, Ecosphere, 2011, 2(6), 1-21. [12] Centers for Diseases Control and Prevention, West Nile Virus: Preliminary Maps & Data for 2014, http://www.cdc.gov/westnile/statsMaps/preliminaryMapsData/index.html. [13] R. Cui and Y. Lou, A spatial SIS model in advective heterogeneous environments, J. Differential Equations, 2016, 261, 3305-3343. doi: 10.1016/j.jde.2016.05.025 [14] Y. Du and Z. Lin, Spreading-vanishing dichotomy in the diffusive logistic model with a free boundary, SIAM J. Math. Anal., 2010, 42, 377-405. doi: 10.1137/090771089 [15] P. van den Driessche and J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 2002, 180, 29-48. doi: 10.1016/S0025-5564(02)00108-6 [16] J. Ge, K. I. Kim, Z. Lin and H. Zhu, A SIS reaction-diffusion-advection model in a low-risk and high-risk domain, J. Differential Equations, 2015, 259, 5486-5509. doi: 10.1016/j.jde.2015.06.035 [17] J. Ge, C. Lei and Z. Lin, Reproduction numbers and the expanding fronts for a diffusionšCadvection SIS model in heterogeneous time-periodic environment, Nonlinear Anal. Real World Appl., 2017, 33, 100-120. doi: 10.1016/j.nonrwa.2016.06.005 [18] L. C. Harrington, T. W. Scott, K. Lerdthusnee, R. C. Coleman, A. Costero, G. G. Clarck, J. J. Jones, S. Kitthawee, P. K. Yapong, R. Sithiprasasna and J. D. Edman, Dispersal of the dengue vector Aedes aegypti within and between rural communities, American Journal of Tropical Medicine and Hygiene, 2005, 72, 209-220. doi: 10.4269/ajtmh.2005.72.209 [19] H. Huang and M. Wang, The reaction-diffusion system for an SIR epidemic model with a free boundary, Discrete Contin. Dyn. Syst. Ser. B, 2015, 20, 2039-2050. [20] V. M. Kenkre, R. R. Parmenter, I. D. Peixoto and L. Sadasiv, A theoretical framework for the analysis of the West Nile Virus epidemic, Comput. Math. Appl., 2005, 42, 313-324. [21] K. Kousuke, H. Matsuzawa and R. Peng, Concentration profile of endemic equilibrium of a reaction-diffusion-advection SIS epidemic model, Calc. Var. Partial Differential Equations, 2017, 56, Art. 112, 28 pp. doi: 10.1007/s00526-017-1207-8 [22] M. A. Lewis, J. Renclawowicz and P. van den Driessche, Traveling waves and spread rates for a West Nile virus model, Bull. Math. Biol., 2006, 68(1), 3-23. doi: 10.1007/s11538-005-9018-z [23] C. Lei, J. Xiong and X. Zhou, Qualitative analysis on an SIS epidemic reaction-diffusion model with mass action infection mechanism and spontaneous infection in a heterogeneous environment, Discrete Contin. Dyn. Syst. Ser. B, 2020, 25, 81-98. [24] F. Li, J. Liu and X. Zhao, A West Nile virus model with vertical transmission and periodic time delays, J. Nonlinear Sci., 2020, 30, 449-486. doi: 10.1007/s00332-019-09579-8 [25] H. Li, R. Peng and F. Wang, Varying total population enhances disease persistence: Qualitative analysis on a diffusive SIS epidemic model, J. Differential Equations, 2017, 262, 885-913. doi: 10.1016/j.jde.2016.09.044 [26] H. Li, R. Peng and T. Xiang, Dynamics and asymptotic profiles of endemic equilibrium for two frequency-dependent SIS epidemic models with cross-diffusion, European J. Appl. Math., 2020, 31, 26-56. doi: 10.1017/S0956792518000463 [27] G. M. Lieberman, Second Order Parabolic Differential Equations, World Scientific Publishing Co. Inc., River Edge, NJ, 1996. [28] H. Lin and F. Wang, Global dynamics of a nonlocal reaction-diffusion system modeling the West Nile virus transmission, Nonlinear Anal. Real World Appl., 2019, 46, 352-373. doi: 10.1016/j.nonrwa.2018.09.021 [29] Z. Lin and H. Zhu, Spatial spreading model and dynamics of West Nile virus in birds and mosquitoes with free boundary, J. Math. Biol., 2017, 75(6-7), 1381-1409. doi: 10.1007/s00285-017-1124-7 [30] R. Liu, J. Shuai, J. Wu and H. Zhu, Modeling spatial spread of West Nile virus and impact of directional dispersal of birds, Math. Biosci. Eng., 2006, 3, 145-160. doi: 10.3934/mbe.2006.3.145 [31] N. A. Maidana and H. Yang, Spatial spreading of West Nile virus described by traveling waves, J. Theoret. Biol., 2009, 258, 403-417. doi: 10.1016/j.jtbi.2008.12.032 [32] R. Peng, Asymptotic profile of the positive steady state for an SIS epidemic reaction-diffusion model, I. , J. Differential Equations, 2009, 247, 1096-1119. doi: 10.1016/j.jde.2009.05.002 [33] Z. Qiu, X. Wei, C. Shan and H. Zhu, Monotone dynamics and global behaviors of a West Nile virus model with mosquito demographics, J. Math. Biol., 2020, 80, 809-834. doi: 10.1007/s00285-019-01442-4 [34] H. L. Smith, Monotone Dynamical Systems, American Math. Soc., Providence, 1995. [35] M. Wang, A diffusive logistic equation with a free boundary and sign-changing coefficient in time-periodic environment, J. Funct. Anal., 2016, 270, 483-508. doi: 10.1016/j.jfa.2015.10.014 [36] W. Wang and X. Zhao, Basic reproduction numbers for reaction-diffusion epidemic models, SIAM J. Appl. Dyn. Syst., 2012, 11, 1652-1673. doi: 10.1137/120872942 [37] Y. Wu and X. Zou, Asymptotic profiles of steady states for a diffusive SIS epidemic model with mass action infection mechanism, J. Differential Equations, 2016, 261, 4424-4447. doi: 10.1016/j.jde.2016.06.028 [38] G. Wang, R. B. Minnis, J. L. Belant, and C. L. Wax, Dry weather induces outbreaks of human West Nile virus infections, BMC infectious diseases, 2010, 38, 1-7. [39] M. Wang, A diffusive logistic equation with a free boundary and sign-changing coefficient in time-periodic environment, J. Funct. Anal., 2016, 270, 483-508. doi: 10.1016/j.jfa.2015.10.014 [40] J. Zhang, C. Cosner and H. Zhu, Two-patch model for the spread of West Nile virus, Bull. Math. Biol., 2018, 80, 840-863. doi: 10.1007/s11538-018-0404-8 -
-
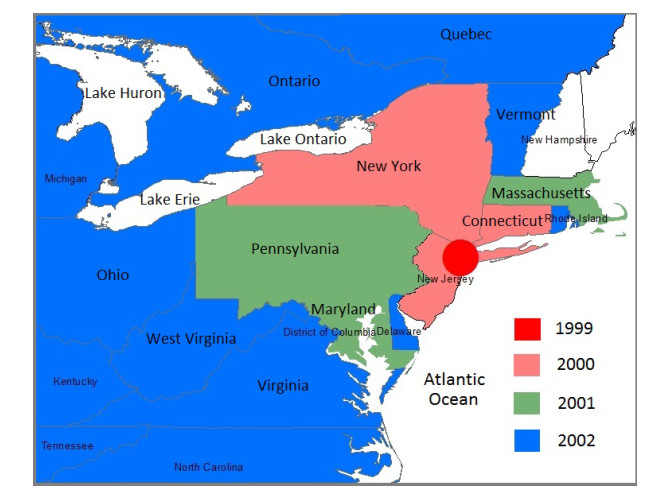
- Figure 1. The diffusion and advection movements of West Nile virus from New York city to its neighboring states from 1999 to 2002.
-
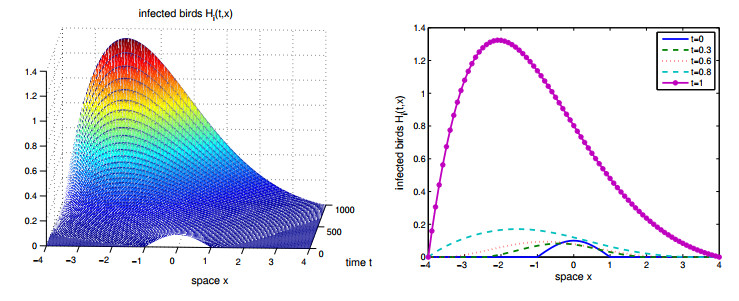
Figure 2.
$ \mu = 0.4 $ and$ \beta = 0.0008 $ . The solution$ H_i(t, x) $ turns left and stabilizes to a positive equilibrium. -
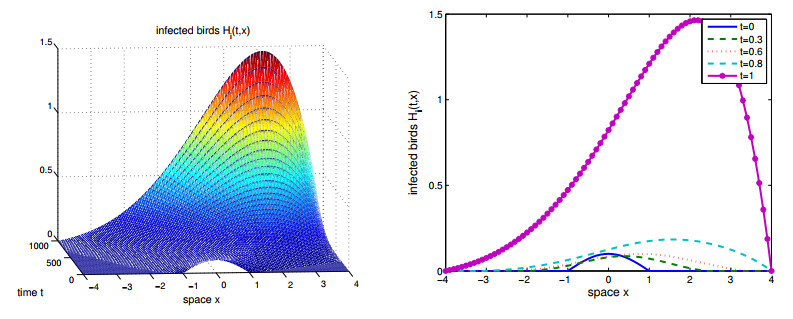
Figure 3.
$ \mu = 0.4 $ and$ \beta = -0.0008 $ . The solution$ H_i(t, x) $ turns right and stabilizes to a steady state solution. -
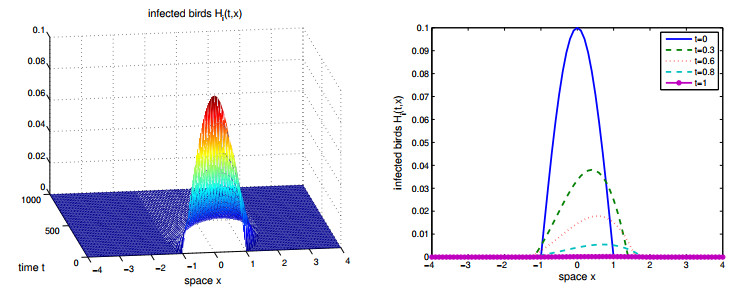
Figure 4.
$ \beta = -0.009 $ and$ \mu = 0.05 $ . The solution$ H_i(t, x) $ decays to zero quickly and the free boundaries increase slowly.




 DownLoad:
DownLoad: