| Citation: | Yuhao Cong, Zheng Wang. STATIC OUTPUT FEEDBACK DESIGN USING MODEL REDUCTION METHODS FOR SECOND-ORDER SYSTEMS[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1852-1867. doi: 10.11948/20200241 |
STATIC OUTPUT FEEDBACK DESIGN USING MODEL REDUCTION METHODS FOR SECOND-ORDER SYSTEMS
-
Abstract
In this paper, the static output feedback design is investigated using model reduction methods for large-scale second-order systems. First, based on the second-order Krylov subspace method, a low dimensional structure-preserving second-order system is derived. Then, applying matrix transformation, the relationship between input variables and output variables is directly established in the low dimensional system. We design output feedback controller for this system. Finally, using the argument principle, a computable stability criterion is presented to check the stability of the closed-loop system. Furthermore, a numerical algorithm is provided to design the output feedback controller for large-scale second-order systems. Numerical examples are given to illustrate the effectiveness of the algorithms.
-

-
References
[1] T. H. S. Abdelaziz, Robust pole placement for second-order linear systems using velocity-plus-acceleration feedback, IET Control Theory Appl., 2013, 7(14), 1843-1856. doi: 10.1049/iet-cta.2013.0039 [2] T. H. S. Abdelaziz and M. Valášek, Eigenstructure assignment by proportional-plus-derivative feedback for second-order linear control systems, Kybernetika, 2005, 41(5), 661-676. [3] F. D. Adegas and J. Stoustrup, Linear matrix inequalities for analysis and control of linear vector second-order systems, Int. J. Robust Nonlinear Control, 2015, 25(16), 2939-2964. doi: 10.1002/rnc.3242 [4] A. C. Antoulas, Approximation of large-scale dynamical systems, SIAM, Philadelphia, 2005. [5] Z. Bai and Y. Su, SOAR: A second-order Arnoldi method for the solution of the quadratic eigenvalue problem, SIAM J. Matrix Anal. Appl., 2005, 26(3), 640-659. doi: 10.1137/S0895479803438523 [6] Z. Bai and Y. Su, Dimension reduction of large-scale second-order dynamical systems via a second-order Arnoldi method, SIAM J. Sci. Comput., 2005, 26(5), 1692-1709. doi: 10.1137/040605552 [7] P. Benner, M. Hinze and E. Ter Maten, eds., Model reduction for circuit simulation, Lecture notes in electrical engineering, 74, Springer-Verlag, Dordrecht, 2011. [8] P. Benner, V. Mehrmann and D. C. Sorensen, eds., Dimension reduction of large-scale systems, Lecture Notes in Computational Science and Engineering, 45, Springer-Verlarg, Berlin, Heidelberg, 2005. [9] P. Benner, M. Ohlberger, A. Cohen and K. Willcox, Model reduction and approximation: theory and algorithms, SIAM, Philadelphia, 2017. [10] J. W. Brown and R. V. Churchill, Complex variables and applications, McGraw-Hill, New York, 2014. [11] Y. Chahlaoui, D. Lemonnier, A. Vandendorpe and P. Van Dooren, Second-order balanced truncation, Linear Algebra Appl., 2006, 415, 373-384. doi: 10.1016/j.laa.2004.03.032 [12] R. R. Craig and A. J. Kurdila, Fundamentals of structural dynamics, John Wiley & Sons, Hoboken, 2006. [13] E. Fosong, P. Schulze and B. Unger, From time-domain data to low-dimensional structured models, arXiv: 1902.05112v1, 2019. [14] R. Galindo, Stabilisation of matrix polynomials, Int. J. Control, 2015, 88(10), 1925-1932. doi: 10.1080/00207179.2015.1012651 [15] W. Gawronski, Advanced structural dynamics and active control of structures, Springer-Verlag, New York, 2004. [16] C. Gu, Matrix Padé-type approximant and directional matrix Padé approximant in the inner product space, J. Comput. Appl. Math., 2004, 164-165(1), 365-385. [17] J. Han, E. B. Rudnyi and J. G. Korvink, Efficient optimization of transient dynamic problems in MEMS devices using model order reduction, J. Micromech. Microeng., 2005, 15(4), 822-832. doi: 10.1088/0960-1317/15/4/021 [18] C. Hartmann, V. Wheeler and C. Schütte, Balanced truncation of linear second-order systems: a Hamiltonian approach, Multiscale Model. Simul., 2010, 8(4), 1348-1367. doi: 10.1137/080732717 [19] G. Hu and X. Hu, Stability criteria of matrix polynomials, Int. J. Control, 2019, 92(12), 2973-2978. doi: 10.1080/00207179.2018.1467045 [20] Y. Lin, L. Bao and Y. Wei, Model-order reduction of large-scale second-order MIMO dynamical systems via a block second-order Arnoldi method, Int. J. Comput. Math., 2007, 84(7), 1003-1019. doi: 10.1080/00207160701253836 [21] S. E. Lyshevski, MEMS and NEMS: systems, devices, and structures, CRC Press, New York, 2002. [22] N. K. Nichols and J. Kautsky, Robust eigenstructure assignment in quadratic matrix polynomials: nonsingular case, SIAM J. Matrix Anal. Appl., 2001, 23(1), 77-102. doi: 10.1137/S0895479899362867 [23] P. J. Rabier and W. C. Rheinboldt, Nonholonomic motion of rigid mechanical systems from a DAE viewpoint, SIAM, Philadelphia, 2000. [24] B. Salimbahrami and B. Lohmann, Order reduction of large scale second-order systems using Krylov subspace methods, Linear Algebra Appl., 2006, 415, 385-405. doi: 10.1016/j.laa.2004.12.013 [25] S. D. Senturia, N. Aluru and J. White, Simulating the behavior of MEMS devices: computational methods and needs, IEEE Comput. Sci. Engrg., 1997, 4(1), 30-43. doi: 10.1109/99.590854 [26] K. K. Stavrakakis, Model order reduction methods for parameterized systems in electromagnetic field simulations, Ph. D. thesis, Technische Universität, 2012. [27] Z. Tomljanović, C. Beattie and S. Gugercin, Damping optimization of parameter dependent mechanical systems by rational interpolation, Adv. Comput. Math., 2018, 44, 1797-1820. doi: 10.1007/s10444-018-9605-9 [28] Z. Xiao, Y. Jiang and Z. Qi, Structure preserving balanced proper orthogonal decomposition for second-order form systems via shifted Legendre polynomials, IET Control Theory Appl., 2019, 13(8), 1155-1165. doi: 10.1049/iet-cta.2018.5946 [29] F. Zhang, Matrix theory: basic results and techniques, Springer, New York, 2011. [30] L. Zhang, G. Zhang and W. Liu, Optimal control of second-order and high-order descriptor systems, Optim. Control Appl. Methods, 2019, 40(4), 791-806. doi: 10.1002/oca.2511 -
-
-
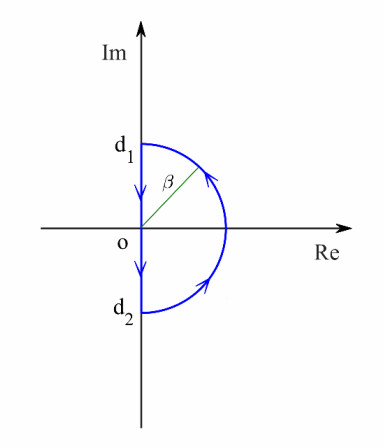
Figure 1. Region
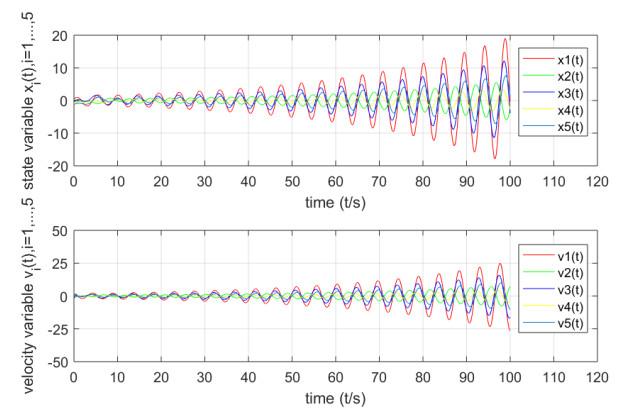
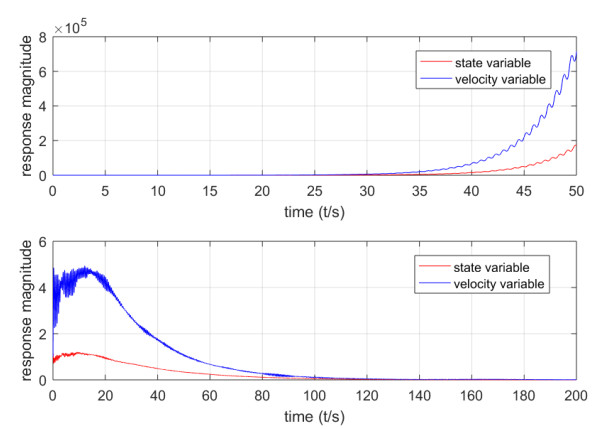
$ \Omega $ - Figure 2. The state response of the original system in Example 5.1
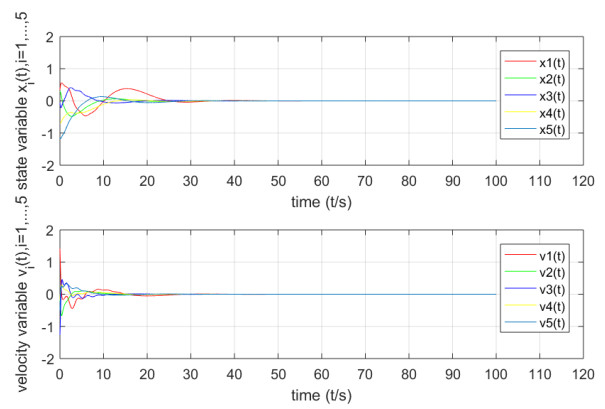
- Figure 3. The state response of the closed-loop system in Example 5.1
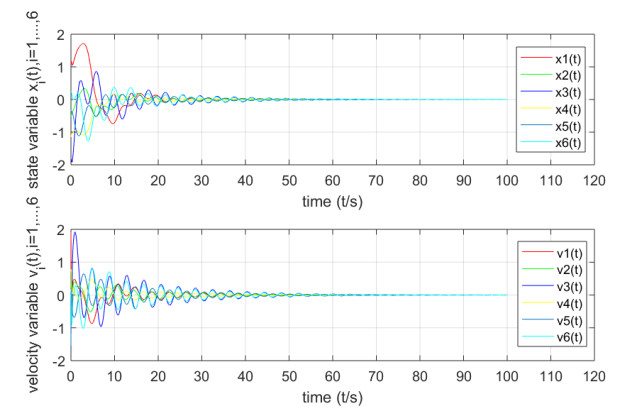
- Figure 4. The state response of the closed-loop system by Riccati equation method in Example 5.2
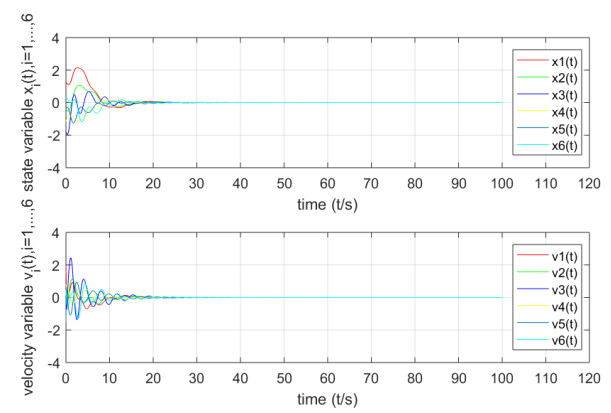
- Figure 5. The state response of the closed-loop system in Example 5.2
- Figure 6. The state responses of the original system and closed-loop system in Example 5.3




 DownLoad:
DownLoad: