| Citation: |
Chun-Bo Lian, Gang-Ling Hou, Bin Ge, Kang Zhou. MULTI-CLUSTER FLOCKING BEHAVIOR FOR A CLASS OF CUCKER-SMALE MODEL WITH A PERTURBATION[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1825-1851. doi: 10.11948/20200234
|
MULTI-CLUSTER FLOCKING BEHAVIOR FOR A CLASS OF CUCKER-SMALE MODEL WITH A PERTURBATION
-
Abstract
In this paper, we study a Cucker-Smale-type system with a perturbation in which agents interact with each other by given communication weights. By using a Lyapunov functional approach and some induction arguments we will prove that every agent flocks to the leader, and the flocking of the model depends on the perturbed conditions and initial conditions. Finally, we also provide several numerical examples and compare them with analytical results.
-
Keywords:
- Flocking behavior /
- perturbation /
- leader /
- Cucker-Smale model
-
-
References
[1] S. Ahn, H. Choi, S. Y. Ha and H. Lee, On collision-avoiding initial configurations to Cucker-Smale type flocking models, Commun. Math. Sci., 2012, 10(2), 625-643. doi: 10.4310/CMS.2012.v10.n2.a10 [2] S. Ahn, H. O. Bae, S. Y. Ha, Y. Kim and H. Lim, Application of flocking mechanism to the modeling of stochastic volatility, Math. Models Methods Appl. Sci., 2013, 23(9), 1603-1628. doi: 10.1142/S0218202513500176 [3] F. Cucker and S. Smale, Emergent behavior in flocks, IEEE Trans. Autom. Control, 2007, 52(5), 852-862. doi: 10.1109/TAC.2007.895842 [4] F. Cucker and S. Smale, On the mathematics of emergence, Jpn. J. Math., 2007, 2(1), 197-227. doi: 10.1007/s11537-007-0647-x [5] F. Cucker and E. Mordecki, Flocking in noisy environments, J. Math. Pure Appl., 2008, 89(3), 278-296. doi: 10.1016/j.matpur.2007.12.002 [6] J. Carrillo, M. Fornasier, J. Rosado and G. Toscani, Asymptotic flocking dynamics for the kinetic Cucker-Smale model, SIAM J. Math. Anal., 2010, 42(1), 218-236. doi: 10.1137/090757290 [7] J. Canizo, J. Carrillo and J. Rosado, A well-posedness theory in measures for some kinetic models of collective motion, Math. Models Methods Appl. Sci., 2011, 21(3), 515-539. doi: 10.1142/S0218202511005131 [8] F. Cucker and J. Dong, A general collision-avoiding flocking framework, IEEE Trans. Automat. Control, 2011, 56(5), 1124-1129. doi: 10.1109/TAC.2011.2107113 [9] J. Cho, S. Y. Ha, F. Huang, C. Jin and D. Ko, Emergence of bi-cluster flocking for the Cucker-Smale model, Math. Models Methods Appl. Sci., 2016, 26(6), 1191-1218. doi: 10.1142/S0218202516500287 [10] Y. P. Choi and J. Haskovec, Cucker-Smale model with normalized communication weights and time delay, Kinet. Relat. Models, 2017, 10(4), 1011-1033. doi: 10.3934/krm.2017040 [11] Y. P. Choi and Z. Li, Emergent behavior of Cucker-Smale flocking particles with heterogeneous time delays, Appl. Math. Lett., 2018, 86, 49-56. doi: 10.1016/j.aml.2018.06.018 [12] F. Dalmao and E. Mordecki, Cucker-Smale flocking under hierarchical leadership and random interactions, SIAM J. Appl. Math., 2011, 71(4), 1307-1316. doi: 10.1137/100785910 [13] F. Dalmao and E. Mordecki, Hierarchical Cucker-Smale model subject to random failure, IEEE Trans. Autom. Control, 2012, 57(7), 1789-1793. doi: 10.1109/TAC.2012.2188440 [14] J. Dong, Flocking under hierarchical leadership with a free-will leader, Int. J. Robust Nonlinear Control, 2013, 23(16), 1891-1898. [15] R. Erban, J. Haskovec and Y. Sun, A Cucker-Smale model with noise and delay, SIAM J. Appl. Math., 2016, 76(4), 1535-1557. doi: 10.1137/15M1030467 [16] J. Haskovec, Flocking dynamics and mean-field limit in the Cucker-Smale-type model with topological interactions, Phys. D., 2013, 261, 42-51. doi: 10.1016/j.physd.2013.06.006 [17] S. Y. Ha and J. Liu, A simple proof of the Cucker-Smale flocking dynamics and mean field limit, Commun. Math. Sci., 2009, 7(2), 297-325. doi: 10.4310/CMS.2009.v7.n2.a2 [18] S. Y. Ha and E. Tadmor, From particle to kinetic and hydrodynamic description of flocking, Kinet. Relat. Models, 2008, 1(3), 415-435. doi: 10.3934/krm.2008.1.415 [19] S. Y. Ha and J. Liu, A simple proof of the Cucker-Smale flocking dynamics and mean-field limit, Commun. Math. Sci., 2009, 7(2), 297-325. doi: 10.4310/CMS.2009.v7.n2.a2 [20] S. Y. Ha, D. Ko and Y. Zhang, Critical coupling strength of the Cucker-Smale model for flocking, Math. Models Methods Appl. Sci., 2017, 27(6), 1051-1087. doi: 10.1142/S0218202517400097 [21] S. Y. Ha, J. Kim and X. Zhang, Uniform stability of the Cucker-Smale model and its application to the mean-field limit, Kinet. Relat. Models, 2018 11(5), 1157-1181. [22] M. W. Hirsch, S. Smale and R. Devaney, Differential Equations, Dynamical Systems, and an Introduction to Chaos, Academic Press, 2 edition, 2003. [23] C. Jin, Well posedness for pressureless Euler system with a flocking dissipation in Wasserstein space, Nonlinear Anal., 2015, 128, 412-422. doi: 10.1016/j.na.2015.08.003 [24] L. Li, D. W. C. Ho and S. Xu, A distributed event-triggered scheme for discretetime multi-agent consensus with communication delays, IET Control Theory Appl., 2014, 8(10), 830-837. doi: 10.1049/iet-cta.2013.0761 [25] L. Li, L. Huang and J. Wu, Cascade flocking with free-will, Discrete Contin. Dyn. Syst. Ser. B., 2016, 21(2), 497-522. [26] Z. Li, Effectual leadership in flocks with hierarchy and individual preference, Discrete Contin. Dyn. Syst., 2014, 34(9), 3683-3702. doi: 10.3934/dcds.2014.34.3683 [27] C. Li and S. Yang, A new discrete Cucker-Smale flocking model under hierarchical leadership, Discrete Contin. Dyn. Syst., Ser. B., 2016, 21(8), 2587-2599. doi: 10.3934/dcdsb.2016062 [28] Z. Li and X. Xue, Cucker-Smale flocking under rooted leadership with free-will agents, Physica A., 2014, 410, 205-217. doi: 10.1016/j.physa.2014.05.008 [29] Z. Li and X. Xue, Cucker-Smale flocking under rooted leadership with fixed and switching topologies, SIAM J. Appl. Math., 2010, 70(8), 3156-3174. doi: 10.1137/100791774 [30] Z. Li and S. Y. Ha, On the Cucker-Smale flocking with alternating leaders, Q. Appl. Math., 2015, 73(4), 693-709. doi: 10.1090/qam/1401 [31] Z. Li, S. Y. Ha and X. Xue, Emergent phenomena in an ensemble of Cucker-Smale particles underjoint rooted leadership, Math. Models Methods Appl. Sci., 2014, 24(7), 1389-1419. doi: 10.1142/S0218202514500043 [32] N. Mecholsky, E. Ott and T. M. Antonsen, Obstacle and predator avoidance in a model for flocking, Phys. D., 2010, 239(12), 988-996. doi: 10.1016/j.physd.2010.02.007 [33] S. Motsch and E. Tadmor, A new model for self-organized dynamics and its flocking behavior, J. Stat. Phys., 2011, 144(5), 923-947. doi: 10.1007/s10955-011-0285-9 [34] S. Motsch and E. Tadmor, Heterophilious dynamics enhances consensus, SIAM Rev., 2014, 56(4), 577-621. doi: 10.1137/120901866 [35] B. Piccoli, F. Rossi and E. Trelat, Control to flocking of the kinetic Cucker-Smale model, SIAM J. Math. Anal., 2015, 47(6), 4685-4719. doi: 10.1137/140996501 [36] J. Park, H. Kim and S. Y. Ha, Cucker-Smale flocking with inter-particle bonding forces, IEEE Trans. Automat. Control, 2010, 55(11), 2617-2623. doi: 10.1109/TAC.2010.2061070 [37] C. Pignotti and E. Trelat, Convergence to consensus of the general finitedimensional Cucker-Smale model with time-varying delays, Commun. Math. Sci., 2018, 16(8), 2053-2076. doi: 10.4310/CMS.2018.v16.n8.a1 [38] C. Pignotti and I. Reche Vallejo, Flocking estimates for the Cucker-Smale model with time lag and hierarchical leadership, J. Math. Anal. Appl., 2018, 464(2), 1313-1332. doi: 10.1016/j.jmaa.2018.04.070 [39] J. Qin and C. Yu, Cluster consensus control of generic linear multi-agent systems under directed topology with acyclic partition, Automatica, 2013, 49(9), 2898-2905. doi: 10.1016/j.automatica.2013.06.017 [40] L. Ru and X. Xue, Multi-cluster flocking behavior of the hierarchical Cucker-Smale model, J. Frankl. Inst., 2017, 354(5), 2371-2392. doi: 10.1016/j.jfranklin.2016.12.018 [41] L. Ru, Z. Li and X. Xue, Cucker-Smale flocking with randomly failed interactions, J. Frankl. Inst., 2015, 352(3), 1099-1118. doi: 10.1016/j.jfranklin.2014.12.007 [42] L. Ru and X. Xue, Flocking of Cucker-Smale model with intrinsic dynamics, Disc. Cont. Dyn. Syst. B., 2019, 24(12), 6817-6835. [43] J. Shen, Cucker-Smale flocking under hierarchical leadership, SIAM J. Appl. Math., 2007, 68(3), 694-719. [44] J. Toner and Y. Tu, Long-range order in a two-dimensional dynamical XY model: how birds fly together, Phys. Rev. Lett., 1995, 75, 4326-4329. doi: 10.1103/PhysRevLett.75.4326 -
-
Figures(4)
Export File
Citation
Chun-Bo Lian, Gang-Ling Hou, Bin Ge, Kang Zhou. MULTI-CLUSTER FLOCKING BEHAVIOR FOR A CLASS OF CUCKER-SMALE MODEL WITH A PERTURBATION[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1825-1851. doi: 10.11948/20200234
Format
Content
DownLoad:
- Figure 1. the flocking behaviors are common in nature
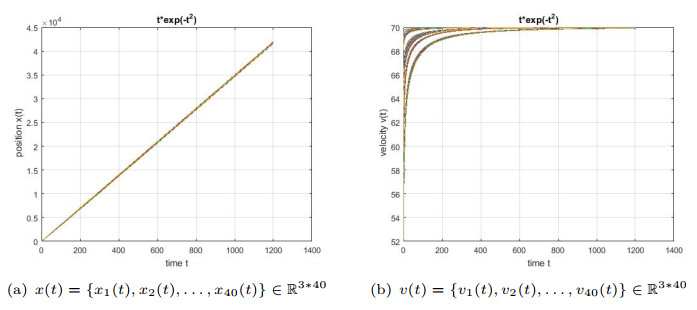
- Figure 2. Dynamic trends of velocity and position of 40 agents with disturbance systems
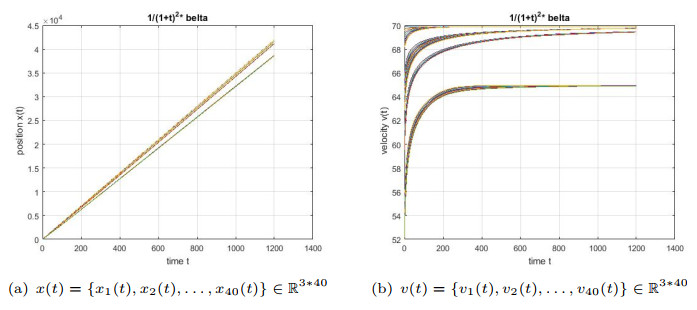
- Figure 3. Dynamic trends of velocity and position of 40 agents with disturbance systems
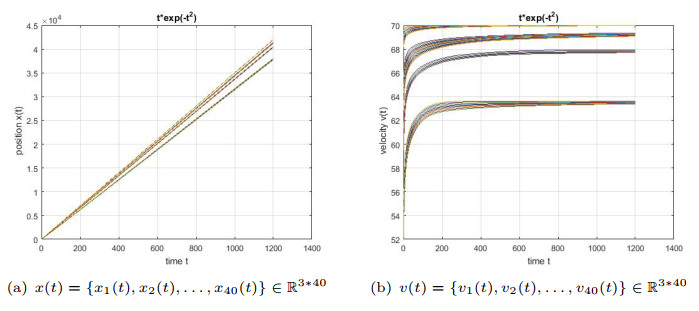
- Figure 4. Dynamic trends of velocity and position of 40 agents with disturbance systems