| Citation: | Lingshu Wang, Mei Zhang, Meizhi Jia. A DELAYED PREDATOR-PREY MODEL WITH PREY POPULATION GUIDED ANTI-PREDATOR BEHAVIOUR AND STAGE STRUCTURE[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1811-1824. doi: 10.11948/20200212 |
A DELAYED PREDATOR-PREY MODEL WITH PREY POPULATION GUIDED ANTI-PREDATOR BEHAVIOUR AND STAGE STRUCTURE
-
Abstract
We consider a predator-prey model with stage structure for the prey and anti-predator behaviour such that the adult prey can attack vulnerable predators. In which a time delay due to the gestation of the predator is incorporated into this model. By analyzing corresponding characteristic equations, the local stability of each of feasible equilibria and the existence of Hopf bifurcations at the positive equilibrium are established, respectively. By using Lyapunov functionals and LaSalleӳ invariance principle, sufficient conditions are obtained for the global stability of the trivial equilibrium, the predatorextinction equilibrium and the positive equilibrium, respectively. Numerical simulations are performed to illustrate the theoretical results.
-
Keywords:
- Predator-prey model /
- anti-predator behaviour /
- stage structure /
- time delay /
- Hopf bifurcation /
- stability
-

-
References
[1] W. G. Aiello and H. I. Freedman, A time delay model of single species growth with stage-structure, Math. Biosci., 1990, 101, 139-156. doi: 10.1016/0025-5564(90)90019-U [2] Y. Choh, M. Lgnacio, M. W. Sabelis and A. Janssen, Predator-prey role reversals, juvenile experience and adult antipredator behaviour, Scientific Reports, 2012, 2, 728. doi: 10.1038/srep00728 [3] S. Gourley and Y. Kuang, A stage structured predator-prey model and its dependence on maturation delay and death rate, J. Math. Biol., 2004, 49, 188-200. doi: 10.1007/s00285-004-0278-2 [4] J. Hale, Theory of Functional Differential Equation, Springer Heidelberg, 1977. [5] J. Huang, S. Ruan and J. Song, Bifurcations in a predator-prey system of Leslie type with generalized Holling type III functional response, J Diff. Equations, 2014, 257(6), 1721-1752. doi: 10.1016/j.jde.2014.04.024 [6] A. Janssen, F. Faraji, T. V. D. Hammen, S. Magalhaes and M. W. Sabelis, Interspecific infanticide deters predators, Ecology Letters, 2002, 5, 490-494. doi: 10.1046/j.1461-0248.2002.00349.x [7] Y. Kuang, Delay Differential Equation with Application in Population Synamics, Academic Press, New York, 1993. [8] S. L. Lima, Stress and decision-making under the risk of predation: recent developments from behavioral reproductive, and ecological perspectives, Advances in the Study of Behavior, 1998, 27, 215-290. [9] C. Liu, S. Li and Y. Yan, Hopf bifurcation analysis of a density predator-prey model with crowley-martin functional response and two time delays, Journal of Applied Analysis and Computation, 2019, 9(4), 1589-1605 doi: 10.11948/2156-907X.20190029 [10] S. G. Mortoja, P. Panja and S. K. Mondal, Dynamics of a predator-prey model with stage-structure on both species and anti-predator behavior, Informatics in Medicine Unlocked, 2018, 10, 50-57. doi: 10.1016/j.imu.2017.12.004 [11] A. Pallina, A. Jaassen and M. W. Sabelis, Predators induce interspecific herbivore competition for food in refuge space, Ecology Letters, 2010, 1, 171-177. [12] P. Panja and S. Mondal, Stability analysis of coexistence of three species prey-predator model, Nonlinear Dynam., 2015, 81, 373-82. doi: 10.1007/s11071-015-1997-1 [13] M. Perc and P. Grigolini, Collective behavior and evolutionary games -An introduction, Chaos, Solitons & Fractals, 2013, 56, 1-5. [14] R. A. Relvea, How prey response to combined predators: a review and an empirical test, Ecology, 2003, 84, 1827-1839. doi: 10.1890/0012-9658(2003)084[1827:HPRTCP]2.0.CO;2 [15] Y. Song, T. Yin and H. Shu, Dynamics of a ratio-dependent stage-structured predator-pery model with delay, Mathematical Methods in the Applied Sciences, 2017, 1-17. [16] X. Sun, Y. Li and Y. Xiao, A predator-prey model with prey population guided anti-predator behavior, International Journal of Bifurcation and Chaos, 2017, 27, 1750099-1-40. [17] X. Song and L. Chen, Optimal harvesting and stability for a two-species competetive system with stage structure, Math. Biosci., 2001, 170, 173-186. doi: 10.1016/S0025-5564(00)00068-7 [18] A. Szolnoki, M. Mobilia, L. Jiang, B. Szczesny, A. M. Rucklidge and M. Perc, Cyclic dominance in evolutionary games: a review, Journal of the Royal Society Interface, 2014, 11, 20140735. doi: 10.1098/rsif.2014.0735 [19] B. Tang and Y. Xiao, Bifurcation analysis of a predator-prey model with anti-predator behaviour, Chaos, Solitons & Fractals, 2015, 70, 58-68. [20] S. Wang, Research on the suitable living environment of the Rana temporaria chensinensis larva, Chinese, J. Zool., 1997, 31, 38-41. [21] C. Xu and Y. Yu, Stability analysis of time delay fraction order predator-prey system with crowley-martin functional response, Journal of Applied Analysis and Computation, 2019, 9(3), 928-942. doi: 10.11948/2156-907X.20180175 [22] R. Xu and Z. Ma, The effect of stage-structure on the permanence of a predator-prey system with time delay, Appl. Math. Comput., 2007, 189, 1164-1177. [23] R. Xu and Z. Ma, Stability and Hopf bifurcation in a predator-prey model with stage structure for the predator, Nonlinear Analysis: Real World Applications, 2008, 9(4), 1444-1460. doi: 10.1016/j.nonrwa.2007.03.015 [24] R. Yang and J. Ma, Analysis of a diffusive predator-prey system with anti-predator behaviour and maturation delay, Chaos, Solitons and Fractals, 2018, 109, 128-139. doi: 10.1016/j.chaos.2018.02.006 -
-
-
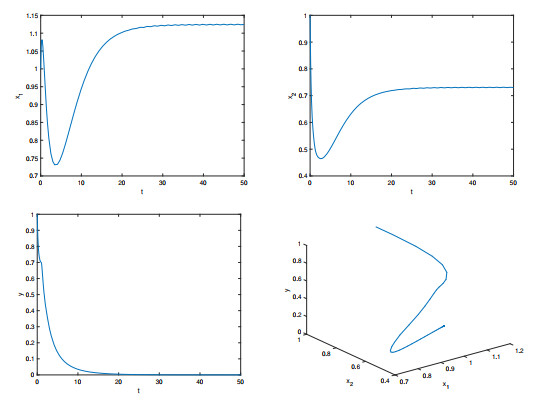
Figure 1. The temporal solution found by numerical integration of system (1.2) with
$ \tau = 0.5 $ and$ (\varphi_1(0), \varphi_2(0),\phi(0)) = (1, 1, 1) $ -
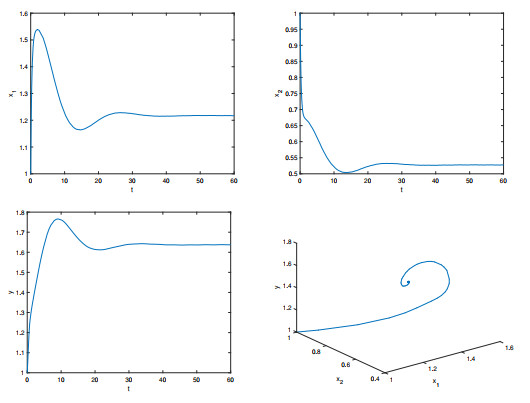
Figure 2. The temporal solution found by numerical integration of system (1.2) with
$ \tau = 0.5 $ and$ (\varphi_1(0), \varphi_2(0),\phi(0)) = (1, 1, 1) $ -
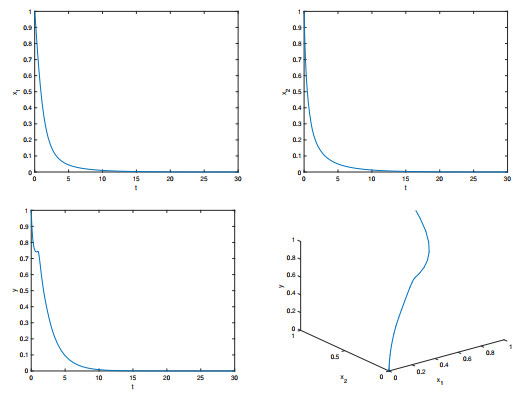
Figure 3. The temporal solution found by numerical integration of system (1.2) with
$ \tau = 0.5 $ and$ (\varphi_1(0), \varphi_2(0),\phi(0)) = (1, 1, 1) $ -
Figure 4. The temporal solution found by numerical integration of system (1.2) with
$ \tau = 15.706 $ and$ (\varphi_1(0), \varphi_2(0),\phi(0)) = (1, 1, 1) $




 DownLoad:
DownLoad: