| Citation: |
Jihua Yang. LIMIT CYCLE BIFURCATIONS IN A CLASS OF PIECEWISE SMOOTH DIFFERENTIAL SYSTEMS UNDER NON-SMOOTH PERTURBATIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2245-2257. doi: 10.11948/20200346
|
LIMIT CYCLE BIFURCATIONS IN A CLASS OF PIECEWISE SMOOTH DIFFERENTIAL SYSTEMS UNDER NON-SMOOTH PERTURBATIONS
-
Abstract
This paper deals with the problem of limit cycles of a class of piecewise smooth integrable differential systems with switching line $ x = 0 $. The generating functions of the associated first order Melnikov function satisfy two different Picard-Fuchs equations. By using the property of Chebyshev space, we obtain an upper bound for the number of limit cycles bifurcating from the period annulus under non-smooth perturbations of polynomials of degree $ n $. Finally, we present a concrete example to illustrate the theoretical result.
-
-
References
[1] A. Buicǎ and J. Llibre, Averaging methods for finding periodic orbits via Brouwer degree, Bull. Sci. Math., 2004, 128, 7-22. doi: 10.1016/j.bulsci.2003.09.002 [2] L. Gavrilov and I. Iliev, Quadratic perturbations of quadratic codimension-four centers, J. Math. Anal. Appl., 2009, 357, 69-76. doi: 10.1016/j.jmaa.2009.04.004 [3] M. Han, On the maximum number of periodic solutions of piecewise smooth periodic equations by average method, J. Appl. Anal. Comput., 2017, 7(2), 788-794. [4] M. Han and S. Liu, Further studies on limit cycle bifurcations for piecewise smooth near-Hamiltonian systems with multiple parameters, J. Appl. Anal. Comput., 2020, 10(2), 816-829. [5] M. Han, H. Sun and Z. Balanov. Upper estimates for the number of periodic solutions to multi-dimensional systems, J. Differential Equations, 2019, 266(12), 8281-8293. doi: 10.1016/j.jde.2018.12.034 [6] M. Han and L. Sheng, Bifurcation of limit cycles in piecewise smooth systems via Melnikov function, J. Appl. Anal. Comput., 2015, 5(4), 809-815. [7] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, J. Nonlinear Modeling and Analysis, 2021, 3(1), 13-34. [8] N. Hu and Z. Du, Bifurcation of periodic orbits emanated from a vertex in discontinuous planar systems, Commun. Nonlinear Sci. Numer. Simulat., 2013, 18(12), 3436-3448. doi: 10.1016/j.cnsns.2013.05.012 [9] E. Horozov and I. Iliev, Linear estimate for the number of zeros of Abelian integrals with cubic Hamiltonians, Nonlinearity, 1998, 11(6), 1521-1537. doi: 10.1088/0951-7715/11/6/006 [10] F. Liang, M. Han and V. Romanovski, Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian system with a homoclinic loop, Nonlinear Anal., 2012, 75, 4355-4374. doi: 10.1016/j.na.2012.03.022 [11] J. Llibre, A. Mereu and D. Novaes, Averaging theory for discontinuous piecewise differential systems, J. Differential Equations, 2015, 258(11), 4007-4032. doi: 10.1016/j.jde.2015.01.022 [12] F. Liang and M. Han, Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth systems, Chaos Solitons Fractals, 2012, 45(4) 454-464. doi: 10.1016/j.chaos.2011.09.013 [13] X. Liu and M. Han, Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems, Internat. J. Bifur. Chaos Appl. Sci. Engrg, 2010, 20(5), 1379-1390. doi: 10.1142/S021812741002654X [14] O. Ramirez and A. Alves, Bifurcation of limit cycles by perturbing piecewise non-Hamiltonian systems with nonlinear switching manifold, Nonlinear Analysis: Real World Applications, 2021, 57, 103188. doi: 10.1016/j.nonrwa.2020.103188 [15] J. Shi, W. Wang and X. Zhang, Limit cycles of polynomial Liénard systems via the averaging method, Nonlinear Analysis: Real World Applications, 2019, 45, 650-667. doi: 10.1016/j.nonrwa.2018.07.030 [16] S. Sui, J. Yang and L. Zhao, On the number of limit cycles for generic Lotka-Volterra system and Bogdanov-Takens system under perturbations of piecewise smooth polynomials, Nonlinear Analysis: Real World Applications, 2019, 49, 137-158. doi: 10.1016/j.nonrwa.2019.03.001 [17] Y. Wang, M. Han and D. Constantinescu, On the limit cycles of perturbed discontinuous planar systems with 4 switching lines, Chaos Solitons Fractals, 2016, 83(1), 158-177. [18] Y. Xiong and M. Han, Limit cycle bifurcations in discontinuous planar systems with multiple lines, J. Appl. Anal. Comput., 2020, 10(1), 361-377. [19] Y. Xiong and J. Hu, A class of reversible quadratic systems with piecewise polynomial perturbations, Applied Mathematics and Computation, 2019, 362(1), 124527. [20] J. Yang, Picard-Fuchs equation applied to quadratic isochronous systems with two switching lines, Internat. J. Bifur. Chaos, 2020, 30 (3), 2050042. doi: 10.1142/S021812742050042X [21] J. Yang and L. Zhao, Bounding the number of limit cycles of discontinuous differential systems by using Picard-Fuchs equations, J. Differential Equations, 2018, 264(9), 5734-5757. doi: 10.1016/j.jde.2018.01.017 [22] Y. Zhao and Z. Zhang, Linear estimate of the number of zeros of Abelian integrals for a kind of quartic Hamiltonians, J. Differential Equations, 1999, 155(1), 73-88. doi: 10.1006/jdeq.1998.3581 -
-
Figures(2)
Export File
Citation
Jihua Yang. LIMIT CYCLE BIFURCATIONS IN A CLASS OF PIECEWISE SMOOTH DIFFERENTIAL SYSTEMS UNDER NON-SMOOTH PERTURBATIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2245-2257. doi: 10.11948/20200346
Format
Content
DownLoad:
-
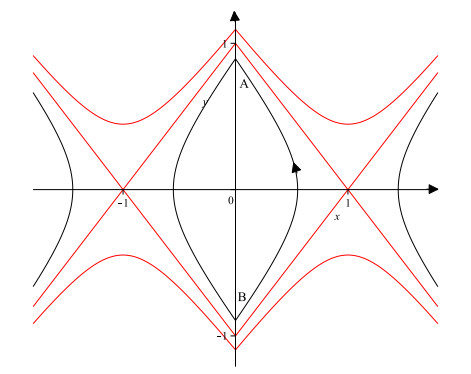
Figure 1. The closed orbits of system (1.1)
$ |_{\varepsilon = 0}. $ -
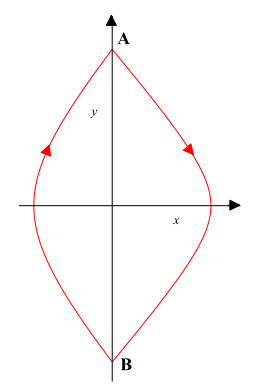
Figure 2. The closed orbits of system (3.1)
$ |_{\varepsilon = 0}. $