| Citation: |
Guang-hua Gao, Peng Xu, Rui Tang. FAST COMPACT DIFFERENCE SCHEME FOR THE FOURTH-ORDER TIME MULTI-TERM FRACTIONAL SUB-DIFFUSION EQUATIONS WITH THE FIRST DIRICHLET BOUNDARY[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2736-2761. doi: 10.11948/20200405
|
FAST COMPACT DIFFERENCE SCHEME FOR THE FOURTH-ORDER TIME MULTI-TERM FRACTIONAL SUB-DIFFUSION EQUATIONS WITH THE FIRST DIRICHLET BOUNDARY
-
Abstract
In this paper, a fast compact difference scheme is proposed for the initial-boundary value problem of fourth-order time multi-term fractional sub-diffusion equations with the first Dirichlet boundary conditions. Using the method of order reduction, the original problem can be converted to an equivalent lower-order system. Then at some super-convergence points, the multi-term Caputo derivatives are fast evaluated based on the sum-of-exponentials (SOE) approximation for the kernel functions appeared in Caputo fractional derivatives. The difficulty caused by the first Dirichlet boundary conditions is carefully handled. The energy method is used to illustrate the unconditional stability and convergence of the proposed fast compact scheme. The convergence accuracy is second-order in time and fourth-order in space if the solution has enough regularity. Compared with the direct scheme without the acceleration in time direction, the CPU time of the current fast scheme is largely reduced, which is shown by numerical examples.
-
-
References
[1] E. A. Abdel-Rehim, A. M. A. El-Sayed and A. S. Hashen, Simulation of the approximate solutions of the time-fractional multi-term wave equations, Comput. Math. Appl., 2017, 73, 1134-1154. doi: 10.1016/j.camwa.2016.06.019 [2] A. A. Alikhanov, A new difference scheme for the time fractional diffusion equation, J. Comput. Phys., 2015, 280, 424-438. doi: 10.1016/j.jcp.2014.09.031 [3] M. Amin, M. Abbas, M. K. lqbal and D. Baleanu, Non-polynomial quintic spline for numerical solution of fourth-order time fractional partial differential equations, Adv. Differ. Equ., 2019, 183. https://doi.org/10.1186/s13662-019-2125-1. doi: 10.1186/s13662-019-2125-1 [4] M. Cui, Compact difference scheme for time-fractional fourth-order equation with first Dirichlet boundary condition, East Asian J. Appl. Math., 2019, 9, 45-66. doi: 10.4208/eajam.260318.220618 [5] M. Fei and C. Huang, Galerkin-Legendre spectral method for the distributed-order time fractional fourth-order partial differential equation, Int. J. Comput. Math., 2020, 97, 1183-1196. doi: 10.1080/00207160.2019.1608968 [6] G. Gao, A. A. Alikhanov and Z. Sun, The temporal second order difference schemes based on the interpolation approximation for solving the time multi-term and distributed-order fractional sub-diffusion equations, J. Sci. Comput., 2017, 73, 93-121. doi: 10.1007/s10915-017-0407-x [7] G. Gao and R. Liu, A compact difference scheme for fourth-order temporal multi-term fractional wave equations and maximum error estimates, East Asian J. Appl. Math., 2019, 9, 703-722. doi: 10.4208/eajam.171118.060119 [8] G. Gao, R. Tang and Y. Qian, A compact finite difference scheme for the fourth-order time multi-term fractional sub-diffusion equations with the first Dirichlet boundary conditions, Int. J. Numer. Anal. Model., 2021, 18, 100-119. [9] G. Gao and Q. Yang, Fast evaluation of linear combinations of Caputo fractional derivatives and its appications to multi-term time-fractional sub-diffusion equations, Numer. Math. Theor. Meth. Appl., 2020, 13, 433-451. doi: 10.4208/nmtma.OA-2019-0013 [10] A. Gokdogan, A. Yildirim and M. Merdan, Solving a fractional order model of HIV infection of CD4(+) T cells, Math. Comput. Model., 2011, 54, 2132-2138. doi: 10.1016/j.mcm.2011.05.022 [11] X. Gu, H. Sun, Y. Zhang and Y. Zhao, Fast implicit difference schemes for time-space fractional diffusion equations with the integral fractional Laplacian, Math. Methods Appl. Sci., 2021, 44(1), 441-463. doi: 10.1002/mma.6746 [12] X. Hu and L. Zhang, A new implicit compact difference scheme for the fourth-order fractional diffusion-wave system, Int. J. Comput. Math., 2014, 91, 2215-2231. doi: 10.1080/00207160.2013.871000 [13] C. Huang and M. Stynes, Superconvergence of a finite element method for the multi-term time-fractional diffusion problem, J. Sci. Comput., 2020, 82(10), 10. https://doi.org/10.1007/s10915-019-01115-w. doi: 10.1007/s10915-019-01115-w [14] H. Jafari, M. Dehghan and K. Sayevand, Solving a fourth-order fractional diffusion-wave equation in a bounded domain by decomposition method, Numer. Methods Partial Differential Equ., 2008, 24, 1115-1126. doi: 10.1002/num.20308 [15] C. Ji, Z. Sun and Z. Hao, Numerical algorithms with high spatial accuracy for the fourth order fractional sub-diffusion equations with the first Dirichlet boundary conditions, J. Sci. Comput., 2016, 66, 1148-1174. doi: 10.1007/s10915-015-0059-7 [16] S. Jiang, J. Zhang, Q. Zhang and Z. Zhang, Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations, Commun. Comput. Phys., 2017, 21, 650-678. doi: 10.4208/cicp.OA-2016-0136 [17] B. Jin, R. Lazarov, Y. Liu and Z. Zhou, The Galerkin finite element method for a multi-term time-fractional diffusion equation, J. Comput. Phys., 2015, 281, 825-843. doi: 10.1016/j.jcp.2014.10.051 [18] H. Liao, Y. Yan and J. Zhang, Unconditional convergence of a fast two-level linearized algorithm for semilinear subdiffusion equations, J. Sci. Comput., 2019, 80, 1-25. doi: 10.1007/s10915-019-00927-0 [19] F. Liu, V. Anh and I. Turner, Numerical solution of the space fractional Fokker-Planck equation, Int. J. Comput. Appl. Math., 2004, 166, 209-219. [20] F. Liu, M. M. Meerschaert, R. J. McGough, P. Zhuang and Q. Liu, Numerical methods for solving the multi-term time-fractional wave-diffusion equation, Fract. Calc. Appl. Anal., 2013, 16, 9-25. doi: 10.2478/s13540-013-0002-2 [21] Y. Luchko, Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation, J. Math. Anal. Appl., 2011, 374, 538-548. doi: 10.1016/j.jmaa.2010.08.048 [22] P. Lyu, Y. Liang and Z. Wang, A fast linearized finite difference method for the nonlinear multi-term time-fractional wave equation, Appl. Numer. Math., 2020, 151, 448-471. doi: 10.1016/j.apnum.2019.11.012 [23] S. Nandal and D. N. Pandey, Numerical solution of non-linear fourth order fractional sub-diffusion wave equation with time delay, Appl. Math. Comput., 2020, 369, 124900. https://doi.org/10.1016/j.amc.2019.124900. doi: 10.1016/j.amc.2019.124900 [24] S. Nandal and D. N. Pandey, Numerical solution of time fractional non-linear neutral delay differential equations of fourth-order, Malaya Journal of Matematik, 2019, 7, 579-589. doi: 10.26637/MJM0703/0035 [25] S. Nandal and D. N. Pandey, Numerical treatment of non-linear fourth-order distributed fractional sub-diffusion equation with time-delay, Commun. Nonlinear Sci. Numer. Simulat., 2020, 83, 105146. doi: 10.1016/j.cnsns.2019.105146 [26] S. Nandal and D. N. Pandey, Second order compact difference scheme for time fractional sub-diffusion fourth-order neutral delay differential equations, Differ. Equ. Dyn. Syst., 2021, 29(1), 69-86. doi: 10.1007/s12591-020-00527-7 [27] S. C. Shiralashetti and A. B. Deshi, An efficient Harr wavelet collocation method for the numerical solution of multi-term fractional differential equations, Nonlinear Dyn., 2016, 83, 293-303. doi: 10.1007/s11071-015-2326-4 [28] S. S. Siddiqi and S. Arshed, Numerical solution of time-fractional fourth-order partial differential equations, Int. J. Comput. Math., 2015, 92, 1496-1518. doi: 10.1080/00207160.2014.948430 [29] V. Srivastava and K. N. Rai, A multi-term fractional diffusion equation for oxygen delivery through a capillary to tissues, Math. Comput. Model., 2010, 51, 616-624. doi: 10.1016/j.mcm.2009.11.002 [30] H. Sun and Z. Sun, A fast temporal second-order compact ADI difference scheme for the 2D multi-term fractional wave equation, Numer. Algor., 2020. https://doi.org/10.1007/s11075-020-00910-z. doi: 10.1007/s11075-020-00910-z [31] H. Sun, X. Zhao and Z. Sun, The temporal second order difference schemes based on the interpolation approximation for time multi-term fractional wave equation, J. Sci. Comput., 2019, 78, 467-498. doi: 10.1007/s10915-018-0820-9 [32] V. V. Uchaikin, On the fractional derivative model of the transport of cosmic rays in the Galaxy, JETP Lett., 2010, 91, 105-109. doi: 10.1134/S002136401003001X [33] S. Vong and Z. Wang, Compact finite difference scheme for the fourth-order fractional subdiffusion system, Adv. Appl. Math. Mech., 2014, 6, 419-435. doi: 10.4208/aamm.2014.4.s1 [34] L. Wei, Stability and convergence of a fully discrete local discontinuous Galerkin method for multi-term time fractional diffusion equations, Numer. Algor., 2017, 76, 695-707. doi: 10.1007/s11075-017-0277-1 [35] F. Xu, Y. Lai and X. Shu, Chaos in integer order and fractional order financial systems and their synchronization, Chaos Solitons Fractals, 2018, 117, 125-136. doi: 10.1016/j.chaos.2018.10.005 [36] D. Xu, W. Qiu and J. Guo, A compact finite difference scheme for the fourth-order time-fractional integro-differential equation with a weakly singular kernel, Numer. Methods Partial Differential Equations, 2020, 36, 439-458. doi: 10.1002/num.22436 [37] Y. Yan, Z. Sun and J. Jiang, Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: A second-order scheme, Commun. Comput. Phys., 2017, 22, 1028-1048. doi: 10.4208/cicp.OA-2017-0019 [38] Z. Yao and Z. Wang, A compact difference scheme for fourth-order fractional sub-diffusion equations with Neumann boundary conditions, J. Appl. Anal. Comput., 2018, 8, 1159-1169. [39] J. Zhang, F. Liu, Z. Lin and V. Anh, Analytical and numerical solutions of a multi-term time-fractional Burgers' fluid model, Appl. Math. Comput., 2019, 356, 1-12. -
-
Figures(2) / Tables(5)
Export File
Citation
Guang-hua Gao, Peng Xu, Rui Tang. FAST COMPACT DIFFERENCE SCHEME FOR THE FOURTH-ORDER TIME MULTI-TERM FRACTIONAL SUB-DIFFUSION EQUATIONS WITH THE FIRST DIRICHLET BOUNDARY[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2736-2761. doi: 10.11948/20200405
Format
Content
DownLoad:
-
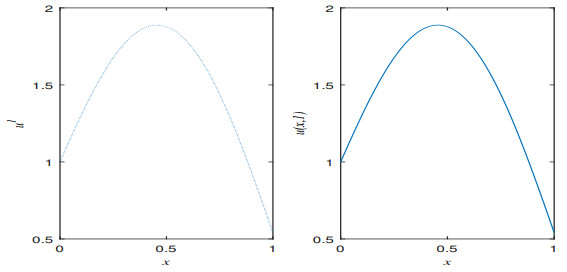
Figure 1. Numerical solution and exact solution plots for Example 5.1 with
$ t = 1 $ ,$ M = 100 $ ,$ N = 160 $ ,$ (\alpha_{0}, \alpha_{1}, \alpha_{2}) = (1/3, 1/4, 1/5) $ ,$ (\lambda_{0}, \lambda_{1}, \lambda_{2}) = (1, 2, 3) $ (Left$ \rm : Numerical solution; $ Right$ \rm : Exact\ solution) $ -
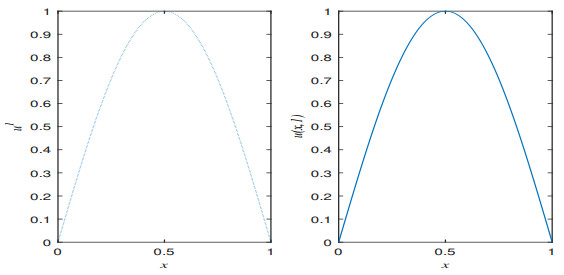
Figure 2. Numerical solution and exact solution plots for Example 5.2 with
$ t = 1 $ ,$ M = 100 $ ,$ N = 160 $ ,$ (\alpha_{0}, \alpha_{1}, \alpha_{2}) = (1/3, 1/4, 1/5) $ ,$ (\lambda_{0}, \lambda_{1}, \lambda_{2}) = (1, 2, 3) $ (Left$ \rm : Numerical solution; $ Right$ \rm : Exact\ solution) $