| Citation: |
Jian-Gen Liu, Xiao-Jun Yang, Yi-Ying Feng, Lu-Lu Geng. CHARACTERISTICS OF NEW TYPE ROGUE WAVES AND SOLITARY WAVES TO THE EXTENDED (3+1)-DIMENSIONAL JIMBO-MIWA EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2722-2735. doi: 10.11948/20200402
|
CHARACTERISTICS OF NEW TYPE ROGUE WAVES AND SOLITARY WAVES TO THE EXTENDED (3+1)-DIMENSIONAL JIMBO-MIWA EQUATION
-
Abstract
On the basis of the binary Bell polynomial scheme, the bilinear form of the extended (3+1)-dimensional Jimbo-Miwa (JM) equation, is constructed. Then, a class of new type rogue waves solutions to the extended (3+1)-dimensional JM equation, is found. It mainly includes the lump solutions, lumpoff solutions and instanton solutions. Their nonlinear evolutionary processes by 3D- and 2D-graphs, are shown. Finally, a direct method which is called the tanh-function method was used to get solitary waves of this considered model. These results can help us better understand interesting physical phenomena and mechanism.
-
Keywords:
- Extended (3+1)-dimensional JM equation /
- bilinear form /
- rogue waves /
- solitary waves
-
-
References
[1] K. K. Ali, R. I. Nuruddeen and A. R. Hadhoud, New exact solitary wave solutions for the extended (3+1)-dimensional Jimbo-Miwa equations, Result. Phys., 2018, 9(9), 12-16. [2] M. J. Ablowitz, M. A. Ablowitz and P. A. Clarkson, Solitons, nonlinear evolution equations and inverse scattering, Cambridge University Press, 1991. [3] E. Fan and K. W. Chow, Darboux covariant Lax pairs and infinite conservation laws of the (2+1)-dimensional breaking soliton equation, J. Math. Phys., 2011, 52(2), 023504. doi: 10.1063/1.3545804 [4] C. Gilson, F. Lambert, J. Nimmo and R. Willox, On the combinatorics of the Hirota D-operators, Proc. R. Soc. London, Ser. A., 1996, 452, 223. doi: 10.1098/rspa.1996.0013 [5] J. He, S. Xu and K. Porsezian, $ N$-order bright and dark rogue waves in a resonant erbium-doped fiber system. Phys. Rev. E., 2012, 86(6), 066603. doi: 10.1103/PhysRevE.86.066603 CrossRef $ N$-order bright and dark rogue waves in a resonant erbium-doped fiber system" target="_blank">Google Scholar
[6] R. Hirota, The direct method in soliton theory, Cambridge University Press, 2004. [7] F. Lambert, I. Loris and J. Springael, Classical Darboux transformations and the KP hierarchy, Inverse. Probl., 2001, 17, 1067. doi: 10.1088/0266-5611/17/4/333 [8] F. Lambert and J. Springael, Soliton equations and simple combinatorics, Acta Appl. Math., 2008, 102, 147. doi: 10.1007/s10440-008-9209-3 [9] X. Lü, B. Tian and K. Sun, et al, Bell-polynomial manipulations on the Bäcklund transformations and Lax pairs for some soliton equations with one Tau-function, J. Math. Phys., 2010, 51(11), 113506. doi: 10.1063/1.3504168 [10] J. Liu, X. Yang and Y. Feng, On integrability of the extended (3+1)-dimensional Jimbo-Miwa equation, Math. Meth. Appl. Sci., 2020, 43(4), 1646-1659. doi: 10.1002/mma.5991 [11] J. Liu, X. Yang, Y. Feng and L. Geng, On integrability of the higher-dimensional time fractional KdV-type equation, J. Geom. Phys., 2021, 160, 104000. doi: 10.1016/j.geomphys.2020.104000 [12] J. Liu and Y. Zhang, Construction of lump soliton and mixed lump stripe solutions of (3+1)-dimensional soliton equation, Result. Phys., 2018, 10, 94-98. doi: 10.1016/j.rinp.2018.05.022 [13] S. Lou and J. Lin, Rogue Waves in Nonintegrable KdV-Type Systems, Chin. Phys. Lett., 2018, 35(5), 050202. doi: 10.1088/0256-307X/35/5/050202 [14] H. Li and Y. Li, Meromorphic exact solutions of two extended (3+1)-dimensional JimbošCMiwa equations, Appl. Math. Comput., 2018, 333, 369-375. [15] J. Liu, X. Yang and Y. Feng, Characteristic of the algebraic traveling wave solutions for two extended (2+1)-dimensional Kadomtsev Petviashvili equations, Moder. Phys. Lett. A., 2020, 35(7), 20500285. [16] J. Liu, Y. Feng and H. Zhang, Exploration of the algebraic traveling wave solutions of a higher order model, Eng. Comput., 2021, 38(2), 618-631. doi: 10.1108/EC-07-2019-0303 [17] J. Lenells, Traveling wave solutions of the Camassa-Holm equation, J. Diff. Equ., 2005, 217(2), 393-430. doi: 10.1016/j.jde.2004.09.007 [18] W. Ma, Bilinear equations and resonant solutions characterized by Bell polynomials, Rep. Math. Phys., 2013, 72(1), 41-56. doi: 10.1016/S0034-4877(14)60003-3 [19] W. Ma and Y. Zhou, Lump solutions to nonlinear partial differential equations via Hirota bilinear forms, J. Diff. Equ., 2018, 264(4), 2633-2659. doi: 10.1016/j.jde.2017.10.033 [20] J. Manafian, B. Mohammadi-Ivatloo and M. Abapour, Lump-type solutions and interaction phenomenon to the (2+1)-dimensional Breaking Soliton equation, Appl. Math. Comput., 2019, 356, 13-41. [21] J. Manafian and M. Lakestani, Lump-type solutions and interaction phenomenon to the bidirectional Sawada-Kotera equation, Pramana., 2019, 92(3), 1-13. [22] J. Manafian and M. Lakestani, $ N$-lump and interaction solutions of localized waves to the (2+1)-dimensional variable-coefficient Caudrey-Dodd-Gibbon-Kotera-Sawada equation, J. Geom. Phys., 2020, 150, 103598. doi: 10.1016/j.geomphys.2020.103598 CrossRef $ N$-lump and interaction solutions of localized waves to the (2+1)-dimensional variable-coefficient Caudrey-Dodd-Gibbon-Kotera-Sawada equation" target="_blank">Google Scholar
[23] J. Manafian, O. A. Ilhan, L. Avazpour and A. A. Alizadeh, $ N$-lump and interaction solutions of localized waves to the (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation arise from a model for an incompressible fluid, Math. Meth. Appl. Sci., 2020, 43(17), 9904-9927. doi: 10.1002/mma.6665 CrossRef $ N$-lump and interaction solutions of localized waves to the (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation arise from a model for an incompressible fluid" target="_blank">Google Scholar
[24] J. Manafian and M. Lakestani, Interaction among a lump, periodic waves, and kink solutions to the fractional generalized CBS-BK equation, Math. Meth. Appl. Sci., 2021, 44(1), 1052-1070. doi: 10.1002/mma.6811 [25] J. Manafian, S. A. Mohammed, A. A. Alizadeh, H. M. Baskonus and W. Gao, Investigating lump and its interaction for the third-order evolution equation arising propagation of long waves over shallow water, Eur. J. Mech-B/Flui., 2020, 84, 289-301. doi: 10.1016/j.euromechflu.2020.04.013 [26] P. Müller and C. A. Garrett, Osborne Rogue waves Oceanography, 2005, 18, 66-75. [27] J. Manafian, Novel solitary wave solutions for the (3+1)-dimensional extended Jimbo-Miwa equations, Comput. Math. Appl., 2018, 76(5), 1246-1260. doi: 10.1016/j.camwa.2018.06.018 [28] W. Ma and J. H. Lee, A transformed rational function method and exact solutions to the (3+1)-dimensional Jimbo-Miwa equation, Chaos, Solitons & Fractals., 2009, 42(3), 1356-1363. [29] M. Onorato, S. Residori and U. Bortolozzo, et al, Rogue waves and their generating mechanisms in different physical contexts, Phys. Rep., 2013, 528(2), 47-89. doi: 10.1016/j.physrep.2013.03.001 [30] M. Singh and R. K. Gupta, Bäcklund transformations, Lax system, conservation laws and multisoliton solutions for Jimbo-Miwa equation with Bell-polynomials, Commun. Nonl. Sci. Numer. Simul., 2016, 37, 362-373. doi: 10.1016/j.cnsns.2016.01.023 [31] D. R. Solli, C. Ropers, P. Koonath and B. Jalali, Optical rogue waves, Nature, 2007, 450, 1054-1057. doi: 10.1038/nature06402 [32] D. R. Solli, C. Ropers and P. Koonath, Active control of rogue waves for stimulated supercontinuum generation, Phys. Revi. Lett., 2008, 101(23), 233902. doi: 10.1103/PhysRevLett.101.233902 [33] H. Sun and A. Chen, Lump and lump-kink solutions of the (3+1)-dimensional Jimbo-Miwa and two extended Jimbo-Miwa equations, Appl. Math. Lett., 2017, 68, 55-61. doi: 10.1016/j.aml.2016.12.008 [34] A. M. Wazwaz, Multiple-soliton solutions for extended (3+1)-dimensional Jimbo-Miwa equations, Appl. Math. Lett., 2016, 64, 21-26. [35] A. M. Wazwaz, The tanh method for traveling wave solutions of nonlinear equations, Appl. Math. Comput., 2004, 154(3), 713-723. [36] A. M. Wazwaz, The tanh method: exact solutions of the sine-Gordon and the sinh-Gordon equations, Appl. Math. Comput., 2005, 167(2), 1196-1210. [37] Z. Yan, Financial rogue waves, Commun. Theo. Phys., 2010, 54(5), 947. doi: 10.1088/0253-6102/54/5/31 [38] X. Yang, F. Gao and H. M. Srivastava, Exact travelling wave solutions for the local fractional two-dimensional burgers-type equations, Comput. Math. Appl., 2017, 73, 203-210. doi: 10.1016/j.camwa.2016.11.012 [39] X. Yang, J. T. Machado and D. Baleanu, Exact traveling-wave solution for local fractional boussinesq equation in fractal domain, Fractals., 2017, 25, 1740006. doi: 10.1142/S0218348X17400060 [40] Y. Zhang and H. Tam, Discussion on integrable properties for higher-dimensional variable-coefficient nonlinear partial differential equations, J. Math. Phys., 2013, 54(1), 013516. doi: 10.1063/1.4788665 -
-
Figures(3)
Export File
Citation
Jian-Gen Liu, Xiao-Jun Yang, Yi-Ying Feng, Lu-Lu Geng. CHARACTERISTICS OF NEW TYPE ROGUE WAVES AND SOLITARY WAVES TO THE EXTENDED (3+1)-DIMENSIONAL JIMBO-MIWA EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2722-2735. doi: 10.11948/20200402
Format
Content
DownLoad:
-
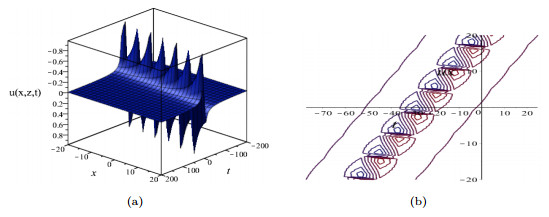
Figure 1. Plots of the lump solution
$ {u_{case_{2}}} $ with parameters$ {a_1} = 1, {k_2} = -2, {k_4} = 1 $ . (a) 3D-plot, with$ z = 20 $ . (b) 2D-contour plot. -
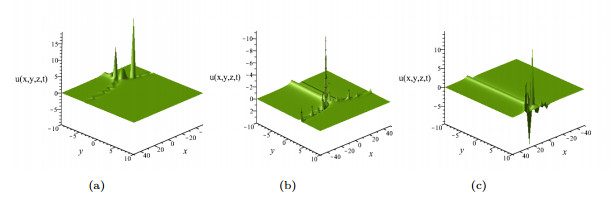
Figure 2. Plots of evolution of the lumpoff structures of solution
$ {u_{case_{5}}} $ with parameters$ {a_4} = 1, {k_2} = -2, {k_4} = 1, {k_5} = {a_5} = 0, b = -10, z = 2 $ . (a)$ t = -20 $ . (b)$ t = 0 $ . (c)$ t = 20 $ . -
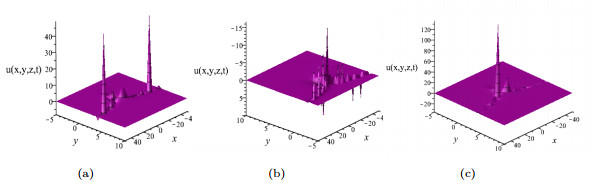
Figure 3. Plots of the instanton structures of solution
$ {u_{case_{15}}} $ with parameters$ {a_4} = 1, {k_2} = -2, {k_4} = 1, {k_5} = {a_5} = 0, b = -10, z = t = 0 $ . (a) 3D-plot,$ a = 2, b = -2 $ . (b) 3D-plot,$ a = -2, b = 2 $ .(c) 3D-plot,$ a = 2, b = -1 $ .