| Citation: | Yuan Zhou, Solomon Manukure. RATIONAL AND INTERACTIVE SOLUTIONS TO THE B-TYPE KADOMTSEV-PETVIASHVILI EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2473-2490. doi: 10.11948/20200446 |
RATIONAL AND INTERACTIVE SOLUTIONS TO THE B-TYPE KADOMTSEV-PETVIASHVILI EQUATION
-
Abstract
In this paper, a new method to find quadratic function solutions to bilinear forms is proposed. By applying the Hirota direct method, we construct some important exact solutions to the B-type Kadomtsev-Petviashvili (BKP) equation of fourth-order. Solitons, rational solutions, lump solutions and interaction solutions are presented with the help of symbolic computations. The dynamics of some selected solutions are also studied with the aid of 3D plots.
-
Keywords:
- Hirota method /
- the BKP equation /
- lump solutions /
- lump-kink solutions
-

-
References
[1] G. P. Agrawal, Nonlinear fiber optics, in Nonlinear Science at the Dawn of the 21st Century, Springer, 2000, 195-211. [2] I. S. Aranson, A. Pikovsky, N. F. Rulkov and L. S. Tsimring, Advances in Dynamics, Patterns, Cognition: Challenges in Complexity, 20, Springer, 2017. [3] H. Aref, Point vortex dynamics: a classical mathematics playground, J. Math. Phys., 2007, 48(6), 065401. doi: 10.1063/1.2425103 [4] H. Aref, Vortices and polynomials, Fluid Dyn. Res., 2007, 39(1-3), 5. doi: 10.1016/j.fluiddyn.2006.04.004 [5] H. Aref, P. K. Newton, M. A. Stremler et al., Vortex crystals, Adv. Appl. Mech., 2003, 39, 2-81. [6] I. Barashenkov and D. E. Pelinovsky, Exact vortex solutions of the complex sine-gordon theory on the plane, Phys. Lett. B, 1998, 436(1-2), 117-124. doi: 10.1016/S0370-2693(98)00841-7 [7] S. J. Chen, W. X. Ma and X. Lü, Bäcklund transformation, exact solutions and interaction behaviour of the (3+1)-dimensional Hirota-Satsuma-Ito-like equation, Commun. Nonlinear Sci. Numer. Simul., 2020, 83, 105135. doi: 10.1016/j.cnsns.2019.105135 [8] L. Cheng and Y. Zhang, Wronskian and linear superposition solutions to generalized KP and BKP equations, Nonlinear Dyn., 2017, 90(1), 355-362. doi: 10.1007/s11071-017-3666-z [9] P. A. Clarkson and E. Dowie, Rational solutions of the boussinesq equation and applications to rogue waves, Trans. Math. Its Appl., 2017, 1(1), tnx003. [10] E. Date, M. Jimbo, M. Kashiwara and T. Miwa, Transformation groups for soliton equations, in Proceedings of RIMS Symposium 1981 (Edited by M. Jimbo and T. Miwa), World Scientific Publishing Co., 1983, 39-120. [11] P. Deligne, P. I. Etingof and D. S. Freed, Quantum fields and strings: a course for mathematicians, 1, American Mathematical Society Providence, 1999. [12] P. G. Drazin and R. S. Johnson, Solitons: an introduction, Cambridge University Press, Cambridge, 1989. [13] S. Y. Eremenko, Atomic solitons as a new class of solitons, J. Nonlinear World, 2018, (6), 39-63. [14] A. S. Fokas and M. J. Ablowitz, On the inverse scattering transform of multidimensional nonlinear equations related to first-order systems in the plane, J. Math. Phys., 1984, 25(8), 2494-2505. doi: 10.1063/1.526471 [15] L. N. Gao, X. Y. Zhao, Y. Y. Zi et al., Resonant behavior of multiple wave solutions to a Hirota bilinear equation, Comput. Math. Appl., 2016, 72, 1225-1229. doi: 10.1016/j.camwa.2016.06.008 [16] L. N. Gao, Y. Y. Zi, Y. H. Yin et al., Bäcklund transformation, multiple wave solutions and lump solutions to a (3+1)-dimensional nonlinear evolution equation, Nonlinear Dyn., 2017, 89(3), 2233-2240. doi: 10.1007/s11071-017-3581-3 [17] C. R. Gilson and J. J. C. Nimmo, Lump solutions of the BKP equation, Phy. Lett. A, 1990, 147, 2705-2712. [18] R. Grimshaw, Korteweg de-vries equation, in Nonlinear waves in fluids: recent advances and modern applications, Springer, 2005, 1-28. [19] R. Hirota, Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons, Phys. Rev. Lett., 1971, 27, 1192-1194. doi: 10.1103/PhysRevLett.27.1192 [20] R. Hirota, Exact solution of the modified Korteweg-de Vries equation for multiple collisions of solitons, J. Phys. Soc. Japan, 1972, 33, 1456-1458. doi: 10.1143/JPSJ.33.1456 [21] R. Hirota, Exact solution of the sine-Gordon equation for multiple collisions of solitons, J. Phys. Soc. Japan, 1972, 33, 1459-1463. doi: 10.1143/JPSJ.33.1459 [22] R. Hirota, Soliton Solutions to the BKP Equations. I. the Pfaffian technique, J. Phys. Soc. Japan, 1989, 58, 2285-2296. doi: 10.1143/JPSJ.58.2285 [23] R. Hirota, Soliton Solutions to the BKP Equations. Ⅱ. The Integral Equation, J. Phys. Soc. Japan, 1989, 58, 2705-2712. doi: 10.1143/JPSJ.58.2705 [24] R. Hirota, The direct method in soliton theory, Cambridge University Press, Cambridge, 2004. [25] B. B. Kadomtsev and V. I. Petviashvili, On the stability of solitary waves in weakly dispersive media, Sov. Phys. Dokl., 1970, 15, 539-541. [26] Y. Kang, Y. Zhang and L. Jin, Soliton solution to BKP equation in Wronskian form, Appl. Math. Comput., 2013, 224, 250-258. [27] D. J. Kaup, The lump solutions and the Bäcklund transformation for the three-dimensional three-wave resonant interaction, J. Math. Phys., 1981, 22 (6), 1176-1181. doi: 10.1063/1.525042 [28] L. Kaur and A. M. Wazwaz, Bright-dark lump wave solutions for a new form of the (3+1)-dimensional bkp-boussinesq equation, Preprint. [29] L. Kaur and A. M. Wazwaz, Dynamical analysis of lump solutions for (3+1) dimensional generalized KP-Boussinesq equation and Its dimensionally reduced equations, Phys. Scr., 2018, 93(7), 075203. doi: 10.1088/1402-4896/aac8b8 [30] L. Kaur and A. M. Wazwaz, Bright-dark optical solitons for Schrödinger-Hirota equation with variable coefficients, Optik, 2019, 179, 479-484. doi: 10.1016/j.ijleo.2018.09.035 [31] L. Kaur and A. M. Wazwaz, Lump, breather and solitary wave solutions to new reduced form of the generalized BKP equation, Int. J. Num. Meth. Heat Fluid Flow, 2019, 29(2), 569-579. doi: 10.1108/HFF-07-2018-0405 [32] P. G. Kevrekidis, D. J. Frantzeskakis and R. Carretero-González, Emergent nonlinear phenomena in Bose-Einstein condensates: theory and experiment, 45, Springer Science & Business Media, 2007. [33] I. Kourakis and P. K. Shukla, Discrete breather modes associated with vertical dust grain oscillations in dusty plasma crystals, Phys. Plasmas, 2005, 12(1), 014502. doi: 10.1063/1.1824908 [34] Y. Liang, G. Wei and X. Li, Painlevé integrability, similarity reductions, new soliton and soliton-like similarity solutions for the (2+1)-dimensional BKP equation, Nonlinear Dyn., 2010, 62(1-2), 195-202. doi: 10.1007/s11071-010-9709-3 [35] X. Lü, New bilinear Bäcklund transformation with multisoliton solutions for the (2+1)-dimensional Sawada–Kotera model, Nonlinear Dyn., 2014, 76, 161-168. doi: 10.1007/s11071-013-1118-y [36] X. Lü and S. J. Chen, Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types, Nonlinear Dyn., 2021, 103, 947-977. doi: 10.1007/s11071-020-06068-6 [37] X. Lü, S. J. Chen and W. X. Ma, Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation, Nonlinear Dyn., 2016, 86, 523-534. doi: 10.1007/s11071-016-2905-z [38] X. Lü, S. T. Chen and W. X. Ma, Constructing lump solutions to a generalized Kadomtsev-Petviashvili-Boussinesq equation, Nonlinear Dyn., 2016, 86, 523-534. doi: 10.1007/s11071-016-2905-z [39] X. Lü, Y. F. Hua, S. J. Chen and X. F. Tang, Integrability characteristics of a novel (2+1)-dimensional nonlinear model: Painleve analysis, soliton solutions, Backlund transformation, Lax pair and infinitely many conservation laws, Commun. Nonlinear Sci. Numer. Simul., 2021, 95, 105612. doi: 10.1016/j.cnsns.2020.105612 [40] X. Lü and W. X. Ma, Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation, Nonlinear Dyn., 2016, 85, 1217-1222. doi: 10.1007/s11071-016-2755-8 [41] W. X. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Phys. Lett. A, 2015, 379, 1975-1978. doi: 10.1016/j.physleta.2015.06.061 [42] W. X. Ma and Y. Zhou, Lump solutions to nonlinear partial differential equations via Hirota bilinear forms, J. Diff. Eqs., 2018, 264, 2633-2659. doi: 10.1016/j.jde.2017.10.033 [43] W. X. Ma, Y. Zhou and R. Dougherty, Lump-type solutions to nonlinear differential equations derived from generalized bilinear equations, Int. J. Mod. Phys. B, 2016, 30, 1640018. doi: 10.1142/S021797921640018X [44] S. V. Manakov, V. E. Zakhorov, L. A. Bordag et al., Two-dimensional solitons of the Kadomtsev-Petviashvili equation and their interaction, Phys. Lett. A, 1977, 63, 205-206. doi: 10.1016/0375-9601(77)90875-1 [45] S. Manukure, A. Chowdhury and Y. Zhou, Complexiton solutions to the asymmetric Nizhnik-Novikov-Veselov equation, Int. J. Mod. Phys. B, 2019, 33, 1950098. doi: 10.1142/S021797921950098X [46] S. Manukure and Y. Zhou, A (2+1)-dimensional shallow water equation and its explicit lump solutions, Int. J. Mod. Phys. B, 2019, 33(7), 1950038. doi: 10.1142/S0217979219500383 [47] S. Manukure and Y. Zhou, A study of lump and line rogue wave solutions to a (2+1)-dimensional nonlinear equation, J. Geom. Phys., 2021, 167, 104274. doi: 10.1016/j.geomphys.2021.104274 [48] S. Manukure, Y. Zhou and W. X. Ma, Lump solutions to a (2+1)-dimensional extended KP equation, Comput. Math. Appl., 2018, 75(7), 2414-2419. doi: 10.1016/j.camwa.2017.12.030 [49] Y. Matsuno, Exact multi-soliton solution of the benjamin-ono equation, J. Phys. A Math. Gen, 1979, 12(4), 619. doi: 10.1088/0305-4470/12/4/019 [50] V. Matveev and M. Salle, Darboux transformations and solitons, Springer, Berlin, 1991. [51] J. McKenzie, The ion-acoustic soliton: A gas-dynamic viewpoint, Phys. Plasmas, 2002, 9(3), 800-805. doi: 10.1063/1.1445757 [52] J. J. C. Nimmo, Hall-littlewood symmetric functions and the BKP equation, J. Phys. A, 1990, 23(5), 751-760. doi: 10.1088/0305-4470/23/5/018 [53] J. J. C. Nimmo and A. Orlov, A relationship between rational and multi-soliton solutions of the BKP hierarchy, Glasgow Math. J., 2005, 47A, 149-168. [54] Y. Ogawa, Generalized q-functions and uc hierarchy of b-type, Tokyo J. Math., 2009, 32(2), 349-380. [55] N. Olver and I. V. Barashenkov, Complex sine-gordon-2: A new algorithm for multivortex solutions on the plane, Theor. Math. Phys., 2005, 144(2), 1223-1226. doi: 10.1007/s11232-005-0153-3 [56] D. E. Pelinovsky, Y. A. Stepanyants and Y. S. Kivshar, Self-focusing of plane dark solitons in nonlinear defocusing media, Phys. Rev. E, 1995, 51(5), 5016. doi: 10.1103/PhysRevE.51.5016 [57] M. Peyrard, Nonlinear dynamics and statistical physics of dna, Nonlinearity, 2004, 17(2), R1. doi: 10.1088/0951-7715/17/2/R01 [58] M. A. Porter, Experimental results related to dnls equations, in The Discrete Nonlinear Schrödinger Equation, Springer, 2009, 175-189. [59] H. O. Roshid and W. X. Ma, Dynamics of mixed lump-solitary waves of an extended (2+1)-dimensional shallow water wave model, Phys. Lett. A, 2018, 382(45), 3262-3268. doi: 10.1016/j.physleta.2018.09.019 [60] W. J. Rui and Y. F. Zhang, Soliton and lump-soliton solutions in the grammian form for the bogoyavlenskii-kadomtsev-petviashvili equation, Adv. Differ. Equ., 2020, 2020(1), 1-12. doi: 10.1186/s13662-019-2438-0 [61] J. Satsuma and M. J. Ablowitz, Two-dimensional lumps in nonlinear dispersive systems, J. Math. Phys., 1979, 20(7), 1496-1503. doi: 10.1063/1.524208 [62] J. Satsuma and Y. Ishimori, Periodic wave and rational soliton solutions of the benjamin-ono equation, J. Phys. Soc. Japan, 1979, 46(2), 681-687. doi: 10.1143/JPSJ.46.681 [63] A. Scott, Davydov's soliton, Phys. Rep., 1992, 217(1), 1-67. doi: 10.1016/0370-1573(92)90093-F [64] S. Singh, L. Kaur, K. Sakkaravarthi et al., Dynamics of higher-order bright and dark rogue waves in a new (2+1)-dimensional integrable boussinesq model, Phys. Scr., 2020, 95(11), 115213. doi: 10.1088/1402-4896/abbca0 [65] B. Sun and A. M. Wazwaz, Interaction of lumps and dark solitons in the Mel'nikov equation, Nonlinear Dyn., 2018, 92(2), 2049-2059. [66] H. Wang, Lump and interaction solutions to the (2+1)-dimensional Burgers equation, Appl. Math. Lett., 2018, 58, 27-34. [67] A. M. Wazwaz, Two B-type Kadomtsev-Petviashvili equations of (2+1) and (3+1) dimensions: multiple soliton solutions, rational solutions and periodic solutions, Comput. Fluids, 2013, 86, 357-362. doi: 10.1016/j.compfluid.2013.07.028 [68] A. M. Wazwaz, Painlevé analysis for a new integrable equation combining the modified Calogero-Bogoyavlenskii-Schiff (MCBS) equation with its negative-order form, Nonlinear Dyn., 2018, 92, 877-883. [69] A. M. Wazwaz and L. Kaur, Optical solitons for nonlinear Schrödinger (NLS) equation in normal dispersive regimes, Optik, 2019, 184, 428-435. doi: 10.1016/j.ijleo.2019.04.118 [70] G. B. Whitham, Linear and nonlinear waves, 42, John Wiley & Sons, 2011. [71] J. W. Xia, Y. W. Zhao and X. Lü, Predictability, fast calculation and simulation for the interaction solution to the cylindrical Kadomtsev-Petviashvili equation, Commun. Nonlinear Sci. Numer. Simul., 2020, 88, 105260. [72] H. N. Xu, W. Y. Ruan, Y. Zhang and X. Lü, Multi-exponential wave solutions to two extended Jimbo–Miwa equations and the resonance behavior, Appl. Math. Lett., 2020, 99, 105976. doi: 10.1016/j.aml.2019.07.007 [73] J. Y. Yang and W. X. Ma, Lump solutions of the BKP equation by symbolic computation, Int. J. Mod. Phys. B, 2016, 30, 1640028. doi: 10.1142/S0217979216400282 [74] J. Y. Yang, W. X. Ma and Z. Y. Qin, Abundant mixed lump-soliton solutions to the bkp equation, East Asian J. Appl. Math., 2018, 8(2), 224-232. doi: 10.4208/eajam.210917.051217a [75] Y. H. Yin, S. J. Chen and X. Lü, Study on localized characteristics of lump and interaction solutions to two extended Jimbo–Miwa equations, Chin. Phys. B, 2020, 29, 120502. doi: 10.1088/1674-1056/aba9c4 [76] Y. H. Yin, W. X. Ma, J. G. Liu and X. Lü, Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 2018, 76, 1275-1283. doi: 10.1016/j.camwa.2018.06.020 [77] J. B. Zhang and W. X. Ma, Mixed lump-kink solutions to the BKP equation, Comp. Math. Appl., 2017, 74, 591-596. doi: 10.1016/j.camwa.2017.05.010 [78] J. Zhao, J. Manafian, N. E. Zaya and S. A. Mohammed, Multiple rogue wave, lump-periodic, lump-soliton, and interaction between k-lump and k-stripe soliton solutions for the generalized kp equation, Math. Method. Appl. Sci., 2021, 44(6), 5079-5098. doi: 10.1002/mma.7093 [79] Y. Zhou and W. X. Ma, Applications of linear superposition principle to resonant solitons and complexitons, Comput. Math. Appl., 2017, 73, 1697-1706. doi: 10.1016/j.camwa.2017.02.015 [80] Y. Zhou and W. X. Ma, Complexiton solutions to nonlinear partial differential equations by the direct method, J. Math. Phys., 2017, 58, 101511. doi: 10.1063/1.4996358 [81] Y. Zhou and S. Manukure, Complexiton solutions to the Hirota-Satsuma-Ito equation, Math. Method Appl. Sci., 2019, 42, 1-8. doi: 10.1002/mma.5148 [82] Y. Zhou, S. Manukure and W. X. Ma, Lump and lump-soliton solutions to the Hirota-Satsuma-Ito equation, Commun. Nonlin. Sci. Numer. Simul., 2019, 68, 56-62. doi: 10.1016/j.cnsns.2018.07.038 [83] Y. Zhou, S. Manukure and M. McAnally, Lump and rogue wave solutions to a (2+1)-dimensional boussinesq type equation, J. Geom. Phys., 2021, 167, 104275. doi: 10.1016/j.geomphys.2021.104275 -
-
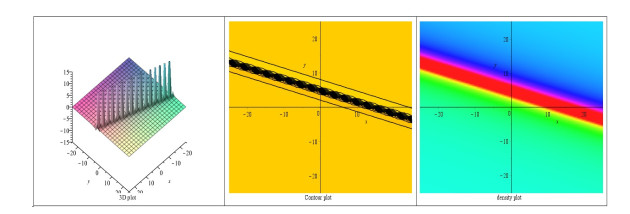
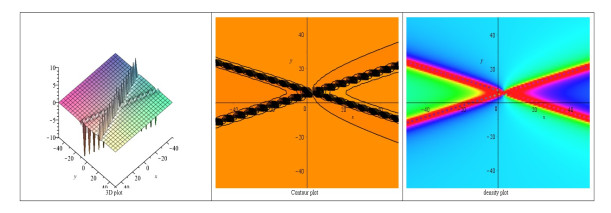
- Figure 1. A rational solution to the BKP equation
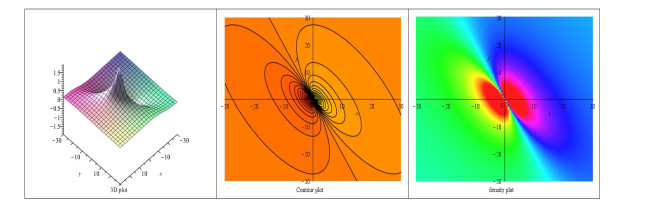
- Figure 2. Another rational solution to the BKP equation
- Figure 3. Lump solution to the BKP equation
-
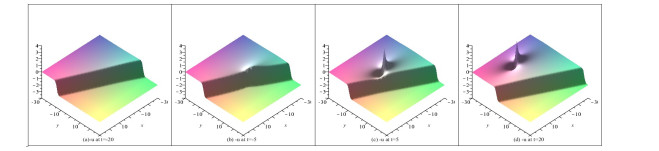
Figure 4. The graphs of the
$ -u $ when (a)$ t = -20 $ , (b)$ t = -5 $ , (c)$ t = 5 $ , (d)$ t = 20 $ . -
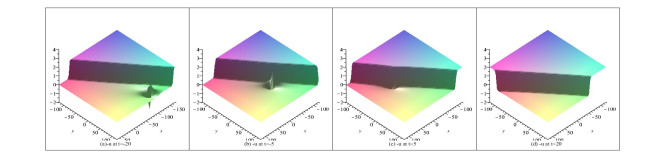
Figure 5. The graphs of the
$ -u $ when (a)$ t = -20 $ , (b)$ t = -5 $ , (c)$ t = 5 $ , (d)$ t = 20 $ .




 DownLoad:
DownLoad: