| Citation: |
Xijun Deng, Yusheng Jia, Mingji Zhang. STUDIES ON CURRENT-VOLTAGE RELATIONS VIA POISSON-NERNST-PLANCK SYSTEMS WITH MULTIPLE CATIONS AND PERMANENT CHARGES[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 932-951. doi: 10.11948/20210003
|
STUDIES ON CURRENT-VOLTAGE RELATIONS VIA POISSON-NERNST-PLANCK SYSTEMS WITH MULTIPLE CATIONS AND PERMANENT CHARGES
-
Abstract
We study a one-dimensional Poisson-Nernst-Planck system with multiple cations having the same valences and small permanent charges. Viewing the permanent charge as a small parameter, via regular perturbation analysis, approximations of the current-voltage (I-V) relations are derived explicitly, and this allows us to further study the qualitative properties of ionic flows through membrane channels. Our main interest are small permanent charge and channel geometry effects on the I-V relations, which additionally depend on the nonlinear interactions with other physical parameters involved in the model. Critical potentials are identified and their important roles played in the study of the property of ionic flows are characterized. We perform numerical simulations to provide more intuitive illustrations of our theoretical results. Those non-intuitive observations from analysis of the system provide better understandings of the mechanism of ionic flows through membrane channels, particularly the internal dynamics that is not able to be detected via current technology.
-
Keywords:
- PNP /
- diffusion coefficients /
- permanent charges /
- channel geometry /
- electroneutrality conditions
-
-
References
[1] B. Alberts, D. Bray, J. Lewis, M. Raff, K. Roberts and D. J. Watson, Molecular Biology of the Cell, 3rd ed., Garland, New York, 1994. [2] V. Barcilon, Ion flow through narrow membrane channels: Part I, SIAM J. Appl. Math., 1992, 52, 1391–1404. doi: 10.1137/0152080 [3] J. Barthel, H. Krienke and W. Kunz, Physical Chemistry of Electrolyte Solutions: Modern Aspects, Springer-Verlag, New York, 1998. [4] P. W. Bates, J. Chen and M. Zhang, Dynamics of ionic flows via Poisson-Nernst-Planck systems with local hard-sphere potentials: Competition between cations, Math. Biosci. Eng., 2020, 17, 3736–3766. doi: 10.3934/mbe.2020210 [5] P. W. Bates, Y. Jia, G. Lin, H. Lu and M. Zhang, Individual flux study via steady-state Poisson-Nernst-Planck systems: Effects from boundary conditions, SIAM J. on Appl. Dyn. Syst., 2017, 16, 410–430. doi: 10.1137/16M1071523 [6] P. W. Bates, Z. Wen and M. Zhang, Small permanent charge effects on individual fluxes via Poisson-Nernst-Planck models with multiple cations, J. Nonlinear Sci., 2021, 31, 1–62. doi: 10.1007/s00332-020-09667-0 [7] M. Bazant, K. Thornton and A. Ajdari, Diffuse-charge dynamics in electrochemical systems, Phys. Review E, 2004, 70, 1–24. [8] M. Z. Bazant, K. Chu and B. J. Bayly, Current-voltage relations for electrochemical thin films, SIAM J. Appl. Math., 2005, 65, 1463–1484. doi: 10.1137/040609938 [9] D. Chen and R. S. Eisenberg, Charges, currents and potentials in ionic channels of one conformation, Biophys. J., 1993, 64, 1405–1421. doi: 10.1016/S0006-3495(93)81507-8 [10] J. Chen, Y. Wang, L. Zhang and M. Zhang, Mathematical analysis of Poisson-Nernst-Planck models with permanent charges and boundary layers: Studies on individual fluxes, Nonlinearity, 2021, 34, 3879–3906. doi: 10.1088/1361-6544/abf33a [11] J. Chen and M. Zhang, Boundary layer effects on ionic flows via Poisson-Nernst-Planck systems with nonuniform ion sizes, Discrete Contin. Dyn. Syst., Series B, doi:10.3934/dcdsb.2021312. [12] B. Eisenberg, Proteins, Channels, and Crowded Ions, Biophys. Chem., 2003, 100, 507–517. [13] B. Eisenberg, Ions in Fluctuating Channels: Transistors Alive, Fluctuation and Noise Letters, 2012, 11, 76–96. [14] B. Eisenberg, Crowded charges in ion channels, In Advances in Chemical Physics; Rice, S. A. Ed., John Wiley & Sons: Hoboken, NJ, USA, 2011, 77–223. [15] R. S. Eisenberg, From Structure to Function in Open Ionic Channels, J. Memb. Biol., 1999, 71, 1–24. [16] B. Eisenberg and W. Liu, Poisson-Nernst-Planck systems for ion channels with permanent charges, SIAM J. Math. Anal., 2007, 38, 1932–1966. doi: 10.1137/060657480 [17] B. Eisenberg, W. Liu and H. Xu, Reversal charge and reversal potential: case studies via classical Poisson-Nernst-Planck models, Nonlinearity, 2015, 28, 103–128. doi: 10.1088/0951-7715/28/1/103 [18] D. Gillespie, A singular perturbation analysis of the Poisson-Nernst-Planck system: Applications to Ionic Channels, Ph. D Thesis, Rush University at Chicago, Chicago, IL, USA, 1999. [19] D. Gillespie and R. S. Eisenberg, Physical descriptions of experimental selectivity measurements in ion channels, European Biophys. J., 2002, 31, 454–466. doi: 10.1007/s00249-002-0239-x [20] D. Gillespie, W. Nonner and R. S. Eisenberg, Coupling Poisson-Nernst-Planck and density functional theory to calculate ion flux, J. Phys. Condens. Matter, 2002, 14, 12129–12145. doi: 10.1088/0953-8984/14/46/317 [21] L. J. Henderson, The Fitness of the Environment: an Inquiry Into the Biological Significance of the Properties of Matter, Macmillan, New York, 1927. [22] Y. Hyon, B. Eisenberg and C. Liu, A mathematical model for the hard sphere repulsion in ionic solutions, Commun. Math. Sci., 2010, 9, 459–475. [23] Y. Hyon, J. Fonseca, B. Eisenberg and C. Liu, A new Poisson-Nernst-Planck equation (PNP-FS-IF) for charge inversion near walls, Biophys. J., 2011, 100, 578a. [24] W. Im and B. Roux, Ion permeation and selectivity of OmpF porin: a theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory, J. Mol. Biol., 2002, 322, 851–869. doi: 10.1016/S0022-2836(02)00778-7 [25] S. Ji and W. Liu, Poisson-Nernst-Planck Systems for Ion Flow with Density Functional Theory for Hard-Sphere Potential: I-V relations and Critical Potentials. Part I: Analysis, J. Dyn. Diff. Equat., 2012, 24, 955–983. doi: 10.1007/s10884-012-9277-y [26] S. Ji and W. Liu, Flux ratios and channel structures, J. Dynam. Differ. Equations, 2019, 31, 1141–1183. doi: 10.1007/s10884-017-9607-1 [27] S. Ji, W. Liu and M. Zhang, Effects of (small) permanent charges and channel geometry on ionic flows via classical Poisson-Nernst-Planck models, SIAM J. on Appl. Math., 2015, 75, 114–135. doi: 10.1137/140992527 [28] C. Jones, Geometric singular perturbation theory, Dynamical systems (Montecatini Terme, 1994, 44–118. Lect. Notes in Math., 1609. Springer, Berlin, 1995. [29] G. Lin, W. Liu, Y. Yi and M. Zhang, Poisson-Nernst-Planck systems for ion flow with density functional theory for local hard-sphere potential, SIAM J. on Appl. Dyn. Syst., 2013, 12, 1613–1648. doi: 10.1137/120904056 [30] W. Liu, Geometric singular perturbation approach to steady-state Poisson-Nernst-Planck systems, SIAM J. Appl. Math., 2005, 65, 754–766. doi: 10.1137/S0036139903420931 [31] W. Liu, One-dimensional steady-state Poisson-Nernst-Planck systems for ion channels with multiple ion species, J. Differential Equations, 2009, 246, 428–451. doi: 10.1016/j.jde.2008.09.010 [32] W. Liu, A flux ratio and a universal property of permanent charges effects on fluxes, Comput. Math. Biophys., 2018, 6, 28–40. doi: 10.1515/cmb-2018-0003 [33] W. Liu and H. Xu, A complete analysis of a classical Poisson-Nernst-Planck model for ionic flow, J. Differential Equations, 2015, 258, 1192–1228. doi: 10.1016/j.jde.2014.10.015 [34] W. Nonner and R. S. Eisenberg, Ion permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-type Calcium channels, Biophys. J., 1998, 75, 1287–1305. doi: 10.1016/S0006-3495(98)74048-2 [35] S. Y. Noskov, S. Berneche and B. Roux, Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature, 2004, 431, 830–834. [36] S. Y. Noskov and B. Roux, Ion selectivity in potassium channels, Biophys. Chem., 2006, 124, 279–291. doi: 10.1016/j.bpc.2006.05.033 [37] J. K. Park and J. W. Jerome, Qualitative properties of steady-state Poisson-Nernst-Planck systems: Mathematical study, SIAM J. Appl. Math., 1997, 57, 609–630. doi: 10.1137/S0036139995279809 [38] B. Roux, T. W. Allen, S. Berneche and W. Im, Theoretical and computational models of biological ion channels, Quat. Rev. Biophys., 2004, 37, 15–103. doi: 10.1017/S0033583504003968 [39] D. J. Rouston, Bipolar Semiconductor Devices, McGraw-Hill, New York, 1990. [40] Z. Schuss, B. Nadler and R. S. Eisenberg, Derivation of Poisson and Nernst-Planck equations in a bath and channel from a molecular model, Phys. Rev. E, 2001, 64, 1–14. [41] B. G. Streetman, Solid State Electronic Devices, 4th ed., Prentice-Hall, Englewood Cliffs, NJ, 1972. [42] C. Tanford, Reynolds, J. Nature's Robots: A History of Proteins, Oxford University Press, New York, 2001. [43] Y. Wang, L. Zhang and M. Zhang, Studies on individual fluxes via Poisson-Nernst-Planck models with small permanent charges and partial electroneutrality conditions, J. Appl. Anal. Comput., doi: 10.11948/20210045. [44] J. R. M. Warner, Microelectronics: Its unusual origin and personality, IEEE Trans. Electron. Devices, 2001, 48, 2457–2467. doi: 10.1109/16.960368 [45] Z. Wen, P. W. Bates and M. Zhang, Effects on I-V relations from small permanent charge and channel geometry via classical Poisson-Nernst-Planck equations with multiple cations, Nonlinearity, 2021, 34, 4464–4502. doi: 10.1088/1361-6544/abfae8 [46] Z. Wen, L. Zhang and M. Zhang, Dynamics of classical Poisson-Nernst-Planck systems with multiple cations and boundary layers, J. Dyn. Diff. Equat., 2021, 33, 211–234. doi: 10.1007/s10884-020-09861-4 [47] L. Zhang, B. Eisenberg and W. Liu, An effect of large permanent charge: Decreasing flux with increasing transmembrane potential, Eur. Phys. J. Special Topics, 2019, 227, 2575–2601. doi: 10.1140/epjst/e2019-700134-7 [48] M. Zhang, Competition between cations via Poisson-Nernst-Planck systems with nonzero but small permanent charges, Membranes, 2021, 11, 236. doi: 10.3390/membranes11040236 -
-
Figures(7)
Export File
Citation
Xijun Deng, Yusheng Jia, Mingji Zhang. STUDIES ON CURRENT-VOLTAGE RELATIONS VIA POISSON-NERNST-PLANCK SYSTEMS WITH MULTIPLE CATIONS AND PERMANENT CHARGES[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 932-951. doi: 10.11948/20210003
Format
Content
DownLoad:
-
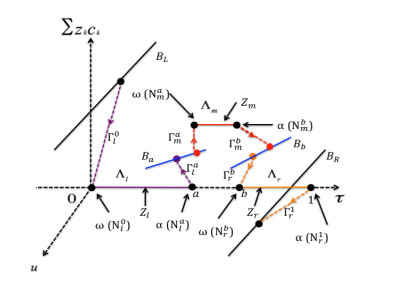
Figure 1. Illustration of a singular orbit projected to the space of
$ (u, \sum z_kc_k, \tau) $ under current setup. -
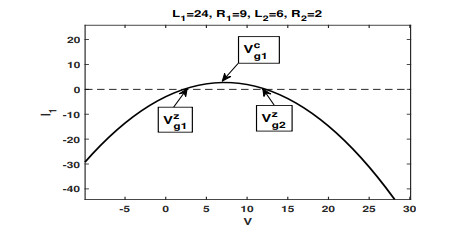
Figure 2.
$ {\cal I}_1(V;\varepsilon) $ , the approximation of$ {\cal I}_{1}(V) $ , has two zeros$ V_{g1}^z $ and$ V_{g2}^z $ , and a critical point$ V_{g1}^{c} $ with$ V_{g1}^z<V_{g1}^c<V_{g2}^z $ . -
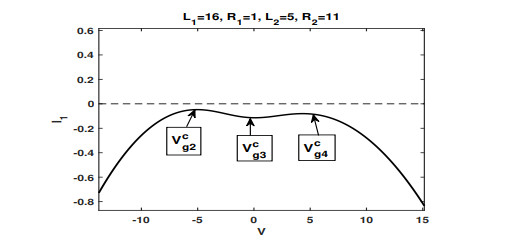
Figure 3.
$ {\cal I}_1(V;\varepsilon) $ , the approximation of$ {\cal I}_{1}(V) $ , has no zeros, but has three critical point$ V_{g2}^c, V_{g3}^c $ and$ V_{g4}^c $ with$ V_{g2}^c<V_{g3}^c<V_{g4}^c $ . -
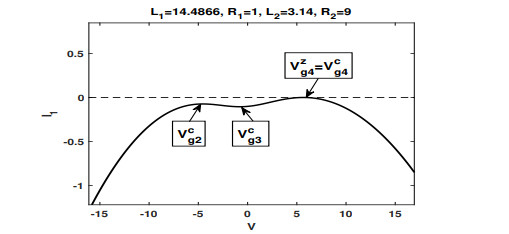
Figure 4.
$ {\cal I}_1(V;\varepsilon) $ , the approximation of$ {\cal I}_{1}(V) $ , has a unique zero$ V_{g4}^z $ , and three critical point$ V_{g2}^c, V_{g3}^c $ and$ V_{g4}^c $ with$ V_{g2}^c<V_{g3}^c<V_{g4}^c=V_{g4}^z $ . -
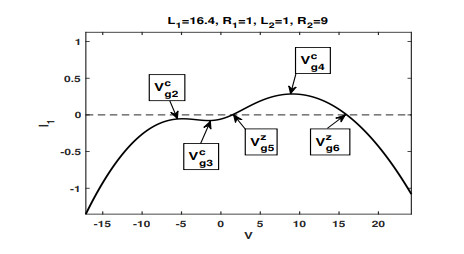
Figure 5.
$ {\cal I}_1(V;\varepsilon) $ , the approximation of$ {\cal I}_{1}(V) $ , has two zeros$ V_{g5}^z $ and$ V_{g6}^z $ and three critical point$ V_{g2}^c, V_{g3}^c $ and$ V_{g4}^c $ with$ V_{g2}^c<V_{g3}^c<V_{g5}^z<V_{g4}^c<V_{g6}^z $ . -
Figure 6.
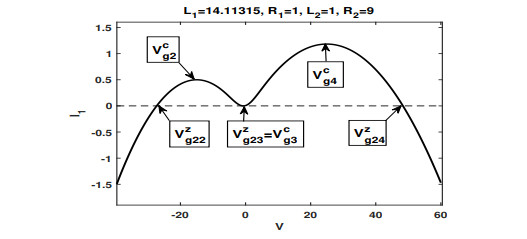
$ {\cal I}_1(V;\varepsilon) $ , the approximation of$ {\cal I}_{1}(V) $ , has three zeros$ V_{g22}^z, \ V_{g23}^z, \ V_{g24}^z $ , and three critical point$ V_{g2}^c, V_{g3}^c $ and$ V_{g4}^c $ with$ V_{g22}^z<V_{g2}^c<V_{g3}^c=V_{g23}^z<V_{g4}^c<V_{g24}^z $ . -
Figure 7.
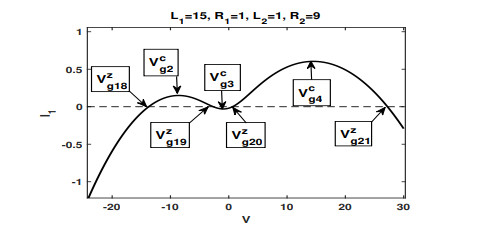
$ {\cal I}_1(V;\varepsilon) $ , the approximation of$ {\cal I}_{1}(V) $ , has four zeros$ V_{g18}^z, \ V_{g19}^z, \ V_{g20}^z, \ V_{g21}^z $ and three critical point$ V_{g2}^c, V_{g3}^c $ and$ V_{g4}^c $ with$ V_{g18}^z<V_{g2}^c<V_{g19}^z<V_{g3}^c<V_{g20}^z<V_{g4}^c<V_{g21}^z $ .