| Citation: |
Haicheng Liu, Bin Ge, Qiyuan Liang, Jiaqi Chen. A DELAYED SEMILINEAR PARABOLIC PREDATOR-PREY SYSTEM WITH HABITAT COMPLEXITY AND HARVESTING EFFECTS[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2561-2582. doi: 10.11948/20210015
|
A DELAYED SEMILINEAR PARABOLIC PREDATOR-PREY SYSTEM WITH HABITAT COMPLEXITY AND HARVESTING EFFECTS
-
Abstract
In this paper, we propose a delayed reaction-diffusive system with habitat complexity and harvesting effects, and study dynamic behaviors of the system. Firstly, for the system without time delay, the stability of equilibria is studied. It is found that when habitat complexity reaches a certain critical value, the positive equilibrium will change from unstable to locally asymptotically stable. Secondly, time delay effect on the dynamic behaviors of diffusion system is studied. The existence conditions of Hopf bifurcation are given, and the properties of bifurcating periodic solutions are studied by using the center manifold and normal form theories, including the direction of Hopf bifurcation, the stability of bifurcating periodic solutions and the period. Finally, the corresponding numerical simulations and biological interpretation are made to verify the results of theoretical analysis.
-
Keywords:
- Predator-prey system /
- habitat complexity effect /
- harvesting effect /
- time delay /
- diffusion term
-
-
References
[1] M. Agarwal and R. Pathak, Harvesting and Hopf Bifurcation in a prey-predator model with Holling Type IV Functional Response, International Journal of Mathematics & Soft Computing, 2012, 2(1), 83-92. [2] A. A. Berryman and A. Alan, The origins and evolution of predator-prey theory, Ecology, 1992, 73(5), 1530-1535. doi: 10.2307/1940005 [3] N. Bairagi and D. Jana, On the stability and Hopf bifurcation of a delay-induced predator-prey system with habitat complexity, Applied Mathematical Modelling, 2011, 35(7), 3255-3267. doi: 10.1016/j.apm.2011.01.025 [4] K. Belkhodja, A. Moussaoui and M. Alaoui, Optimal harvesting and stability for a prey-predator model, Nonlinear Analysis: Real World Applications, 2018, 39, 321-336. doi: 10.1016/j.nonrwa.2017.07.004 [5] C. Çelik, The stability and Hopf bifurcation for a predator-prey system with time delay, Chaos Solitons & Fractals, 2008, 37(1), 87-99. [6] J. B. Collings, The effects of the functional response on the bifurcation behavior of a mite predator-prey interaction model, Journal of Mathematical Biology, 1997, 36(2), 149-168. doi: 10.1007/s002850050095 [7] M. Das, A. Maiti and G. P. Samanta, Stability analysis of a prey-predator fractional order model incorporating prey refuge, Ecological Genetics and Genomics, 2018, 7, 33-46. [8] R. P. Gupta, M. Banerjee, and P. Chandra, Period doubling cascades of prey-predator model with nonlinear harvesting and control of over exploitation through taxation, Communications in Nonlinear Science & Numerical Simulation, 2014, 19(7), 2382-2405. [9] B. D. Hassard, N. D. Kazarinoff and Y. Wan, Theory and Applications of Hopf Bifurcation, Cambridge: Cambridge University Press, 1981. [10] S. B. Hsu and T. W. Hwang, Uniqueness of limit cycles for a predator-prey system of Holling and Leslie type, Canadian Applied Mathematics Quarterly, 1998, 6(2), 91-117. [11] T. K. Kar and H. Matsuda, Global dynamics and controllability of a harvested prey-predator system with Holling type III functional response, Nonlinear Analysis: Hybrid Systems, 2007, 1(1), 59-67. doi: 10.1016/j.nahs.2006.03.002 [12] T. K. Kar and A. Batabyal, Stability and bifurcation of a prey-predator model with time delay, Comptes Rendus Biologies, 2009, 332(7), 642-651. doi: 10.1016/j.crvi.2009.02.002 [13] Y. Kuang and Y. Takeuchi, Predator-prey dynamics in models of prey dispersal in two-patch environments, Mathematical Bioences, 1994, 120(1), 77-98. £ [14] T. K. Kar and U. K. Pahari, Non-selective harvesting in preyšCpredator models with delay, Communications in Nonlinear Science & Numerical Simulation, 2006, 11(4), 499-509. [15] T. K. Kar and S. Jana, Stability and bifurcation analysis of a stage structured predator prey model with time delay, Applied Mathematics & Computation, 2012, 219(8), 3779-3792. £ [16] A. J. Lotka, Elements of mathematical biology, Econometrica, 1956. [17] F. Lian and Y. Xu, Hopf bifurcation analysis of a predator-prey system with Holling type IV functional response and time delay, Applied Mathematics and Computation, 2009, 215(4), 1484-1495. doi: 10.1016/j.amc.2009.07.003 [18] Y. Li and D. Xiao, Bifurcations of a predator-prey system of Holling and Leslie types, Chaos, Solitons & Fractals, 2007, 34(2), 606-620. [19] Z. Ma, H. Tang, S. Wang and T. Wang, Bifurcation of a Predator-prey System with Generation Delay and Habitat Complexity, Journal of the Korean Mathematical Society, 2018, 55(1), 43-58. [20] A. F. Nindjin, M. A. Aziz-Alaoui and M. Cadivel, Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay, nonlinear analysis real world applications, 2006, 7(5), 1104-1118. ££ doi: 10.1016/j.nonrwa.2005.10.003 [21] X. Rui and L. Chen, Persistence and stability for a two-species ratio-dependent predator-prey system with time delay in a two-patch environment, Computers & Mathematics with Applications, 2000, 40(4-5), 577-588. [22] J. F. Savino and R. A. Stein, Behavioural interactions between fish predators and their prey: effects of plant density, Animal Behaviour, 1989, 37(1), 311-321. [23] Y. Song and S. Yuan, Bifurcation analysis in a predator-prey system with time delay, Nonlinear Analysis Real World Applications, 2006, 7(2), 265-284. doi: 10.1016/j.nonrwa.2005.03.002 [24] Y. Song and J. Wei, Local Hopf bifurcation and global periodic solutions in a delayed predator-prey system, Journal of Mathematical Analysis & Applications, 2005, 301(1), 1-21. [25] J. Wu, Theory and Applications of Partial Functional Differential Equations, NewYork: Springer-Verlag, 1996. [26] X. Wang and J. Wei, Dynamics in a diffusive predator-prey system with strong Allee effect and Ivlev-type functional response, Journal of Mathematical Analysis and Applications, 2015, 422, 1447-1462. doi: 10.1016/j.jmaa.2014.09.051 [27] F. Yi, J. Wei and J. Shi, Bifurcation and Spatiotemporal Patterns in a Homoge-neous Diffusive Predator-prey System, Journal of Differential Equations, 2009, 246(5), 1944-1977. doi: 10.1016/j.jde.2008.10.024 [28] X. Yan and W. Li, Stability and Hopf bifurcation for a delayed prey-predator system with diffusion effects, Applied Mathematics and Computation, 2008, 192(2), 552-566. [29] F. Zhang, Y. Chen and J. Li, Dynamical analysis of a stage-structured predator-prey model with cannibalism, Mathematical Bioences, 2019, 307, 33-41. -
-
Figures(5)
Export File
Citation
Haicheng Liu, Bin Ge, Qiyuan Liang, Jiaqi Chen. A DELAYED SEMILINEAR PARABOLIC PREDATOR-PREY SYSTEM WITH HABITAT COMPLEXITY AND HARVESTING EFFECTS[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2561-2582. doi: 10.11948/20210015
Format
Content
DownLoad:
-
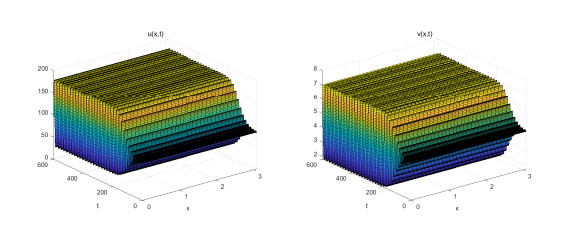
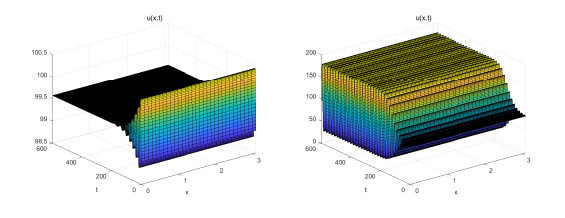
Figure 1.
$ {{P}^{*}} = (99.568, 4.825) $ is locally asymptotically stable, and the initial value is$ (99.5, 4.8) $ . -
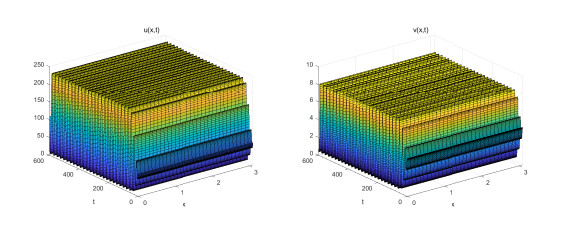
Figure 2. The system produces periodic solutions, and the initial value is
$ (82.9, 4.4) $ . -
Figure 3. The system produces spatially homogeneous periodic solutions, and the initial value is
$ (62.2, 4.2) $ . -
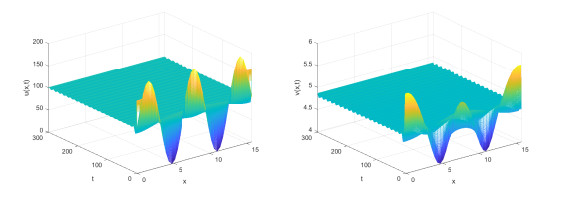
Figure 4.
$ \tau = 1<{{\tau }_{0}} $ , the system is locally asymptotically stable at$ {{P}^{*}} = ({{u}_{0}}, {{v}_{0}}) $ . -
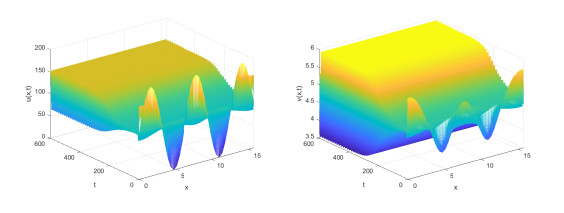
Figure 5.
$ \tau = 1.2>{{\tau }_{0}} $ , the system produces periodic solutions at$ {{P}^{*}} = ({{u}_{0}}, {{v}_{0}}) $ .