| Citation: |
Zhenjie Niu, Zenggui Wang. BIFURCATION AND EXACT TRAVELING WAVE SOLUTIONS FOR THE GENERALIZED NONLINEAR DISPERSIVE MK(M, N) EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2866-2875. doi: 10.11948/20210023
|
BIFURCATION AND EXACT TRAVELING WAVE SOLUTIONS FOR THE GENERALIZED NONLINEAR DISPERSIVE MK(M, N) EQUATION
-
Abstract
This paper investigated the generalized nonlinear dispersive mK(m, n) equation by the planar dynamical systems method, the bifurcations of the system with different parameter region of this equation are presented. Moreover, we find different kinds of exact explicit solutions like peak type solutions, periodic wave solutions and valley type solutions.
-
-
References
[1] M. M. Arab, A (3+1)-dimensional nonlinear extended Zakharov-Kuznetsov dynamical equation: Bifurcation and traveling wave solutions, AIP Advances, 2020, 10(12), Article ID: 125310. doi: 10.1063/5.0029328 [2] S. N. Chow and J. K. Hale, Methods of bifurcation theory[J]. Grundlehren Der Mathematischen Wissenschaften, 1990, 24(18), 36-40. [3] M. Chu, B. Tian, H. Yin, et al., Kink soliton solutions and bifurcation for a nonlinear space-fractional Kolmogorov-Petrovskii-Piskunov equation in circuitry, chemistry or biology, Modern Physics Letters B, 2019, 33(30), Article ID: 1950372. doi: 10.1142/S021798491950372X [4] A. Das, N. Ghosh and K. Ansari, Bifurcation and exact traveling wave solutions for dual power Zakharov-Kuznetsov-Burgers equation with fractional temporal evolution, Computers & Mathematics with Applications, 2018, 75(1), 59-69. [5] Z. Dai and Y. Xu, Bifurcations of traveling wave solutions and exact solutions to generalized Zakharov equation and Ginzburg-Landau equation, Applied Mathematics & Mechanics, 2011, 32(12), 1615-1622. [6] A. A. Elmandouh, Integrability, qualitative analysis and the dynamics of wave solutions for Biswas-Milovic equation, European Physical Journal Plus, 2021, 136(6). doi: 10.1140/epjp/s13360-021-01626-2 [7] A. A. Elmandouh, Bifurcation and new traveling wave solutions for the 2D Ginzburg-Landau equation, The European Physical Journal Plus, 2020, 135(8), 1-13. doi: 10.1140/epjp/s13360-020-00675-3 [8] M. E. Elbrolosy and A. A. Elmandouh, Bifurcation and new traveling wave solutions for (2+1)-dimensional nonlinear Nizhnik-Novikov-Veselov dynamical equation, European Physical Journal Plus, 2020, 135(6), 1-11. doi: 10.1140/epjp/s13360-020-00546-x [9] A. Galves, J. K. Hale and C. Rocha, Differential equations and dynamical systems, Springer-Verlag, 1991. [10] B. He, Q. Meng, W. Rui and L. Yao, Bifurcations of travelling wave solutions for the mK(n, n) equation, Communications in Nonlinear Science and Numerical Simulation, 2008, 13, 2114-2123. doi: 10.1016/j.cnsns.2007.06.006 [11] B. He and Q. Meng, Bifurcations and new exact travelling wave solutions for the Gerdjikov-CIvanov equation, Communications in Nonlinear Science & Numerical Simulation, 2010, 15(7), 1783-1790. [12] S. Lai, J. He and Y. Qing, A new study for the modified nonlinear dispersive mK(m, n) equations in higher dimensional spaces, International Journal of Pure and Applied Mathematics, 2009, 51(1), 1-9. [13] J. Li and T. He, Exact traveling wave solutions and bifurcations in a nonlinear elastic rod equation, Acta Mathematicae Applicatae Sinica(English Series), 2010, 26(2), 283-306. doi: 10.1007/s10255-008-8139-1 [14] J. Li, Bifurcations of travelling wave solutions for two generalized Boussinesq systems, Sci. China Ser. A: Math., 2008, 51(009), 1577-1592. doi: 10.1007/s11425-008-0038-7 [15] T. D. Leta and J. Li, Various Exact Soliton Solutions and Bifurcations of a Generalized Dullin-Gottwald-Holm Equation with a Power Law Nonlinearity, International Journal of Bifurcation and Chaos, 2017, 27(08), Article ID: 1750129. doi: 10.1142/S0218127417501292 [16] T. D. Leta, W. Liu, A. E. Achab, et al., Dynamical Behavior of Traveling Wave Solutions for a (2+1)-Dimensional Bogoyavlenskii Coupled System, Qualitative Theory of Dynamical Systems, 2021, 20(1). doi: 10.1007/s12346-021-00449-x [17] Q. Meng, W. Li and B. He, Smooth and peaked solitary wave solutions of the Broer-Kaup System using the approach of dynamical system, Communications in Theoretical Physics, 2014, 62(3), 308-314. doi: 10.1088/0253-6102/62/3/03 [18] M. A. Nuwairan and A. A. Elmandouh, Qualitative analysis and wave propagation of the nonlinear model for low-pass electrical transmission lines, Physica Scripta, 2021, 96(9), 15, Article ID: 095214. [19] P. Rosenau and J. M. Hyman, Compactons: solitons with finite wavelength, Physical Review Letters, 1993, 70(5), 564-567. doi: 10.1103/PhysRevLett.70.564 [20] A. M. Wazwaz, General compactons solutions and solitary patterns solutions for modified nonlinear dispersive equations mK(n, n) in higher dimensional spaces, Mathematics & Computers in Simulation, 2002, 59(6), 519-531. [21] Z. Wen, The generalized bifurcation method for deriving exact solutions of nonlinear space-time fractional partial differential equations, Applied Mathematics and Computation, 2020, 366, Article ID: 124735. doi: 10.1016/j.amc.2019.124735 [22] Z. Yan, Modified nonlinearly dispersive mK(m, n, k) equations: Ⅰ. New compacton solutions and solitary pattern solutions, Computer Physics Communications, 2003, 152(1), 25-33. doi: 10.1016/S0010-4655(02)00794-4 [23] B. Zhang, Y. Xia, W. Zhu, et. al, Explicit exact traveling wave solutions and bifurcations of the generalized combined double sinhšCcosh-Gordon equation, Applied Mathematics and Computation, 2019, 363, Article ID: 124576. -
-
Figures(6)
Export File
Citation
Zhenjie Niu, Zenggui Wang. BIFURCATION AND EXACT TRAVELING WAVE SOLUTIONS FOR THE GENERALIZED NONLINEAR DISPERSIVE MK(M, N) EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2866-2875. doi: 10.11948/20210023
Format
Content
DownLoad:
-
Figure 1. The bifurcation set of system(1.2).(a)
$ m-n = 2k+1 $ is odd; (b)$ m-n = 2k+2 $ is even -
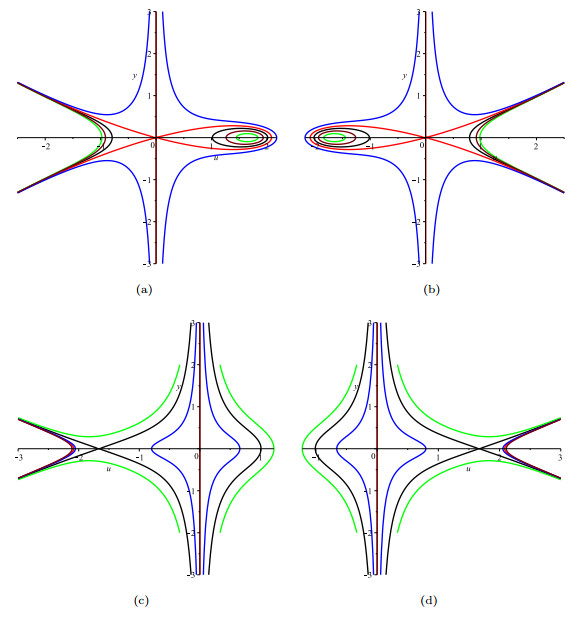
Figure 2. The phase portraits of system (2.5) with
$ m-n = 2k+1 $ . (a)$ a>0, c>0 $ ; (b)$ a<0, c>0 $ ; (c)$ a>0, c<0 $ ; (d)$ a<0, c<0 $ - Figure 3. The phase portraits of system (2.5) with m − n = 2k. (a) a > 0, c > 0;(b) a < 0, c > 0; (c) a > 0, c < 0; (d) a < 0, c < 0
-
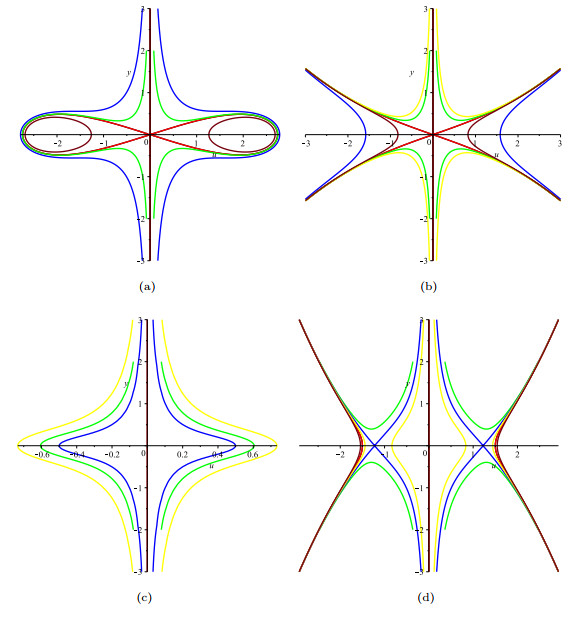
Figure 4. The phase portraits of system (2.5) with
$ m-n = 2k+1 $ . (a)$ (c, g)\in A(1) $ ; (b)$ (c, g)\in A(2) $ ; (c)$ (c, g)\in A(3) $ ; (d)$ (c, g)\in A(4) $ ; (e)$ (c, g)\in A(5) $ ; (f)$ (c, g)\in A(6) $ -
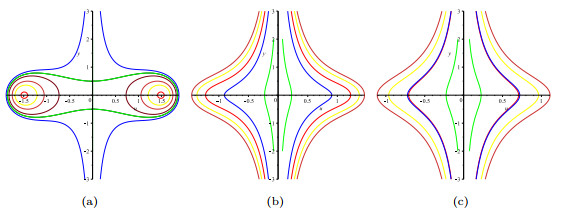
Figure 5. The phase portraits of system (2.5) with
$ m-n = 2k+2 $ . (a)$ (c, g)\in $ B(1); (b)$ (c, g)\in $ B(2); (c)$ (c, g)\in $ B(3) -
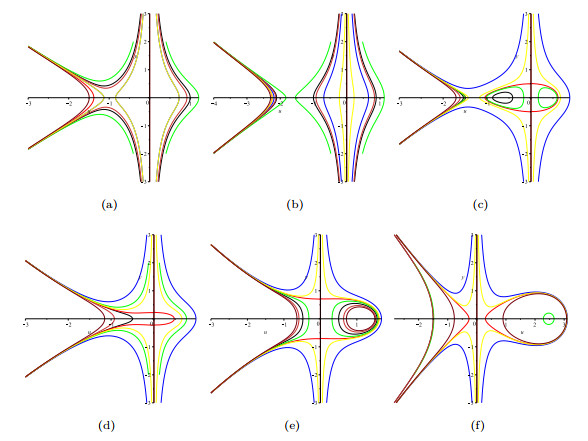
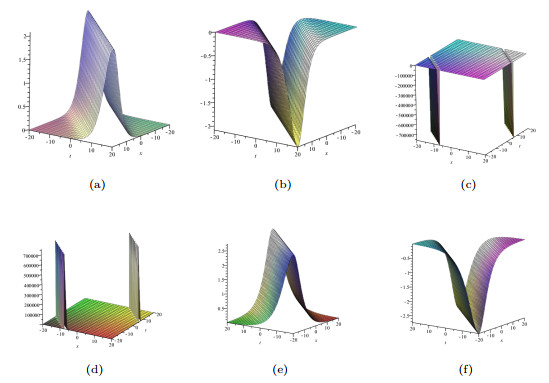
Figure 6. (a) solution(3.1) when
$ a>0 $ ; (b) solution (3.1) when$ a<0 $ ; (c) solution (3.2) when$ a>0 $ ; (d) solution (3.2) when$ a<0 $ ; (e) solution (3.3) when$ u(\xi)>0 $ ; (f) solution (3.3) when$ u(\xi)<0 $