| Citation: |
Rongyan Wang, Wencai Zhao. EXTINCTION AND STATIONARY DISTRIBUTION OF A STOCHASTIC PREDATOR-PREY MODEL WITH HOLLING Ⅱ FUNCTIONAL RESPONSE AND STAGE STRUCTURE OF PREY[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 50-68. doi: 10.11948/20210028
|
EXTINCTION AND STATIONARY DISTRIBUTION OF A STOCHASTIC PREDATOR-PREY MODEL WITH HOLLING Ⅱ FUNCTIONAL RESPONSE AND STAGE STRUCTURE OF PREY
-
Abstract
The interaction between predator and prey is an important part of ecological diversity. This paper presents a stage-structured predator-prey model to study how stochastic environments affect population dynamics. Holling Ⅱ functional response is also incorporated in the proposed theoretical framework. Specifically, by using the theory of stochastic stability, we provide conditions for the stochastic system to suffer extinction or to have a unique ergodic stationary distribution. Besides, numerical simulations are also employed to verify the validity of the theoretical results.
-
-
References
[1] C. Arora and V. Kumar, Bifurcation analysis of a delayed modified Holling-Tanner predator-prey model with refuge, in International Conference on Mathematics and Computing, Springer, 2017, 246-254. [2] L. K. Beay, A. Suryanto, I. Darti et al., Hopf bifurcation and stability analysis of the Rosenzweig-MacArthur predator-prey model with stage-structure in prey, Mathematical Biosciences and Engineering, 2020, 17(4), 4080-4097. doi: 10.3934/mbe.2020226 [3] A. Berman and R. J. Plemmons, Nonnegative matrices in the mathematical sciences, SIAM, 1994. [4] Y. Cai, J. Li, Y. Kang et al., The fluctuation impact of human mobility on the influenza transmission, Journal of the Franklin Institute, 2020, 357(13), 8899-8924. doi: 10.1016/j.jfranklin.2020.07.002 [5] Z. Chang, X. Meng and T. Zhang, A new way of investigating the asymptotic behaviour of a stochastic SIS system with multiplicative noise, Applied Mathematics Letters, 2019, 87, 80-86. doi: 10.1016/j.aml.2018.07.014 [6] L. Chen, L. Chen and L. Zhong, Permanence of a delayed discrete mutualism model with feedback controls, Mathematical and Computer Modelling, 2009, 50(7-8), 1083-1089. doi: 10.1016/j.mcm.2009.02.015 [7] J. M. Drake, Elements of mathematical ecology, 2002, 50(3), 205-207. [8] T. Feng, D. Charbonneau, Z. Qiu and Y. Kang, Dynamics of task allocation in social insect colonies: scaling effects of colony size versus work activities, Journal of Mathematical Biology, 2021, 82(5), 1-53. [9] T. Feng, Z. Qiu and Y. Kang, Recruitment dynamics of social insect colonies, SIAM Journal on Applied Mathematics, 2021, 81(4), 1579-1599. doi: 10.1137/20M1332384 [10] T. Feng, Z. Qiu and X. Meng, Analysis of a stochastic recovery-relapse epidemic model with periodic parameters and media coverage, Journal of Applied Analysis and Computation, 2019, 9(3), 1007-1021. doi: 10.11948/2156-907X.20180231 [11] D. J. Higham, An algorithmic introduction to numerical simulation of stochastic differential equations, SIAM Review, 2001, 43(3), 525-546. doi: 10.1137/S0036144500378302 [12] L. Imhof and S. Walcher, Exclusion and persistence in deterministic and stochastic chemostat models, Journal of Differential Equations, 2005, 217(1), 26-53. doi: 10.1016/j.jde.2005.06.017 [13] E. M. Kafi and A. A. Majeed, The dynamics and analysis of stage-structured predator-prey model involving disease and refuge in prey population, in Journal of Physics: Conference Series, 1530, 2020, 012036. [14] S. Li and J. Wu, Qualitative analysis of a predator-prey model with predator saturation and competition, Acta Applicandae Mathematicae, 2016, 141(1), 165-185. doi: 10.1007/s10440-015-0009-2 [15] M. Liu, C. Du and M. Deng, Persistence and extinction of a modified Leslie–-Gower Holling-type Ⅱ stochastic predator-–prey model with impulsive toxicant input in polluted environments, Nonlinear Analysis Hybrid Systems, 2018, 27, 177-190. doi: 10.1016/j.nahs.2017.08.001 [16] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Dynamics of a stochastic predator-prey model with stage structure for predator and Holling type Ⅱ functional response, Journal of Nonlinear Science, 2018, 28(3), 1151-1187. doi: 10.1007/s00332-018-9444-3 [17] X. Ma, Y. Shao, Z. Wang et al., An impulsive two-stage predator-prey model with stage-structure and square root functional responses, Mathematics and Computers in Simulation, 2016, 119, 91-107. doi: 10.1016/j.matcom.2015.08.009 [18] X. Mao, Stochastic differential equations and applications, Elsevier, 2007. [19] S. G. Mortoja, P. Panja and S. K. Mondal, Dynamics of a predator-prey model with stage-structure on both species and anti-predator behavior, Informatics in Medicine Unlocked, 2018, 10, 50-57. doi: 10.1016/j.imu.2017.12.004 [20] H. Qi, X. Meng and T. Zhang, Periodic solution and ergodic stationary distribution of SEIS dynamical systems with active and latent patients, Qualitative Theory of Dynamical Systems, 2018, 43(1), 347-369. [21] S. Sadhu and C. Kuehn, Stochastic mixed-mode oscillations in a three-species predator-prey model, Chaos, 2018, 28(3), 033606. doi: 10.1063/1.4994830 [22] L. Wang and R. Xu, Global stability of a predator-prey model with stage structure, Chinese Quarterly Journal of Mathematics, 2015, 30(1), 107-120. [23] C. Xu, Y. Yu and G. Ren, Dynamic analysis of a stochastic predator-prey model with Crowley-Martin functional response, disease in predator, and saturation incidence, Journal of Computational and Nonlinear Dynamics, 2020, 15(7), 071004. doi: 10.1115/1.4047085 [24] C. Xu, S. Yuan and T. Zhang, Stochastic sensitivity analysis for a competitive turbidostat model with inhibitory nutrients, International Journal of Bifurcation and Chaos, 2016, 26(10), 707-723. [25] C. Xu, S. Yuan and T. Zhang, Average break-even concentration in a simple chemostat model with telegraph noise, Nonlinear Analysis Hybrid Systems, 2018, 29, 373-382. doi: 10.1016/j.nahs.2018.03.007 [26] D. Xu, M. Liu and X. Xu, Analysis of a stochastic predator-prey system with modified Leslie-Gower and Holling-type Ⅳ schemes, Physica A: Statistical Mechanics and its Applications, 2020, 537, 122761. doi: 10.1016/j.physa.2019.122761 [27] J. Xu, T. Zhang and K. S, A stochastic model of bacterial infection associated with neutrophils, Applied Mathematics and Computation, 2020, 373(12), 125025. [28] L. Yang, K. A. Pawelek and S. Liu, A stage-structured predator-prey model with predation over juvenile prey, Applied Mathematics and Computation, 2017, 297, 115-130. doi: 10.1016/j.amc.2016.10.035 [29] Y. Yao, Bifurcations of a Leslie-Gower prey-predator system with ratio-dependent Holling Ⅳ functional response and prey harvesting, Mathematical Methods in the Applied Sciences, 2020, 43(5), 2137-2170. doi: 10.1002/mma.5944 [30] X. Yu, S. Yuan and T. Zhang, The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms, Nonlinear Dynamics, 2018, 91, 1653-1668. doi: 10.1007/s11071-017-3971-6 [31] X. Yu, S. Yuan and T. Zhang, Asymptotic properties of stochastic nutrient-plankton food chain models with nutrient recycling, Nonlinear Analysis: Hybrid Systems, 2019, 34, 209-225. doi: 10.1016/j.nahs.2019.06.005 [32] T. Zhang, Z. Chen and M. Han, Dynamical analysis of a stochastic model for cascaded continuous flow bioreactors, Journal of Mathematical Chemistry, 2014, 52(5), 1441-1459. doi: 10.1007/s10910-014-0321-5 [33] X. Zhang, The global dynamics of stochastic Holling type Ⅱ predator-prey models with non constant mortality rate, Filomat, 2017, 31(18), 5811-5825. doi: 10.2298/FIL1718811Z [34] X. Zhang, L. Chen and A. U. Neumann, The stage-structured predator-prey model and optimal harvesting policy, Mathematical Biosciences, 2000, 168(2), 201-210. doi: 10.1016/S0025-5564(00)00033-X [35] J. Zhou and C. Mu, Coexistence of a diffusive predator-prey model with Holling type-Ⅱ functional response and density dependent mortality, Journal of Mathematical Analysis and Applications, 2012, 385(2), 913-927. doi: 10.1016/j.jmaa.2011.07.027 [36] Y. Zhou, W. Sun, Y. Song et al., Hopf bifurcation analysis of a predator-prey model with Holling-Ⅱ type functional response and a prey refuge, Nonlinear Dynamics, 2019, 97(2), 1439-1450. doi: 10.1007/s11071-019-05063-w [37] F. Zhu, X. Meng and T. Zhang, Optimal harvesting of a competitive n-species stochastic model with delayed diffusions, Mathematical Biosciences and Engineering, 2019, 16(3), 1554-1574. doi: 10.3934/mbe.2019074 -
-
Figures(3)
Export File
Citation
Rongyan Wang, Wencai Zhao. EXTINCTION AND STATIONARY DISTRIBUTION OF A STOCHASTIC PREDATOR-PREY MODEL WITH HOLLING Ⅱ FUNCTIONAL RESPONSE AND STAGE STRUCTURE OF PREY[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 50-68. doi: 10.11948/20210028
Format
Content
DownLoad:
-
Figure 1. Three pictures in the left column are the paths of
$ x_{1},x_{2},y $ of system$ (1.3) $ with the initial value$ (0.1,0.1,0.1) $ under the noise intensities$ \sigma_{1}^{2} = 0.004, \sigma_{2}^{2} = 0.01, \sigma_{3}^{2} = 0.01 $ . The red lines mean the solution of$ (1.3) $ and the green lines mean the solution of the corresponding undisturbed system$ (1.2) $ . Three in the right column show the histograms of the probability density functions of$ x_{1},x_{2},y $ . The seventh is the corresponding phase diagram, revealing the interplay of the three populations in phase space. -
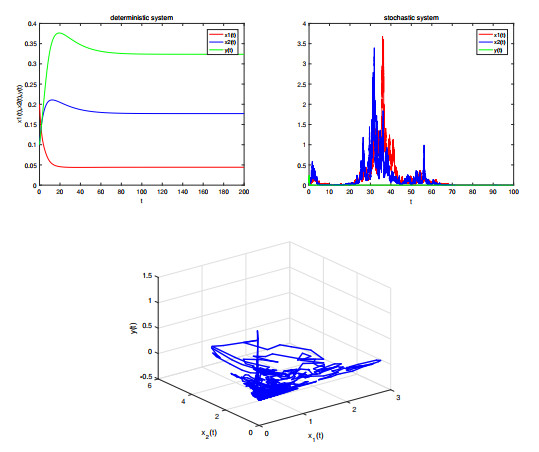
Figure 2. The left figure above shows the paths of
$ x_{1},x_{2},y $ of the deterministic system$ (1.2) $ with initial value$ (0.1,0.1,0.1) $ . The right above is the paths of the corresponding stochastic system$ (1.3) $ under$ \sigma_{1}^{2} = 0.45,\sigma_{2}^{2} = 1.5,\sigma_{3}^{2} = 8 $ . The third is the corresponding phase diagram, which displays the interplay of the three populations in phase space. -
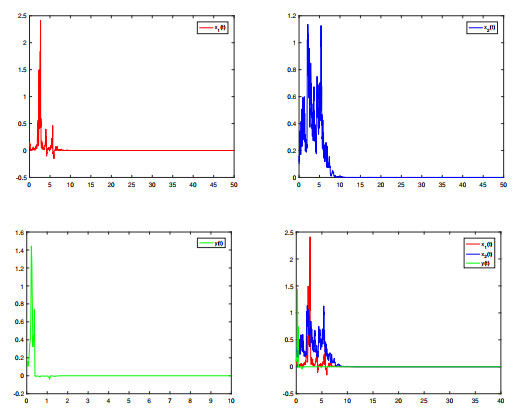
Figure 3. The paths of
$ x_{1},x_{2},y $ of system$ (1.3) $ with the initial value$ (0.1,0.1,0.1) $ under$ \sigma_{1}^{2} = 9.2,\sigma_{2}^{2} = 2,\sigma_{3}^{2} = 9 $ , which shows that preys and predators are extinguish.