| Citation: | Fangfang Jiang. EXISTENCE AND UNIQUENESS OF DISCONTINUOUS PERIODIC ORBITS IN SECOND ORDER DIFFERENTIAL EQUATIONS WITH STATE-DEPENDENT IMPULSES[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 69-86. doi: 10.11948/20210029 |
EXISTENCE AND UNIQUENESS OF DISCONTINUOUS PERIODIC ORBITS IN SECOND ORDER DIFFERENTIAL EQUATIONS WITH STATE-DEPENDENT IMPULSES
-
Abstract
In this paper, we are concerned with the existence and uniqueness of discontinuous periodic orbits for a class of second order impulsive differential equations with state-dependent jumps. we apply geometric method to estimate the time mapping of the equation, and then by using Poincaré-Bohl fixed point theorem to obtain some existence criteria under assumptions that the nonlinear term satisfies linear growth conditions. And, the uniqueness of the discontinuous periodic orbit is further proved. Finally, several specific impulsive functions are presented in examples to illustrate the obtained results.
-

-
References
[1] D. Bainov and P. Simenov, Impulsive Differential Equations: Periodic Solutions and Applications, Longman Scientific and Technical, Essex, England, 1993. [2] E. Bonotto, Flows of Characteristic in Impulsive Semidynamical Systems, J. Math. Anal. Appl., 2007, 332, 81-96. doi: 10.1016/j.jmaa.2006.09.076 [3] S. Balasuriya, Impulsive Perturbations to Differential Equations: Stable/Unstable Pseudo-Manifolds, Heteroclinic Connections, and Flux, Nonlinearity, 2016, 29(12), 3897-3933. doi: 10.1088/0951-7715/29/12/3897 [4] L. Chen, Theory and Application of Semicontinuous Dynamical System, J. YuLin Nomal University (Natural Science), 2013, 34(2), 2-10. [5] L. Chen, Applications of the Moser's Twist Theorem to Some Impulsive Differential Equations, Qual. Theor. Dyn. Syst., 2020, 19(2), 1-20. [6] K. Ciesielski, On Semicontinuity in Impulsive Systems, Bull Polish Acad Sci Math., 2004, 52, 71-80. doi: 10.4064/ba52-1-8 [7] T. Ding, Applications of Qualitative Methods of Ordinary Differential Equations, China Higher Education Press, Beijing, 2004. [8] T. Ding, R. Iannacci and F. Zanolin, Existence and Multiplicity Results for Periodic Solutions of Semilinear Duffing Equations, J. Diff. Eqs., 1993, 105, 364-409. doi: 10.1006/jdeq.1993.1093 [9] T. Ding and F. Zanolin, Periodic Solutions of Duffing's Equations with Superquadratic Potential, J. Diff. Eqs., 1992, 97, 328-378. doi: 10.1016/0022-0396(92)90076-Y [10] T. Ding, An Infinite Class of Periodic Solutions of Periodically Perturbed Duffing Equations at Resonance, Proc. Amer. Math. Soc., 1982, 86(1), 47-54. doi: 10.1090/S0002-9939-1982-0663864-1 [11] Z. Hu and M. Han, Periodic Solutions and Bifurcations of First-order Impulsive Differential Equations, Internat. J. Bifur. Chaos, 2009, 19(8), 2515-2530. doi: 10.1142/S0218127409024281 [12] F. Jiang, D. W. Lu and J. Sun, Periodic Orbits Analysis in a Class of Planar Liénard Systems with State-Triggered Jumps, Internat. J. Bifur. Chaos, 2016, 26(9), Article ID 1650153. [13] F. Jiang, Existence of Periodic Solutions in Impulsive Differential Equations, J. Nonlinear Model. Anal., 2021, 3(1), 53-70. [14] S. Kaul, On Impulsive Semidynamical Systems, J. Math. Anal. Appl., 1990, 150(1), 120-128. doi: 10.1016/0022-247X(90)90199-P [15] V. Lakshmikantham, D. Bainov and P. Simeonov, Theory of Impulsive Differential Equations, World Scientific, Singapore, 1989. [16] J. Llibre, M. Ord$\acute{o}$nez and E. Ponce, On the Existence and Uniqueness of Limit Cycles in Planar Continuous Piecewise Linear Systems without Symmetry, Nonlinear Anal: Real, 2013, 14, 2002-2012. [17] Y. Niu and X. Li, Periodic Solutions of Semilinear Duffing Equations with Impulsive Effects, J. Math. Anal. Appl., 2018, 467(1), 349-370. doi: 10.1016/j.jmaa.2018.07.008 [18] Y. Niu and X. Li, An Application of Moser's Twist Theorem to Superlinear Impulsive Differential Equations, Discrete Cont. Dyn-A, 2019, 39(1), 431-445. doi: 10.3934/dcds.2019017 [19] D. Qian, L. Chen and X. Sun, Periodic Solutions of Superlinear Impulsive Differential Equations: A Geometric Approach, J. Diff. Eqs., 2015, 259(6), 3088-3106. [20] D. Qian, P. J. Torres and P. Wang, Periodic Solutions of Second Order Equations via Rotation Numbers, J. Diff. Eqs., 2019, 266, 4746-4768. doi: 10.1016/j.jde.2018.10.010 [21] D. Qian and P. J. Torres, Periodic Motions of Linear Impact Oscillators Via the Successor Map, SIAM J. Math. Anal., 2005, 36, 1707-1725. doi: 10.1137/S003614100343771X [22] C. Rebelo and F. Zanolin, Multiplicity Results for Periodic Solutions of Second Order ODEs with Asymmetric Nonlinearities, Trans. Amer. Math. Soc., 1996, 348, 2349-2389. doi: 10.1090/S0002-9947-96-01580-2 [23] J. Shen, L. Chen and X. Yuan, Lagrange Stability for Impulsive Duffing Equations, J. Diff. Eqs., 2019, 266(11), 6924-6962. doi: 10.1016/j.jde.2018.11.022 [24] D. Wang, On the Existence of $2\pi$-Periodic Solutions of a Differential Equation $x"+g(x)=p(t)$, Ann. Math., 1984, 5A(1), 61-72. [25] X. Wang, D. Qian and X. Sun, Periodic Solutions of Second Order Equations with Asymptotical Nonresonance, Discrete Cont. Dyn-A, 2018, 38(9), 4715-4726. doi: 10.3934/dcds.2018207 [26] Z. Wang, Periodic Solutions of the Second Order Differential Equations with Lipschitzian Condition, Proc. Amer. Math. Soc., 1998, 2267-2276. [27] G. Zeng, L. Chen and L. Sun, Existence of Periodic Solution of Order-one of Planar Impulsive Autonomous System, J. Comput. Appl. Math., 2006, 186, 466-481. doi: 10.1016/j.cam.2005.03.003 [28] G. Zeng, F. Wang and J. Nieto, Complexity of a Delayed Predator-Prey Model with Impulsive Harvest and Holling-Type Ⅱ Functional Response, Adv. Complex Syst., 2008, 11, 77-97. doi: 10.1142/S0219525908001519 [29] H. Zhang, L. Chen and J. Nieto, A Delayed Epidemic Model with Stage Structure and Pulses for Management Strategy, Nonlinear Anal: Real, 2008, 9, 1714-1726. doi: 10.1016/j.nonrwa.2007.05.004 -
-
-
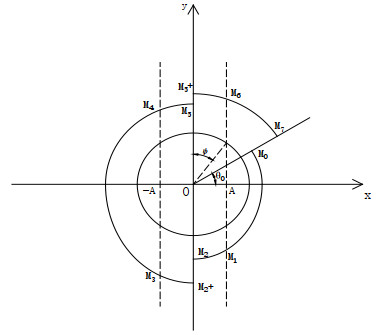
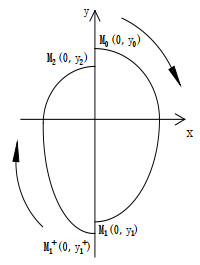
Figure 1. A discontinuous periodic orbit which starts from the point
$ M_0 $ and rotates clockwise a circle on the$ (x,y) $ -plane:$ M_0(0,y_0)\xrightarrow{P_R}M_1(0,y_1)\xrightarrow{\Phi}M_1^+(0,y_1^+)\xrightarrow{P_L}M_2(0,y_2)\xrightarrow{\Phi}M_0(0,y_0) $ , where$ y_1 = -p_R(y_0) $ ,$ \Phi(M_1) = M_1^+ $ ,$ y_1^+ = -p_R(y_0)+J(-p_R(y_0)) $ ,$ y_2 = p_L(p_R(y_0)-J(-p_R(y_0))) $ ,$ \Phi(M_2) = M_0 $ . - Figure 2. Schematic diagram
-
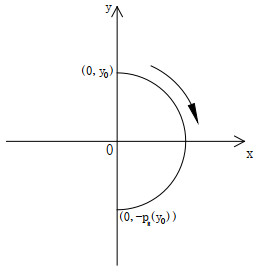
Figure 3. Schematic diagram:
$ (0,y_0)\xrightarrow{P_R}(0,-p_R(y_0))\xrightarrow{\Phi}(0,y_0) $ . -
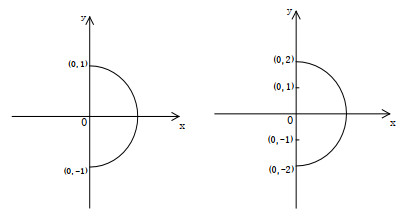
Figure 4. Left:
$ \Phi(0,-1) = (0,1) $ ; Right:$ \Phi(\Phi(0,-2)) = (0,2) $ .




 DownLoad:
DownLoad: