| Citation: |
Chun Lu, Xiaohua Ding, Lei Zhang. STATIONARY DISTRIBUTION AND PERMANENCE OF A STOCHASTIC DELAY PREDATOR-PREY LOTKA-VOLTERRA MODEL WITH LÉVY JUMPS[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1328-1352. doi: 10.11948/20210077
|
STATIONARY DISTRIBUTION AND PERMANENCE OF A STOCHASTIC DELAY PREDATOR-PREY LOTKA-VOLTERRA MODEL WITH LÉVY JUMPS
-
Abstract
In this paper, we propose and investigate an impulsive stochastic predator-prey Lotka-Volterra model with infinite delay and Lévy jumps. Sufficient criteria for permanence in time average and the threshold between stability in time average and extinction are provided. For the corresponding case without impulse, the easily substantiated sufficient criteria for stability in distribution are derived. Our results demonstrate that, first of all, the coefficients related to infinite delay have some effects on permanence in time average and stability in distribution; then impulsive perturbations play a prominent part in keeping the permanence in time average despite the unfavourable factor Lévy jumps causes.
-
-
References
[1] I. Barǎalat, Systems d'equations differential d'oscillations nonlineairies, Rev. Roumaine Math. Pures Appl., 1959, 4, 267-270. [2] J. Bao, X. Mao, G. Yin and C. Yuan, Competitive Lotka-Volterra population dynamics with jumps, Nonlinear Anal., 2011, 74, 6601-6616. doi: 10.1016/j.na.2011.06.043 [3] O. Butkovsky and M. Scheutzow, Invariant measures for stochastic functional differential equations, Electron. J. Probab., 2017, 22, 1-23. [4] J. Bao, G. Yin and C. Yuan, Stationary distributions for retarded stochastic differential equations without dissipativity, Stochastics, 2017, 89, 530-549. doi: 10.1080/17442508.2016.1267180 [5] Z. Chang, X. Xing, S. Liu and X. Meng, Spatiotemporal dynamics for an impulsive eco-epidemiological system driven by canine distemper virus, Appl. Math. Comput., 2021, 402, 126135. [6] N. H. Du, N. H. Dang and N. T. Dieu, On stability in distribution of stochastic differential delay equations with markovian switching, Syst. Control Lett., 2014, 65, 43-49. [7] K. Gopalsamy, Stability and Oscillation in Delay Differential Equations of Population Dynamics, Kluwer Academic, 1992. [8] R. Has'minskii, Stochastic Stability of Differential Equations, Sijthoff and Noordhoff, Alphen aan den Rijn, The Netherlands, 1980. [9] D. J. Higham, An algorithmic introduction to numerical simulation of stochastic diffrential equations, SIAM Rev., 2001, 43, 525-546. doi: 10.1137/S0036144500378302 [10] Y. Kuang, Delay Differential Equations with Applications in Population Dynamics, Academic Press, 1993. [11] Y. Kuang and H. L. Smith, Global stability for infinite delay Lotka-Volterra type systems, J. Differential Equations., 2003, 103, 221-246. [12] X. Li, G. Song, Y. Xia and C. Yuan, Dynamical behaviors of the tumor-immune system in a stochastic environment, SIAM J. Appl. Math., 2019, 79, 2193-2217. doi: 10.1137/19M1243580 [13] Q. Liu and Q. Chen, Analysis of a general stochastic non-autonomous logistic model with delays and Lévy jumps, J. Math. Anal. Appl., 2016, 433, 95-120. doi: 10.1016/j.jmaa.2015.07.030 [14] X. Li, R. Wang and G. Yin, Moment bounds and ergodicity of switching diffusion systems involving two-time-scale Markov chains, Syst. Control Lett., 2019, 132, Article ID: 104514. doi: 10.1016/j.sysconle.2019.104514 [15] M. Liu and K. Wang, On a stochastic logistic equation with impulsive perturbations, Comput. Math. Appl., 2012, 63, 871-886. doi: 10.1016/j.camwa.2011.11.003 [16] Q. Liu and D. Jiang, Stationary distribution and extinction of a stochastic predator-prey model with distributed delay, Appl. Math, Lett., 2018, 78, 79-87. doi: 10.1016/j.aml.2017.11.008 [17] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Stationary distribution and extinction of a stochastic HIV-1 infection model with distributed delay and logistic Growth, J. Nonlinear Sci., 2020, 30, 369-395. doi: 10.1007/s00332-019-09576-x [18] M. Liu, C. Bai and Y. Jin, Population dynamical behavior of a two-predator one-prey stochastic model with time delay, Discrete Contin. Dyn. Syst., 2017, 37, 2513-2538. doi: 10.3934/dcds.2017108 [19] M. Liu and M. Fan, Stability in distribution of a three-species stochastic casade predator-prey system with time delays, IMA J. Appl. Math., 2017, 82, 396-423. [20] C. Lu, Dynamics of a stochastic Markovian switching predator-prey model with infinite memory and general Lévy jumps, Math. Comput. Simulat., 2021, 181, 316-332. doi: 10.1016/j.matcom.2020.10.002 [21] M. Liu and K. Wang, Stochastic Lotka-Volterra systems with Lévy noise, J. Math. Anal. Appl., 2014, 410, 750-763. doi: 10.1016/j.jmaa.2013.07.078 [22] Q. Liu, D. Jiang, N. Shi, T. Hayat and A. Alsaedi, Stochastic mutualism model with Lévy jumps, Commun. Nonlinear Sci. Numer. Simul., 2017, 43, 78-90. doi: 10.1016/j.cnsns.2016.05.003 [23] C. Lu, Dynamical Behavior of Stochastic Markov Switching Hepatitis B Epidemic Model with Saturated Incidence Rate, J. Funct. Space., 2022, Article ID: 5574983. [24] C. Lu, Dynamical analysis and numerical simulations on a crowley-Martin predator-prey model in stochastic environment, Appl. Math. Comput., 2022, 413, 126641. [25] X. Li and G. Yin, Logistic models with regime switching: Permanence and ergodicity, J. Math. Anal. Appl., 2016, 433, 593-611. [26] M. Liu and C. Bai, Optimal harvesting of a stochastic mutualism model with regime-switching, Appl. Math. Comput., 2020, 37315, Article ID: 125040. [27] X. Li and G. Yin, Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching, J. Math. Anal. Appl., 2011, 376, 11-28. doi: 10.1016/j.jmaa.2010.10.053 [28] L. Liu, X. Meng and T. Zhang, Optimal control strategy for an impulsive stochastic competition system with time delays and jumps, Physica A, 2017, 477, 99-113. doi: 10.1016/j.physa.2017.02.046 [29] G. Lan, S. Yuan and B. Song, The impact of hospital resources and environmental perturbations to the dynamics of SIRS model, J. Frankl. Inst., 2021, 358, 2405-2433. doi: 10.1016/j.jfranklin.2021.01.015 [30] X. Lv, X. Meng and X. Wang, Extinction and stationary distribution of an impulsive stochastic chemostat model with nonlinear perturbation, Chaos Solitons Fractals, 2018, 110, 273-279. doi: 10.1016/j.chaos.2018.03.038 [31] C. Lu and X. Ding, Periodic solutions and stationary distribution for a stochastic predator-prey system with impulsive perturbations, Appl. Math. Comput., 2019, 350, 313-322. [32] C. Lu, G. Sun and Y. Zhang, Stationary distribution and extinction of a multi-stage HIV model with nonlinear stochastic perturbation, J. Appl. Math. Comput., DOI: 10.1007/s12190-021-01530-z. [33] X. Mao, Stochastic Differential Equations and their Applications, Horwood, Chichester, 1997. [34] X. Mao and C. Yuan, Stochastic Differential Equations with Markovian Switching, Imperial College Press, 2006. [35] N. Macdonald, Time Lags in Biological Models. in: Lecture Notes in Biomathematics, Springer-Verlag, 1978. [36] W. Mao, L. Hu and X. Mao, Neutral stochastic functional differential equations with Lévy jumps under the local Lipschitz condition, Adv. Differ. Equ., 2017, 57, 1-24. [37] H. Qiu, M. Liu, K. Wang and Y. Wang, Dynamics of a stochastic predator-prey system with Beddington-DeAngelis functional response, Appl. Math. Comput., 2012, 219, 2303-2312. [38] H. Qiu and W. Deng, Optimal harvesting of a stochastic delay competitive Lotka-Volterra model with Lévy jumps, Appl. Math. Comput., 2018, 317, 210-222. [39] R. Rudnicki and K. Pichór, Influence of stochastic perturbation on prey-predator systems, Math Biosci., 2007, 206, 108-119. doi: 10.1016/j.mbs.2006.03.006 [40] F. Wei and C. Wang, Survival analysis of a single-species population model with fluctuations and migrations between patches, Appl. Math. Modelling, 2020, 81, 113-127. doi: 10.1016/j.apm.2019.12.023 [41] F. Wu and Y. Xu, Stochastic Lotka-Volterra population dynamics with infinite delay, SIAM J. Appl. Math., 2009, 70, 641-657. doi: 10.1137/080719194 [42] Z. Wang and M. Liu, Optimal impulsive harvesting strategy of a stochastic Gompertz model in periodic environments, Appl. Math. Lett., 2022, 125, 107733. doi: 10.1016/j.aml.2021.107733 [43] Z. Wang, M. Deng and M. Liu, Stationary distribution of a stochastic ratio-dependent predator-prey system with regime-switching, Chaos Solitons Fractals, 2021, 142, 110462. doi: 10.1016/j.chaos.2020.110462 [44] Y. Wang, F. Wu and X. Mao, Stability in distribution of stochastic functional differential equations, Syst. Control Lett., 2019, 132, 104513. doi: 10.1016/j.sysconle.2019.104513 [45] Y. Xu, F. Wu and Y. Tan, Stochastic Lotka-Volterra system with infinite delay, J. Comput. Appl. Math., 2009, 232, 472-480. doi: 10.1016/j.cam.2009.06.023 [46] C. Yuan, J. Zou and X. Mao, Stability in distribution of stochastic differential delay equations with markovian switching, Syst. Control Lett., 2003, 50, 195-207. doi: 10.1016/S0167-6911(03)00154-3 [47] C. Zhu and G. Yin, On hybrid competitive Lotka-Volterra ecosystems, Nonlinear Anal., 2009, 71, e1370-e1379. doi: 10.1016/j.na.2009.01.166 [48] W. Zuo, D. Jiang, X. Sun, T. Hayat and A. Alsaedi, Long-time behaviors of a stochastic cooperative Lotka-Volterra system with distributed delay, Physica A, 2018, 15, 542-559. [49] S. Zhang, S. Yuan and T. Zhang, A predator-prey model with different response functions to juvenile and adult prey in deterministic and stochastic environments, Appl. Math. Comput., 2022, 413, 126598. [50] X. Zhang and Q. Yang, Dynamical Behavior of a stochastic Predator-Prey model with general functional response and nonlinear jump-diffusion, Discrete Cont. Dyn-B, doi: 10.3934/dcdsb.2021177. [51] X. Zou, The protection and optimal harvesting problems for biological resource in random environment, China Doctor Dissertation Full-text Database, 2013. [52] W. Zuo and D. Jiang, Periodic solutions for a stochastic non-autonomous Holling-Tanner predator-prey system with impulses, Nonlinear Anal. Hybrid Syst., 2016, 22, 191-201. doi: 10.1016/j.nahs.2016.03.004 [53] W. Zuo and Y. Zhou, Density function and stationary distribution of a stochastic SIR model with distributed delay, Appl. Math. Lett., 2022, 129, 107931. doi: 10.1016/j.aml.2022.107931 -
-
Figures(2)
Export File
Citation
Chun Lu, Xiaohua Ding, Lei Zhang. STATIONARY DISTRIBUTION AND PERMANENCE OF A STOCHASTIC DELAY PREDATOR-PREY LOTKA-VOLTERRA MODEL WITH LÉVY JUMPS[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1328-1352. doi: 10.11948/20210077
Format
Content
DownLoad:
-
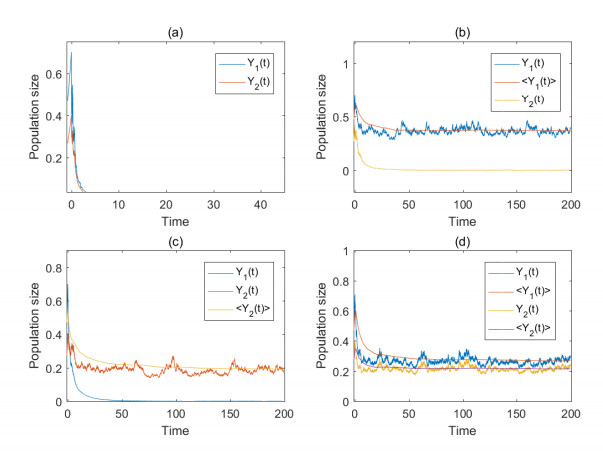
Figure 1. Step size
$ \Delta t=0.001 $ . The horizontal axis in this and following figures represent the time$ t $ . (a) is with$ L_{k}=0, \Xi_{1}(u)=-0.5 $ ; (b) is with$ L_{k}=0, \Xi_{1}(u)=-0.17 $ ; (c) is with$ L_{k}=e^{7}-1, \Xi_{1}(u)=-0.5 $ ; (d) is with$ L_{k}=e^{4}-1 $ ,$ \Xi_{1}(u)=-0.3 $ ,$ \Xi_{2}(u)=-0.3 $ -
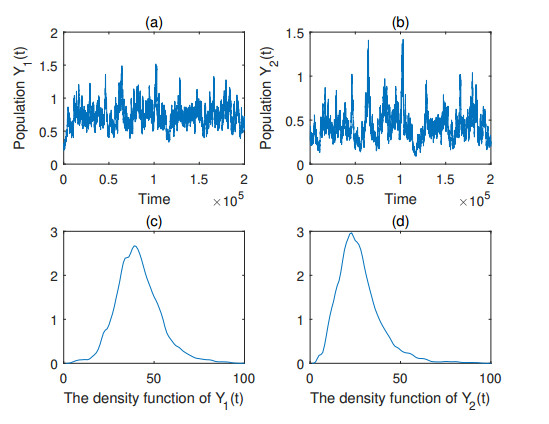
Figure 2. Step size
$ \Delta t=0.001 $ . (a) and (b) is a sample path of model (1.3); (c) is the probability density function of$ Y_{1}(t) $ at time$ t=1000 $ ; (d) is the probability density function of$ Y_{2}(t) $ at time$ t=1000 $