| Citation: |
Qiulan Zhao, Yadong Zhong, Xinyue Li. EXPLICIT SOLUTIONS TO A HIERARCHY OF DISCRETE COUPLING KORTEWEG-DE VRIES EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1353-1370. doi: 10.11948/20210081
|
EXPLICIT SOLUTIONS TO A HIERARCHY OF DISCRETE COUPLING KORTEWEG-DE VRIES EQUATIONS
-
Abstract
To get a hierarchy of discrete coupling Korteweg-de Vries equations, we consider from a discrete four-by-four matrix spectral problem. Then we can get the Lax pair of the KdV equations. Finally we present the explicit solutions of the KdV equations by constructing theirs Darboux transformations with the help of the corresponding Lax pairs.
-
Keywords:
- KdV equation /
- Darboux transformation /
- explicit solutions
-
-
References
[1] M. J. Ablowitz and H. Segur, Solitons and the Inverse Scattering Transform, SIAM, Philadelphia, 1981. [2] E. Cerpa, E. Crepeau and C. Moreno, On the boundary controllability of the Korteweg-de Vries equation on a star-shaped network, IMA J. Math. Control I., 2019, 1-15. [3] E. Fan and H. Zhang, New exact solutions to a system of coupled KdV equations, Phys. Lett. A, 1998, 245(5), 389-392. doi: 10.1016/S0375-9601(98)00464-2 [4] C. Gu, Soliton Theory and Its Application, Zhejiang Science and Technology Press, Zhejiang, 1990. [5] R. Hirota, Nonlinear Partial Difference Equations. I. A Difference Analogue of the Korteweg-de Vries Equation, J. Phys. Soc. Jap., 1977, 43(4), 1424-1433. doi: 10.1143/JPSJ.43.1424 [6] J. Ji and Z. Zhu, On a nonlocal modied Korteweg-de Vries equation: Integrability, Darboux transformation and soliton solutions, Commun. Nonlinear Sci., 2017, 42, 699-708. doi: 10.1016/j.cnsns.2016.06.015 [7] D. J. Korteweg and de Vries, On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves, Philos. Mag., 1895, 5(39), 422-443. [8] V. S. Kumar, H. Rezazadeh, M. Eslami, F. Izadi and M. S. Osman, Jacobi Elliptic Function Expansion Method for Solving KdV Equation with Conformable Derivative and Dual-Power Law Nonlinearity, Int. J. Appl. Comput. Math., 2019, 5, 127. doi: 10.1007/s40819-019-0710-3 [9] B. A. Kupershmidt, A super Korteweg-de Vries equation: An integrable system, Phys. Lett. A, 1984, 102(5-6), 213-215. doi: 10.1016/0375-9601(84)90693-5 [10] X. Li, Q. Zhao and Q. Yang, Integrable asymmetric AKNS model with multi-component, Commun. Nonlinear Sci. Numer. Simulat., 2020, 91, 105434. doi: 10.1016/j.cnsns.2020.105434 [11] L. Liu, X. Wen and D. Wang, A new lattice hierarchy: Hamiltonian structures, symplectic map and N-fold Darboux transformation, Appl. Math. Model., 2019, 67, 201-218. doi: 10.1016/j.apm.2018.10.030 [12] L. Liu, X. Wen and D. Wang, A new lattice hierarchy: Hamiltonian structures, symplectic map and N -fold Darboux transformation, Appl. Math. Model., 2019, 67, 201-218. doi: 10.1016/j.apm.2018.10.030 [13] W. Ma, A generating scheme for conservation laws of discrete zero curvature equations and its application, Comput. Math. Appl., 2019, 78, 3422-3428. doi: 10.1016/j.camwa.2019.05.012 [14] W. Ma, N-soliton solutions and the Hirota conditions in (1+1)-dimensions, Int. J. Nonlin. Sci. Num., 2021. [15] W. Ma, N-soliton solutions and the Hirota conditions in (2+1)-dimensions, Opt. Quant. Electron., 2020, 52(12). [16] W. Ma, A Darboux transformation for the Volterra lattice equation, Anal. Math. Phys., 2019, 9(4), 1711-1718. doi: 10.1007/s13324-018-0267-z [17] W. Ma, N-soliton solution and the Hirota condition of a (2+1)-dimensional combined equation, Math. Comput. Simulat., 2021, 190, 270-279. doi: 10.1016/j.matcom.2021.05.020 [18] W. Ma, N-soliton solution of a combined pKP-BKP equation, J. Geom. Phys., 2021, 165, 104191. doi: 10.1016/j.geomphys.2021.104191 [19] W. Ma, X. Yong and X. Lv, Soliton solutions to the B-type Kadomtsev–Petviashvili equation under general dispersion relations, Wave Motion, 2021, 103, 102719. doi: 10.1016/j.wavemoti.2021.102719 [20] V. B. Matveev and M. A. Salle, Darboux Transformations and Solitons, Springer, Berlin, 1991. [21] R. M. Miura, Korteweg-de Vries Equation and Generalizations. I. A Remarkable Explicit Nonlinear Transformation, J. Math. Phys., 1968, 9(8), 1202-1204. doi: 10.1063/1.1664700 [22] P. J. Olver, Applications of Lie Groups to Differential Equations, Springer-Verlag, New York, 1993. [23] S. Shen, C. Li, Y. Jin and W. Ma, Completion of the Ablowitz-Kaup-Newell-Segur integrable coupling, J. Math. Phys., 2018, 59, 103503. doi: 10.1063/1.4990534 [24] T. Tsuchida and M. Wadati, The Coupled Modified Korteweg-de Vries Equations, J. Phys. Soc. Jap., 1998, 67(4), 1175-1187. doi: 10.1143/JPSJ.67.1175 [25] H. D. Wahlquist and F. B. Estabrook, Bäcklund transformation for solutions of the Korteweg-de Vries equation, Phys. Rev. Lett., 1973, 31(23), 1386-1390. doi: 10.1103/PhysRevLett.31.1386 [26] X. Wen and C. Yuan, Controllable rogue wave and mixed interaction solutions for the coupled Ablowitz-Ladik equations with branched dispersion, Appl. Math. Lett., 2022, 123, 107591. doi: 10.1016/j.aml.2021.107591 [27] M. Wang, Exact solutions for a compound KdV-Burgers equation, Phys. Lett. A, 1996, 213, 279-287. doi: 10.1016/0375-9601(96)00103-X [28] J. Wu, A new combined soliton solution of the modified Korteweg-de Vries equation, Pramana J. Phys., 2020, 94, 123. doi: 10.1007/s12043-020-01958-1 [29] X. Xu, A hierarchy of Liouville integrable discrete Hamiltonian equations, Phys. Lett. A, 2008, 372, 3683-3693. doi: 10.1016/j.physleta.2008.02.047 [30] C. Yuan and X. Wen, Integrability, discrete kink multi-soliton solutions on an inclined plane background and dynamics in the modifed exponential Toda lattice equation, Nonlinear Dyn., 2021, 105, 643-669. doi: 10.1007/s11071-021-06592-z [31] Y. Zhang, W. Ma and O. Unsal, A novel kind of AKNS integrable couplings and their Hamiltonian structures, Turk. J. Math., 2017, 41, 1467-1476. doi: 10.3906/mat-1511-123 -
-
Figures(3)
Export File
Citation
Qiulan Zhao, Yadong Zhong, Xinyue Li. EXPLICIT SOLUTIONS TO A HIERARCHY OF DISCRETE COUPLING KORTEWEG-DE VRIES EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1353-1370. doi: 10.11948/20210081
Format
Content
DownLoad:
-
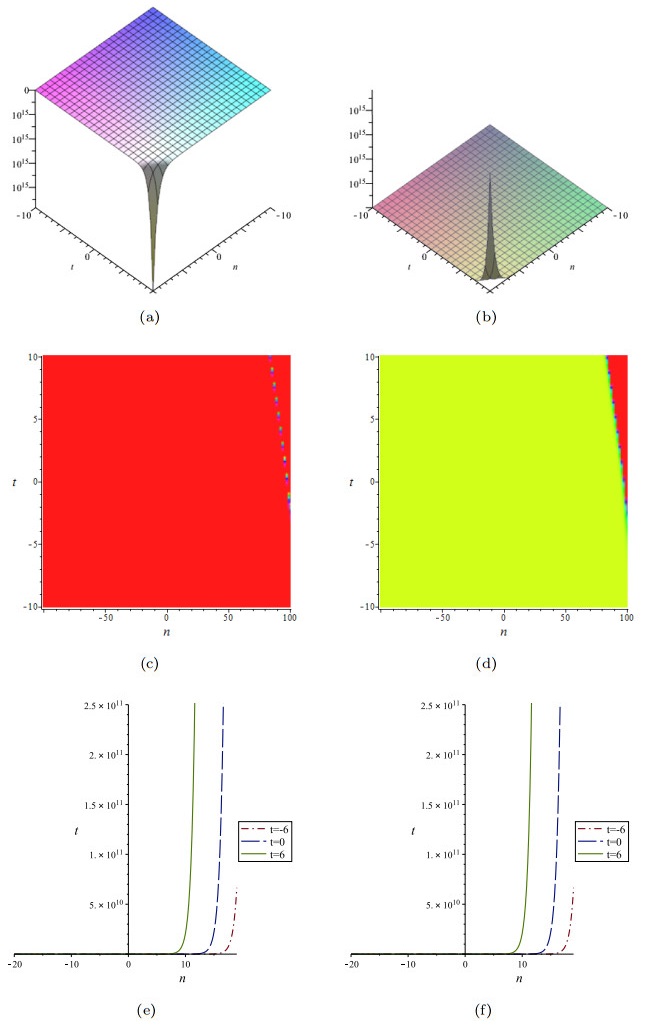
Figure 1. Solutions (51) with parameters
$ \lambda_{1}=0.5 $ ,$ \lambda_{2}=1 $ ,$ \kappa_{1}=-1 $ ,$ \kappa_{2}=1 $ . Figs. (a)-(c) and (e) the component$ \widetilde{u}_{n} $ , Figs. (b), (d) and (f) the component$ \widetilde{v}_{n} $ . -
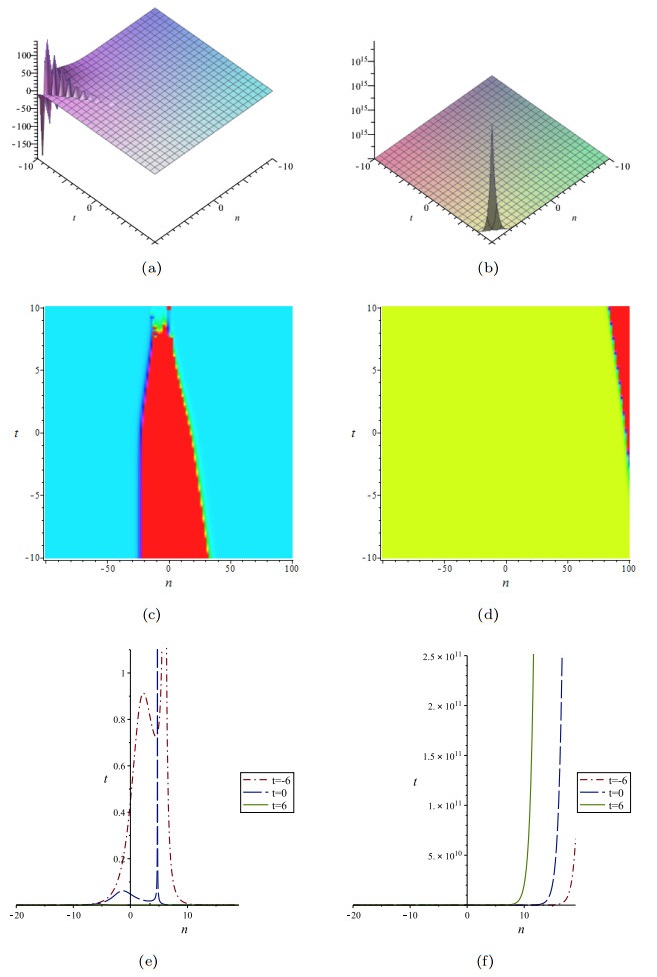
Figure 2. Solutions (55) with parameters
$ \lambda_{1}=1 $ ,$ \lambda_{2}=2 $ ,$ \kappa_{1}=-1 $ ,$ \kappa_{2}=1 $ . Figs. (a), (c) and (e) the component$ \widetilde{u}_{n} $ , Figs. (b), (d) and (f) the component$ \widetilde{v}_{n} $ . -
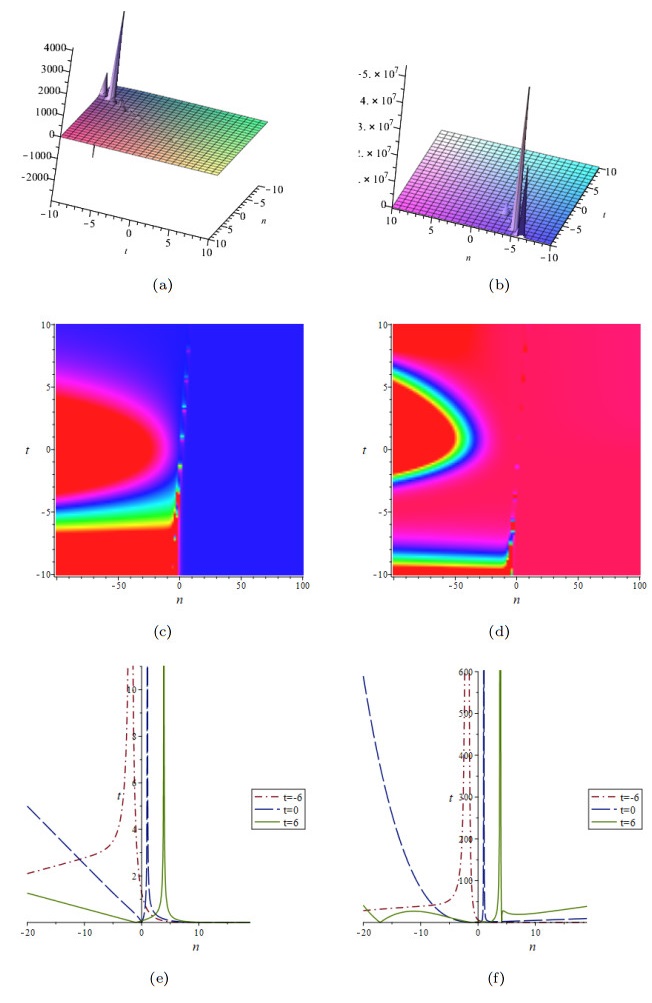
Figure 3. Solutions (59) with parameters
$ \lambda_{1}=1 $ ,$ \lambda_{2}=2 $ ,$ \kappa_{1}=-1 $ ,$ \kappa_{2}=1 $ . Figs. (a), (c) and (e) the component$ \widetilde{u}_{n} $ , Figs. (b), (d) and (f) the component$ \widetilde{v}_{n} $ .