| Citation: |
Ning Wei, Mei Li. STOCHASTICALLY PERMANENT ANALYSIS OF A NON-AUTONOMOUS HOLLING Ⅱ PREDATOR-PREY MODEL WITH A COMPLEX TYPE OF NOISES[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 479-496. doi: 10.11948/20210095
|
STOCHASTICALLY PERMANENT ANALYSIS OF A NON-AUTONOMOUS HOLLING Ⅱ PREDATOR-PREY MODEL WITH A COMPLEX TYPE OF NOISES
-
Abstract
This paper is considered a non-autonomous stochastic Holling Ⅱ predator-prey model with a complex type of noises. By constructing a Lyapunov function and applying the dominated convergence theorem, stochastically permanent is proved. More importantly, two values $\lambda_{1}$, $\lambda_{2}$ are expressed by using the density function of the Falk Planck equation and some parameters in the system. Among them, $\lambda_{1}>0$ is proved to be the sufficient condition for the persistence in mean. Then, applying the strong law of large number and exponential martingale inequality, two necessary lemmas are introduced. Furthermore, utilizing the lemmas and $\lambda_{2}<0$, the sufficient conditions for extinction of the system are obtained. Actually, the two sufficiency conditions obtained are approached to the necessary conditions. Finally, some numerical simulations are carried out to verify the influence of the complex type of noises on the system.
-
-
References
[1] C. Arancibia-Ibarraa and J. Floresc, Dynamics of a Leslie-Gower predator-prey model with Holling type II functional response, Allee effect and a generalist predator, Mathematics and Computers in Simulation, 2021, 188, 1–22. doi: 10.1016/j.matcom.2021.03.035 [2] D. Amartya and G. P. Samanta, Stochastic prey-predator model with additional food for predator, Physica A: Statistical Mechanics and its Applications, 2018, 512, 121-141. doi: 10.1016/j.physa.2018.08.138 [3] A. Bewyyman, The origin and evolution of predator-prey theory, Ecology, 1992, 73(5), 1530-1535. doi: 10.2307/1940005 [4] J. Bao and J. Shao, Permanence and extinction of regime-switching predator-prey models, SIAM Journal on Mathematical Analysis, 2015, 48(1), 725-739. [5] R. S. Cantrell and C. Cosner, On the dynamics of predator-prey models with the Beddington-DeAngelis functional response, Journal of Mathematical Analysis and Applications, 2001, 257(1), 206-222. doi: 10.1006/jmaa.2000.7343 [6] L. Chen and J. Chen, Nonlinear Biological Dynamical System, Science Press, Beijing, 1993. [7] B. Du, Existence, extinction and global asymptotical stability of a stochastic predator-prey model with mutual interference, Journal of Applied Mathematics and Computing, 2014, 46(1-2), 79-91. doi: 10.1007/s12190-013-0738-1 [8] N. Du and N. N. Nhu, Permanence and extinction of certain stochastic SIR models perturbed by a complex type of noises, Applied Mathematics Letters, 2017, 64(1), 223-230. [9] N. Du, D. H. Nguyen and G. Yin, Conditions for permanence and ergodicity of certain stochastic predator-prey models, Journal of Applied Probability, 2016, 53(1), 187-202. doi: 10.1017/jpr.2015.18 [10] S. Fu and H. Zhang, Effect of hunting cooperation on the dynamic behavior for a diffusive Holling type II predator-prey model, Communications in Nonlinear Science and Numerical Simulation, 2021. DOI: 10.1016/j.cnsns.2021.105807. [11] X. Guo, C. Zhu and D. Ruan, Dynamic behaviors of a predator-prey model perturbed by a complex type of noises, Physica A: Statistical Mechanics and its Applications, 2019, 523, 1024-1037. doi: 10.1016/j.physa.2019.04.104 [12] C. S. Holling, The functional response of predator to prey density and its role in mimicry and population regulation, Memoirs of the Entomological Society of Canada, 1959, 91(45), 385-398. [13] Y. Hu, F. Wu and C. Huang, Stochastic Lotka–Volterra models with multiple delays, Journal of Mathematical Analysis and Applications, 2011, 375(1), 42-57. doi: 10.1016/j.jmaa.2010.08.017 [14] D. J. Higham, An algorithmic introduction to numerical simulation of stochastic differential equations, SIAM Review, 2001, 43(3), 525-546. doi: 10.1137/S0036144500378302 [15] C. Ji and D. Jiang, Persistence and non-persistence of a mutualism system with stochastic perturbation, Discrete and Continuous Dynamical Systems, 2013, 32(3), 867-889. [16] C. Ji, D. Jiang and D. Lei, Dynamical behavior of a one predator and two independent preys system with stochastic perturbations, Physica A: Statistical Mechanics and its Applications, 2019, 515(1), 649-664. [17] R. Z. Khas'minskii, Ergodic properties of recurrent diffusion processes and stabilization of the Cauchy problem for parabolic equations, Theory of Probability and its Applications, 1960, 5(2), 179-196. doi: 10.1137/1105016 [18] R. Z. Khas'minskii, Stochastic stability of differential equations, Springer-Verlag, Berlin Heidelberg, 2012. [19] Y. Li and Y. Ye, Multiple positive almost periodic solutions to an impulsive non-autonomous Lotka-Volterra predator-prey system with harvesting terms, Communications in Nonlinear Science and Numerical Simulation, 2013, 18(11), 3190-3201. doi: 10.1016/j.cnsns.2013.03.014 [20] Q. Liu, L. Zu and D. Jiang, Dynamics of stochastic predator-prey models with Holling II functional response, Communications in Nonlinear Science and Numerical Simulation, 2016, 37, 62-76. doi: 10.1016/j.cnsns.2016.01.005 [21] Z. Lu and Y. Takeuchi, Permanence and global stability of cooperative Lotka-Volterra diffusion systems, Nonlinear Analysis, 1992, 19(10), 963-975. doi: 10.1016/0362-546X(92)90107-P [22] M. Liu and P. S. Mandal, Dynamical behavior of a one-prey two-predator model with random perturbations, Communications in Nonlinear Science and Numerical Simulation, 2015, 28(1-3), 123-137. doi: 10.1016/j.cnsns.2015.04.010 [23] M. Li, H. Gao, C. Sun and Y. Gong, Analysis of a mutualism model with stochastic perturbations, International Journal of Biomathematics, 2015. DOI: 10.1142/S1793524515500722. [24] J. Lv and K. Wang, Asymptotic properties of a stochastic predator-prey system with Holling II functional response, Communications in Nonlinear Science and Numerical Simulation, 2011, 16(10), 4037-4048. doi: 10.1016/j.cnsns.2011.01.015 [25] M, Li, H. Gao and B. Wang, Analysis of a non-autonomous mutualism model driven by Lévy jumps, Discrete and Continuous Dynamical Systems-Series B, 2017, 21(4), 1189-1202. [26] X. Li, A. Gay, D. Jiang and X. Mao, Sufficient and necessary conditions of stochastic permenace and extinction for stochastic logistic populations under regime switching, Journal of Mathematical Analysis and Applications, 2011, 376(1), 11-28. doi: 10.1016/j.jmaa.2010.10.053 [27] X. Li, J. Da and X. Mao, Population dynamical behavior of Lotka–Volterra system under regime swiching, Journal of Computational and Applied Mathematics, 2009, 232(2), 427-448. doi: 10.1016/j.cam.2009.06.021 [28] X. Mao, G. Marion and E. Renshaw, Environmental brownian noise suppresses explosions in populations dynamics, Stochastic Processes and their Applications, 2002, 97(1), 95-110. doi: 10.1016/S0304-4149(01)00126-0 [29] X. Mao, Stochastic Differential Equations and Applications, Horwood Publishing Limited, Chichester, 2007. [30] X. Mao, Stationary distribution of stochasti c population systems, Systems and Control Letters, 2011, 60(6), 398-405. doi: 10.1016/j.sysconle.2011.02.013 [31] K. Nosrati and M. Shafiee, Dynamic analysis of fractional-order singular Holling type-II predator-prey system, Applied Mathematics and Computation, 2017, 313, 159-179. doi: 10.1016/j.amc.2017.05.067 [32] S. P. Rajasekar, M. Pitchaimani and Q. Zhu, Progressive dynamics of a stochastic epidemic model with logistic growth and saturated treatment, Physica A: Statistical Mechanics and its Applications, 2019. DOI: 10.1016/j.physa.2019.122649. [33] R. Rudnicki and K. Pichór, Influence of stochastic perturbation on prey–predator systems, Mathematical Biosciences, 2007, 206(1), 108-119. doi: 10.1016/j.mbs.2006.03.006 [34] Y. Wang and H. Wu, Global dynamics of Lotka-Volterra equations characterizing multiple predators competing for one prey, Journal of Mathematical Analysis and Applications, 2020. DOI: 10.1016/j.jmaa.2020.124293. [35] J. Wang and M. Wang, The diffusive Beddington-DeAngelis predator-prey model with nonlinear prey-taxis and free boundary, Mathematical Methods in the Applied Sciences, 2018, 41(16), 6741-6762. doi: 10.1002/mma.5189 [36] W. Yang, Extinction and permanence of a diffusive predator-prey model with modified leslie-gower functional response, Journal of Mathematics, 2017, 37(3), 627-636. [37] G. Yin and C. Zhu, Hybrid switching diffusions: properties and applications, In: Stochastic Modeling and Applied Probability, Springer, New York, 2010. [38] Y. Zhang, Asymptotic behavior of non-autonomous stochastic Gilpin-Ayala predator-prey model with jumps, The Journal of Nonlinear Sciences and Applications, 2017, 10, 2079-2093. doi: 10.22436/jnsa.010.04.62 -
-
Figures(3)
Export File
Citation
Ning Wei, Mei Li. STOCHASTICALLY PERMANENT ANALYSIS OF A NON-AUTONOMOUS HOLLING Ⅱ PREDATOR-PREY MODEL WITH A COMPLEX TYPE OF NOISES[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 479-496. doi: 10.11948/20210095
Format
Content
DownLoad:
-
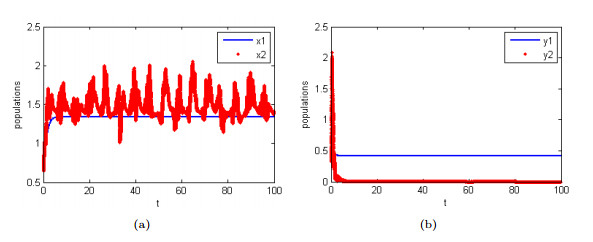
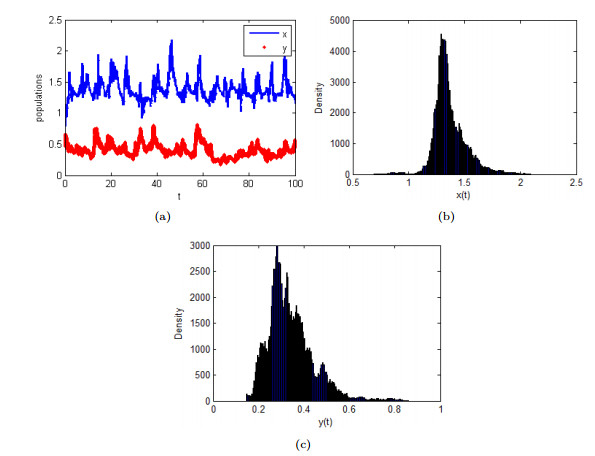
Figure 1. (a) reflects the change in the population of
$ x(t) $ and$ y(t) $ of system (1.3) under a small stochastic disturbance. (b), (c) is the frequency histograms of$ x(t) $ and$ y(t) $ . -
Figure 2. (a)
$ x_{1}(t) $ represent the prey of the system (1.1) without stochastic disturbance, and$ x_{2}(t) $ is the prey of system (1.3). (b) The representation of$ y_{1}(t) $ and$ y_{2}(t) $ are corresponded to$ x_{1}(t) $ and$ x_{2}(t) $ . -
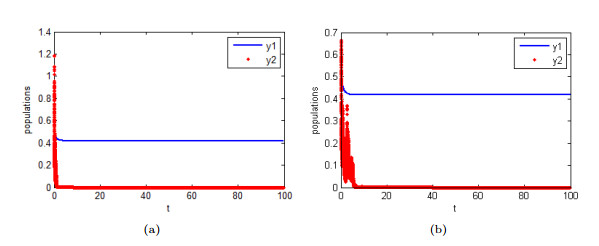
Figure 3. Changes in the number of populations in two cases.
$ y_{1}(t) $ and$ y_{2}(t) $ have the same representation as Figure 2. (a)$ \sigma_{2}(t) = 3+0.1\cos(t) $ ,$ \sigma_{4}(t) = 0.1+0.1\cos(t) $ . (b)$ \sigma_{2}(t) = 0.2+0.1\cos(t) $ ,$ \sigma_{4}(t) = 3+0.1\cos(t) $ .