| Citation: | Shazia Sadiq, Mujeeb ur Rehman. ψ-SHIFTED OPERATIONAL MATRIX SCHEME FOR FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 497-516. doi: 10.11948/20210101 |
ψ-SHIFTED OPERATIONAL MATRIX SCHEME FOR FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS
-
Abstract
In this paper, we present a numerical method to solve space-time fractional partial differential equations. We introduce $ \psi$-shifted Chebyshev polynomials to construct operational matrices of fractional differentiation in the Caputo sense. These operational matrices are then used to find the solution of fractional partial differential equations. The efficiency and applicability of introduced numerical scheme is tested by comparing the proposed numerical approximations with the results obtained from existing numerical methods.
-

-
References
[1] R. Almeida, A Caputo fractional derivative of a function with respect to another function, Commun. Nonlinear Sci. Numer. Simul., 2017, 44(2017), 460-481. [2] R. Almeida, Functional differential equations involving the $ \psi$-Caputo fractional derivative, Fractal Fract., 2020, 4(2), 29. doi: 10.3390/fractalfract4020029 CrossRef $ \psi$-Caputo fractional derivative" target="_blank">Google Scholar
[3] R. Almeida, M. Jleli and B. Samet, A numerical study of fractional relaxation oscillation equations involving $ \psi$-Caputo fractional derivative, Rev. R. Acad. Cienc. Exactas, Fís. Nat. Ser. Madr., 2019, 113(3), 1873-1891. doi: 10.1007/s13398-018-0590-0 CrossRef $ \psi$-Caputo fractional derivative" target="_blank">Google Scholar
[4] M. Awadalla and Y. Y. Yameni, Modeling exponential growth and exponential decay real phenomena by $ \psi$-Caputo fractional derivative, J. Adv. Math. Comput. Sci., 2018, 1-13. $ \psi$-Caputo fractional derivative" target="_blank">Google Scholar
[5] Z. Baitiche, C. Derbazi, J. Alzabut, M. E. Samei, M. K. Kaabar and Z. Siri, Monotone iterative method for $ \psi$-Caputo fractional differential equation with nonlinear boundary conditions, Fractal Fract., 2021, 5(3), 81. doi: 10.3390/fractalfract5030081 CrossRef $ \psi$-Caputo fractional differential equation with nonlinear boundary conditions" target="_blank">Google Scholar
[6] H. Dehestani, Y. Ordokhani and M. Razzaghi, Application of the modified operational matrices in multiterm variable-order time-fractional partial differential equations, Math. Meth. Appl. Sci., 2019, 42(18), 7296-7313. doi: 10.1002/mma.5840 [7] T. Dinu, Interpolation of the Functions with Two Variable Values with Simple Nodes, Bul. Univ. Petrol-Gaze Ploiesti., 2007, LIX(1), 7-12. [8] Q. H. Do, H. T. Ngo and M. Razzaghi, A generalized fractional-order Chebyshev wavelet method for two-dimensional distributed-order fractional differential equations, Commun. Nonlinear Sci. Numer. Simul., 2021, 95, 105597. doi: 10.1016/j.cnsns.2020.105597 [9] M. El-Kady and A. El-Sayed, Fractional differentiation matrices for solving fractional orders differential equations, Int. J. Pure Appl. Math., 2013, 84 (2), 1-13. [10] A. M. A. El-Sayed and M. Gaber, The Adomian decomposition method for solving partial differential equations of fractal order in finite domains, Phys. Lett. A., 2006, 359(3), 175-182. doi: 10.1016/j.physleta.2006.06.024 [11] W. Gander, Change of basis in polynomial interpolation, Numer. Linear Algebra Appl., 2005, 12(8), 769-778. doi: 10.1002/nla.450 [12] H. Hassani, J. T. Machado, Z. Avazzadeh and E. Naraghirad, Generalized shifted Chebyshev polynomials: Solving a general class of nonlinear variable order fractional PDE, Commun. Nonlinear Sci. Numer. Simul., 2020, 85, 105229. doi: 10.1016/j.cnsns.2020.105229 [13] M. H. Heydari, Z. Avazzadeh and M. F. Haromi, A wavelet approach for solving multi-term variable-order time fractional diffusion-wave equation, Appl. Math. Comput., 2019, 341(2019), 215-228. [14] H. Jafari and S. Seifi, Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation, Commun. Nonlinear Sci. Numer. Simul., 2009, 14(5), 2006-2012. doi: 10.1016/j.cnsns.2008.05.008 [15] M. Javidi and B. Ahmad, Numerical solution of fractional partial differential equations by numerical Laplace inversion technique, Adv. Differ. Equ., 2013, 2013(1), 1-18. doi: 10.1186/1687-1847-2013-1 [16] A. Kadem, The fractional transport equation: an analytical solution and a spectral approximation by Chebyshev polynomials, Appl. Sci., 2009, 11, 78-90. [17] S. Kumar and C. Piret, Numerical solution of space-time fractional PDEs using RBF-QR and Chebyshev polynomials, Appl. Numer. Math., 2019, 143(2019), 300-315. [18] M. M. Matar, M. I. Abbas, J. Alzabut, M. K. A. Kaabar, S. Etemad and S. Rezapour, Investigation of the $ p$-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives, Adv. Differ. Equ., 2021, 2021(1), 1-18. doi: 10.1186/s13662-020-03162-2 CrossRef $ p$-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives" target="_blank">Google Scholar
[19] S. Mockary, E. Babolian and A. R. Vahidi, A fast numerical method for fractional partial differential equations, Adv. Differ. Equ., 2019, 2019(1). [20] S. Momani and Z. Odibat, A novel method for nonlinear fractional partial differential equations: Combination of DTM and generalized Taylor's formula, J. Comput. Appl. Math., 2008, 220(1-2), 85-95. doi: 10.1016/j.cam.2007.07.033 [21] S. Nemati and Y. Ordokhani, Legendre expansion methods for the numerical solution of nonlinear 2D Fredholm integral equations of the second kind, J. Appl. Math. Informatics, 2013, 31(5-6), 609-621. [22] D. Occorsio and W. Themistoclakis, Uniform weighted approximation on the square by polynomial interpolation at Chebyshev nodes, Appl. Math. Comput., 2020 385, 125457. [23] M. Rehman, D. Baleanu, J. Alzabut, M. Ismail and U. Saeed, Green-Haar wavelets method for generalized fractional differential equations, Adv. Differ. Equ., 2020, 2020(1), 1-25. doi: 10.1186/s13662-019-2438-0 [24] M. Rehman and R. A. Khan, Numerical solutions to initial and boundary value problems for linear fractional partial differential equations, Appl. Math. Model, 2013, 37(7), 5233-5244. doi: 10.1016/j.apm.2012.10.045 [25] H. Singh and C. S. Singh, Stable numerical solutions of fractional partial differential equations using Legendre scaling functions operational matrix, Ain Shams Eng. J., 2018, 9(4), 717-725. doi: 10.1016/j.asej.2016.03.013 [26] C. Thaiprayoon, W. Sudsutad, J. Alzabut, S. Etemad and S. Rezapour, On the qualitative analysis of the fractional boundary value problem describing thermostat control model via $\psi$-Hilfer fractional operator, Adv. Differ. Equ., 2021, 2021(1), 1-28. doi: 10.1186/s13662-020-03162-2 CrossRef $ \psi$-Hilfer fractional operator" target="_blank">Google Scholar
[27] H. Tu, Y. Wang, Q. Lan, W. Liu, W. Xiao and S. Ma, A Chebyshev-Tau spectral method for normal modes of underwater sound propagation with a layered marine environment, J. Sound and Vib., 2021, 492, 115784. doi: 10.1016/j.jsv.2020.115784 [28] D. Varsamis, P. Mastorocostas and N. Karampetakis, Transformations between two-variable polynomial bases with applications, Appl. Math. Inf. Sci., 2016, 10(4), 1303-1311. doi: 10.18576/amis/100409 [29] Z. Yang and H. Zhang, Chebyshev polynomials for approximation of solution of fractional partial differential equations with variable coefficients, IC3ME Atlantis Press, 2015. [30] M. Yi, J. Huang and J. Wei, Block pulse operational matrix method for solving fractional partial differential equation, Appl. Math. Comput., 2013, 221, 121-131. [31] F. Yin, J. Song, Y. Wu and L. Zhang, Numerical solution of the fractional partial differential equations by the two-dimensional fractional-order Legendre functions, Abstr. Appl. Anal., 2013, (2013). [32] Y. H. Youssri and R. M. Hafez, Chebyshev collocation treatment of Volterra-Fredholm integral equation with error analysis, Arab. J. Math., 2020, 9(2), 471-480. doi: 10.1007/s40065-019-0243-y -
-
-
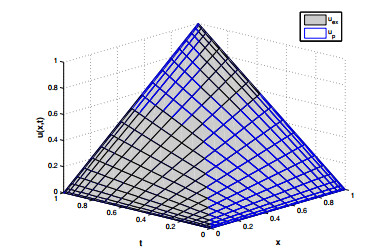
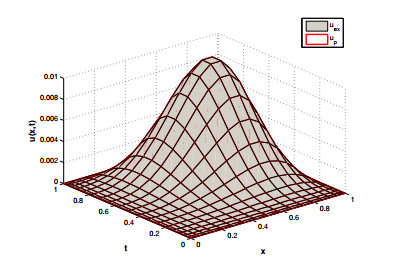
Figure 1. Exact and proposed solution for
$ \psi_1 $ at$ \alpha = \beta = 1.8 $ . -
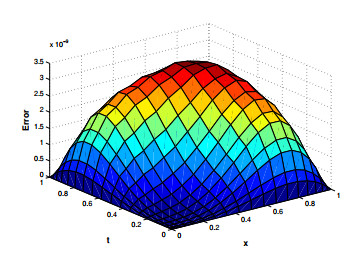
Figure 2. Error for
$ \psi_1 $ at$ \alpha = \beta = 1.8 $ . -
Figure 3. Exact and proposed solution for
$ \psi_1 $ at$ \alpha = \beta = 1.8 $ . -
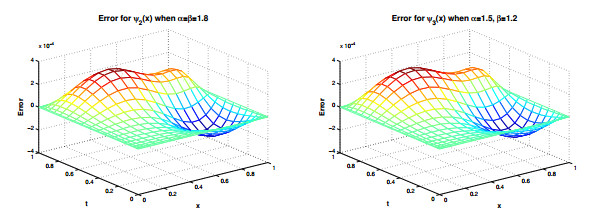
Figure 4. Error for different
$ \psi $ 's taking multiple values of$ \alpha $ and$ \beta $ . -
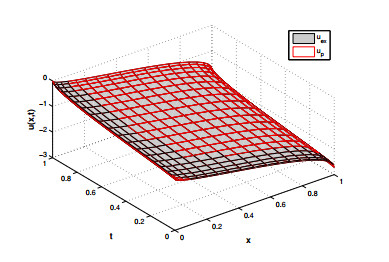
Figure 5. Exact and proposed solution at
$ \alpha = 1.5 $ -
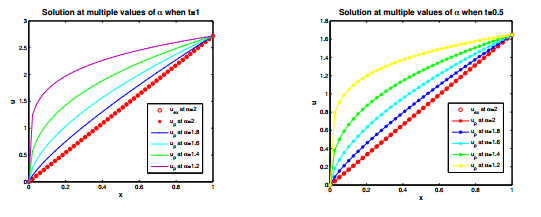
Figure 6. Exact and proposed solution for multiple values of
$ \alpha $ at$ t = 1 $ and$ t = 0.5. $ .




 DownLoad:
DownLoad: