| Citation: |
Jose Luis Diaz Palencia, Federico Prieto Munoz, Juan Miguel Garcia-Haro. NON-HOMOGENEOUS REACTION IN A NON-LINEAR DIFFUSION OPERATOR WITH ADVECTION TO MODEL A MASS TRANSFER PROCESS[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 179-205. doi: 10.11948/20210096
|
NON-HOMOGENEOUS REACTION IN A NON-LINEAR DIFFUSION OPERATOR WITH ADVECTION TO MODEL A MASS TRANSFER PROCESS
-
Abstract
It is the objective to provide a mathematical treatment of a non-homogeneous and non-lipschitz reaction problem with a non-linear diffusion and advection operator, so that it can be applied to a fire extinguishing process in aerospace. The main findings are related with the existence and characterization of a finite propagation support that emerges in virtue of the the non-linear diffusion formulation. It is provided a precise assessment on different times associated to the extinguisher discharge process. Particularly, the time required to activate the discharge, the time required for the extinguisher front to cover the whole domain, the time required to reach a minimum level of concentration so as to extinguish a fire and the time required by the agent to reach some difficult dead zones where the extinguisher propagates only by diffusion and no advection. The equation proposed is firstly discussed from a mathematical perspective to find analytical solutions and propagating profiles. Afterwards, the application exercise is introduced.
-
Keywords:
- Reaction, non-linear advection /
- non-linear diffusion /
- non-homogenous /
- aerospace
-
-
References
[1] P. Arturo and J. L. Vázquez, The balance between strong reaction and slow diffusion, Communications in Partial Differential Equations, 1990, 15, 159-183. doi: 10.1080/03605309908820682 [2] P. Arturo and J. L. Vázquez, Travelling Waves and Finite Propagation in a Reaction-Diffusion Equation, Journal of Differential Equations, 1991, 93, 19-61. doi: 10.1016/0022-0396(91)90021-Z [3] J. Bedrossian, N. Rodríguez and A. Bertozzi, Local and global wellposedness for aggregation equations and patlak–keller–segel models with degenerate diffusion, Nonlinearity, 2001, 24(6), 1683. [4] J. M. Bennett, Principles, Testing and in-field experience for the fire panel fuel tank protection device, SAE, 2005. [5] A. Bertozzi and D. Slepcev, Existence and uniqueness of solutions to an aggregation equation with degenerate diffusion, Communications on Pure and Applied Analysis, 2009, 9(6), 1617. [6] M. Bertsch and D. Hilhorst, A density dependent diffusion equation in population dynamics: stabilization to equilibrium, SIAM Journal on Mathematical Analysis, 1986, 17(4), 863-883. doi: 10.1137/0517062 [7] M. Bhatti, A. Zeeshan, R. Ellahi, O. Anwar Bég and A. Kadir, Effects of coagulation on the two-phase peristaltic pumping of magnetized prandtl biofluid through an endoscopic annular geometry containing a porous medium, Chin. J. Phys. 2019, 58, 222-23. https://doi.org/10.1016/j.cjph.2019.02.004. doi: 10.1016/j.cjph.2019.02.004 [8] D. Blake and J. Suo-Anttila, Aircraft cargo compartment fire detection and smoke transport modeling, Fire Safety Journal, 2008, 43(8), 576-582. doi: 10.1016/j.firesaf.2008.01.003 [9] A. De Pablo, Doctoral Thesis. Estudio de una ecuación de reacción-difusión, Universidad Autónoma de Madrid, 1989. [10] J. Díaz, Modeling of an aircraft fire extinguishing process with a porous medium equation. SN Appl. Sci, 2020, 2, 2108. https://doi.org/10.1007/s42452-020-03891-9. doi: 10.1007/s42452-020-03891-9 [11] L. Evans, Partial Differential Equations, Advanced Mathematical Society, United States of America, 2010. [12] R. Ferreira, A. De Pablo, G. Reyes and A. Sánchez, The interfaces of an inhomogeneous Porous Medium Equation with Convection, Comm. in Partial Diff. Eq., 2006, 31, 497-514. doi: 10.1080/03605300500481343 [13] E. R. Galea and N. C. Markatos, A review of mathematical modelling of aircraft cabin fires, Applied Mathematical Modelling, 1987, 11(3), 162-176. doi: 10.1016/0307-904X(87)90001-1 [14] B. Gilding, Improved theory for a nonlinear degenerate parabolic equation, Ann. Scu. Norm. Sup. Pisa, 1989, 16, 165-224. [15] P. Grasso, S. Mauro and A. Innocente, Two-dimensional reaction-advection-diffusion model of the spread of fire in wildlands, Book Chapter published in Advances in forest fire research, 2018, 334-342. [16] R. Harish and K. Venkatasubbaiah, Mathematical modeling and computation of fire induced turbulent flow in partial enclosures, Applied Mathematical Modelling, 2013, 37(23), 9732-9746. doi: 10.1016/j.apm.2013.05.011 [17] S. A. Hosseini, N. Darabiha and D. Thévenin, Lattice Boltzmann advection-diffusion model for conjugate heat transfer in heterogeneous media, International Journal of Heat and Mass Transfer, 2019, 132, 906-919. doi: 10.1016/j.ijheatmasstransfer.2018.12.034 [18] S. Kamin and P. Rosenau, Propagation of thermal waves in an inhomogeneous medium, Comm. Pure and Applied Math, 1989, 34, 831-852. [19] R. Kersner, G. Reyes and A. Tesei, On a class of parabolic equations with variable density and absorption, Adv. Diff. Equations, 2002, 7, 155-176. [20] J. Kim, B. Baek and J. Lee, Numerical analysis of flow characteristics of fire extinguishing agents in aircraft fire extinguishing systems, J. Mech. Sci Technol., 2009, 23, 1877-1884. doi: 10.1007/s12206-009-0618-7 [21] H. Li, Hopf Bifurcation of Delayed Density-Dependent Predator-Prey Model, Acta. Math. Sci, 2019, 39(2), 358-371. [22] A. Maranguides, R. Sheinson, R. Darwin, D. Kay and D. Barylski, Halon 1301 Retrofit Implementation Considerations, Naval Researh Laboratory, Combustion Dynamics Section. [23] S. Nazari, R. Ellahi, M. M. Sarafraz et al., Numerical study on mixed convection of a non-Newtonian nanofluid with porous media in a two lid-driven square cavity, J. Therm Anal Calorim, 2020, 140, 1121-1145. https://doi.org/10.1007/s10973-019-08841-1. doi: 10.1007/s10973-019-08841-1 [24] C. Pao, Nonlinear Parabolic and Elliptic Equations, Springer Science+Bussiness Media, North Carolina, United States of America, 2012. [25] T. A. Penteado, Analysis of fire extinguishing agent concentration in commercial aircraft cargo compartment, Master dissertation, Technological Institute of Aeronautics, 2004, 111. [26] J. Santrock and S. E. Hodges, Evaluation of automatic fire suppression system in full scale vehicle fire tests and static vehicle fire test, SAE, 2004. [27] A. Shahid, H. Huang, M. M. Bhatti, L. Zhang and R. Ellahi, Numerical Investigation on the Swimming of Gyrotactic Microorganisms in Nanofluids through Porous Medium over a Stretched Surface, Mathematics, 2020, 8, 380. https://doi.org/10.3390/math803038. doi: 10.3390/math803038 [28] J. L. Vázquez, The Porous Medium Equation, mathematical theory, Oxford Mathematical Monographs, Oxford, 2006. [29] Y. Zhang, Degenerate Diffusions with Advection, Doctoral Thesis, University of California, 2019. [30] Y. Zhou, Exact Solutions and dynamics of the Raman Soliton model in Nanoscale Optical Waveguides, with metamaterials, having parabolic law non-linearity, Journal of Applied Analysis & Computation, 2019, 9(1), 159-186. doi: 10.11948/2019.159. -
-
Figures(6) / Tables(1)
Export File
Citation
Jose Luis Diaz Palencia, Federico Prieto Munoz, Juan Miguel Garcia-Haro. NON-HOMOGENEOUS REACTION IN A NON-LINEAR DIFFUSION OPERATOR WITH ADVECTION TO MODEL A MASS TRANSFER PROCESS[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 179-205. doi: 10.11948/20210096
Format
Content
DownLoad:
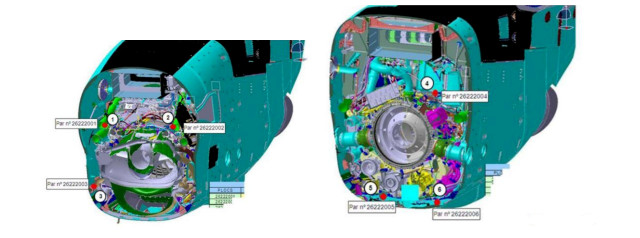
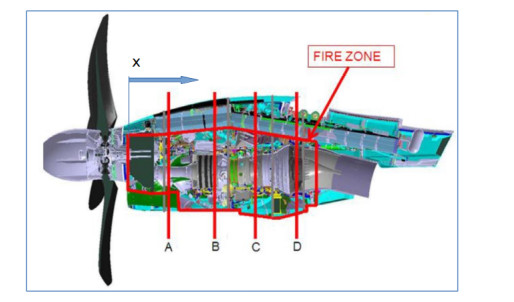
- Figure 1. Domain representation. Note that the sensors are placed close to each of the sections A, B, C and D
- Figure 2. Extinguisher sensor position and numbering for Section A (left) and Section B (right).
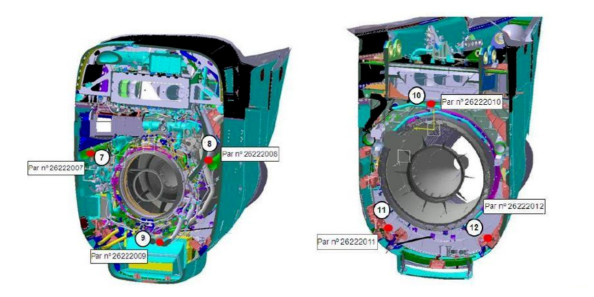
- Figure 3. Extinguisher sensor position and numbering for Section C (left) and Section D (right).
-
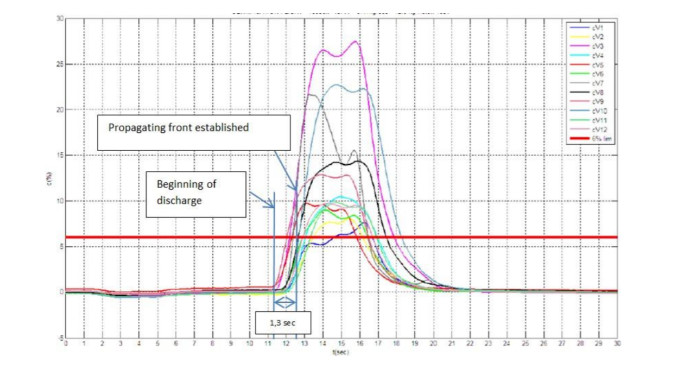
Figure 4. Extinguisher volumetric concentration evolution upon fire activation procedure that is initiated during the flight test used to validate the postulated diffusion. Each of the coloured lines represent the measurements of a sensor located as described in the previous figures. Note that the horizontal red bar represents a volumetric concentration of
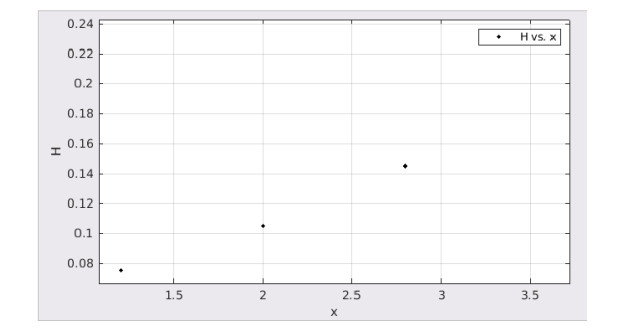
$ 6\% $ . At$ 1.3 $ seconds from the beginning of discharge, half of the sensors reach the$ 6\% $ level. - Figure 5. fire suppressant concentration (H) represented versus the axial variable x (meters)
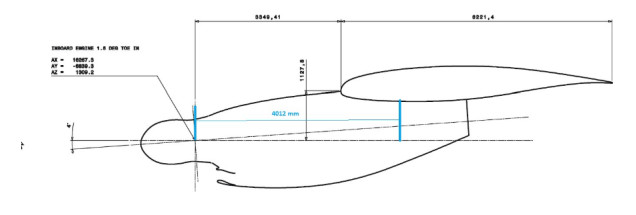
- Figure 6. Nacelle shape geometry