| Citation: | Qian Yang, Mingkang Ni. ASYMPTOTICS OF THE SOLUTION TO A PIECEWISE-SMOOTH QUASILINEAR SECOND-ORDER DIFFERENTIAL EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 256-269. doi: 10.11948/20210147 |
ASYMPTOTICS OF THE SOLUTION TO A PIECEWISE-SMOOTH QUASILINEAR SECOND-ORDER DIFFERENTIAL EQUATION
-
Abstract
We investigate a singularly perturbed boundary value problem for a piecewise-smooth second-order quasilinear differential equation in the case when the discontinuous curve which separates the domain is monotone. Applying the boundary layer function method, the asymptotic expansion of a solution with internal layer appearing in the neighborhoods of some point on the monotone curve and the point itself is constructed. For sufficiently small parameter values, using the matching method, the existence of a smooth solution with an internal transition layer in the neighborhood of a point of the monotone curve is proved. A simple example is given to show the effectiveness of our method.
-

-
References
[1] V. F. Butuzov, N. N. Nefedov and K. R. Schneider, Singularly perturbed elliptic problems in case of exchange of stability, Journal of Differential Equations, 2001, 169, 373-395. doi: 10.1006/jdeq.2000.3904 [2] V. F. Butuzov, A. B. Vasil'eva and N. N. Nefedov, Asymptotic theory of contrasting structures, Automation and Remote Control, 1997, 58(7), 1068-1091. [3] C. A. Buzzi, P. R. da Silva and M. A. Teixeira, Slow-fast systems on algebraic varieties bordering piecewise-smooth dynamical systems, Bulletin Des Sciences Mathematiques, 2012, 136, 444-462. doi: 10.1016/j.bulsci.2011.06.001 [4] H. Chen, Social status human capital formation and super-neutrality in a two sector monetary economy, Economic Modeling, 2011, 28, 785-794. doi: 10.1016/j.econmod.2010.10.010 [5] Z. Du, J. Li and X. Li, The existence of solitary wave solutions of delayed Camassa-Holm equation via a geometric approach, Journal of Functional Analysis, 2018, 275, 988-1007. doi: 10.1016/j.jfa.2018.05.005 [6] A. F. Filippov, Differential equations with discontinuous righthand sides, Springer, 1988. [7] G. Fusco and N. Guglielmi, A regularization for discontinuous differential equations with application to state-dependent delay differential equations of neutral type, Journal of Differential Equations, 2011, 250, 3230-3279. doi: 10.1016/j.jde.2010.12.013 [8] Z. Guo and L. Huang, Global exponential convergence and global convergence in finite time of non-autonomous discontinuous neural networks, Nonlinear Dynamics, 2009, 58, 349-359. doi: 10.1007/s11071-009-9483-2 [9] Z. Guo and L. Huang, LMI conditions for global robust stability of delayed neural networks with discontinuous neuron activations, Applied Mathematics and Computation, 2009, 215(3), 889-900. doi: 10.1016/j.amc.2009.06.013 [10] Z. Guo, L. Huang, and X. Zou, Impact of discontinuous treatments on disease dynamics in an SIR epidemic model, Mathematical Biosciences and Engineering, 2012, 9(1), 97-110. doi: 10.3934/mbe.2012.9.97 [11] J. W. Hargrove, J. H. Humphrey, A. Mahomva, et al, Declining HIV prevalence and incidence in perinatal women in Harare, Zimbabwe Epidemics, 2011, 3, 88-94. doi: 10.1016/j.epidem.2011.02.004 [12] E. M. D. Jager and F. Jiang, The Theory of Singular Perturbations, Elsevier, North Holland, 1996. [13] F. Jiang and M. Han, Qualitative analysis of crossing limit cycles in discontinuous Liénard-type differential systems, Journal of Nonlinear Modeling and Analysis, 2019, 1(4), 527-543. [14] N. Levashova, A. Melnikova, A. Semina and A. Sidorova, Autowave mechanisms of structure formation in urban ecosystems as the process of self-organization in active media, Communication on Applied Mathematics and Computation, 2017, 31(1), 32-42. [15] N. T. Levashova, N. N. Nefedov and A. O. Orlov, Time-independent reaction-diffusion equation with a discontinuous reactive term, Computational Mathematics and Mathematical Physics, 2017, 57(5), 854-866. doi: 10.1134/S0965542517050062 [16] N. T. Levashova, N. N. Nefedov and A. O. Orlov, Asymptotic stability of a stationary solution of a multidimensional reaction-diffusion equation with a discontinuous source, Computational Mathematics and Mathematical Physics, 2019, 59(4), 573-582. doi: 10.1134/S0965542519040109 [17] X. Lin, J. Liu and C. Wang, The existence, uniqueness and asymptotic estimates of solutions for third-order full nonlinear singularly perturbed vector boundary value problems, Boundary Value Problems, 2020, 14, 1-17. [18] X. Lin, J. Liu and C. Wang, The existence and asymptotic estimates of solutions for a third-order nonlinear singularly perturbed boundary value problem, Qualitative Theory of Dynamical Systems, 2019, 18, 687-710. doi: 10.1007/s12346-018-0307-y [19] D. V. Lukyanenko, M. A. Shishlenin and V. T. Volkov, Solving of the coefficient inverse problems for a nonlinear singularly perturbed reaction-diffusion-advection equation with the final time data, Communications in Nonlinear Science and Numerical Simulation, 2018, 54, 233-247. doi: 10.1016/j.cnsns.2017.06.002 [20] N. Nefedov, The existence and asymptotic stability of periodic solutions with an interior layer of Burgers type equations with modular advection, Math. Model. Natl. Phenom., 2019, 4(4), 1-14. [21] N. N. Nefedov and M. Ni, Internal layers in the one-dimensional reaction-diffusion equation with a discontinuous reactive term, Computational Mathematics and Mathematical Physics, 2015, 55(12), 2001-2007. doi: 10.1134/S096554251512012X [22] M. Ni, Y. Pang and N. T. Levashova, Internal layer for a system of singularly perturbed equations with discontinuous right-hand side, Differentsial'nye Uravneniya, 2018, 54(12), 1626-1637. [23] M. Ni, Y. Pang, N. T. Levashova and O. A. Nikolaeva, Internal layers for a singularly perturbed second-order quasilinear differential equation with discontinuous right-hand Side, Differential Equations, 2017, 53(12), 1616-1626. doi: 10.1134/S0012266117120096 [24] O. E. Omel'chenko, L. Recke and V. F. Butuzov, Time-periodic boundary layer solutions to singularly perturbed parabolic problems, Journal of Differential Equations, 2017, 262(9), 4823-4862. doi: 10.1016/j.jde.2016.12.020 [25] A. Orlov, N. Levashova and T. Burbaev, The use of asymptotic methods for modeling of the carriers wave functions in the Si/SiGe heterostructures with quantum-confined layers, Journal of Physics: Conference Series, 2015, 586(1), Article ID 012003. [26] A. B. Vasil'eva, Step-like contrasting structures for a singularly perturbed quasilinear second-order differential equation, Computational Mathematics and Mathematical Physics, 1995, 35(4), 411-419. [27] A. B. Vasil'eva and V. F. Butuzov, Asymptotic Methods in Singular Perturbation Theory, Moscow: Vysshaya Shkola, 1990. [28] A. B. Vasil'eva, V. F. Butuzov and L. V. Kalachev, The Boundary Function Method for Singular Perturbed Problem, SIAM Philadelphia, 1995. [29] A. B. Vasil'eva, V. F. Butuzov and N. N. Nefedov, Contrasting structures in singularly perturbed problems, Fundamentalnaya i Prikladnaya Matematika, 1998, 4(3), 799-851. [30] A. B. Vasil'eva, V. F. Butuzov and N. N. Nefedov, Singularly perturbed problems with boundary and internal layers, Proceedings of the Steklov Institute of Mathematics, 2010, 268, 258-273. doi: 10.1134/S0081543810010189 [31] V. T. Volkov, D. V. Luk'yanenko and N. N. Nefedov, Analytical-numerical approach to describing timeperiodic motion of fronts in singularly perturbed reaction-advection-diffusion models, Computational Mathematics and Mathematical Physics, 2019, 59(1), 46-58. doi: 10.1134/S0965542519010159 [32] V. T. Volkov and N. N. Nefedov, Development of the asymptotic method of differential inequalities for investigation of periodic contrast structures in reaction-diffusion equations, Computational Mathematics and Mathematical Physics, 2006, 46(4), 585-593. doi: 10.1134/S0965542506040075 [33] C. Wang and X. Zhang, Canards, heteroclinic and homoclinic orbits for a slow-fast predator-prey model of generalized Holling type Ⅲ, Journal of Differential Equations, 2019, 267, 3397-3441. doi: 10.1016/j.jde.2019.04.008 [34] Z. Zhou and J. Shen, Delayed phenomenon of loss of stability of solutions in a second-order quasi-linear singularly perturbed boundary value problem with a turning point, Boundary Value Problems, 2011, 2011(1), 1-13. doi: 10.1186/1687-2770-2011-1 -
-
- Figure 1. The illustration of solution to problem (1.1).
-
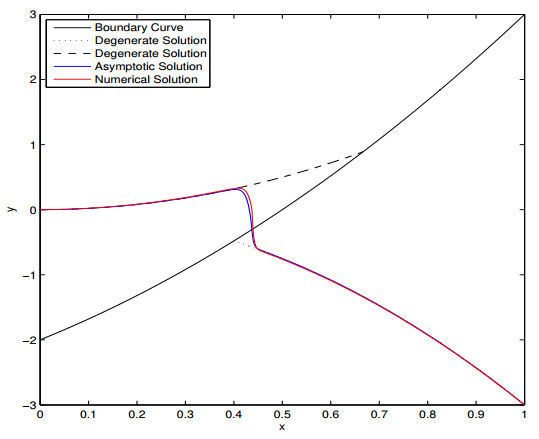
Figure 2. Numerical solution of problem (4.1) and its zero-order asymptotic approximation(
$ \mu = 0.001 $ ).





 DownLoad:
DownLoad: