| Citation: | Quting Chen, Yadong Shang, Huafei Di. BIFURCATIONS AND EXACT TRAVELING WAVE SOLUTIONS FOR THE GENERALIZED NONLINEAR SCHRÖDINGER EQUATION WITH WAVE OPERATOR[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 336-346. doi: 10.11948/20210216 |
BIFURCATIONS AND EXACT TRAVELING WAVE SOLUTIONS FOR THE GENERALIZED NONLINEAR SCHRÖDINGER EQUATION WITH WAVE OPERATOR
-
Abstract
In this paper, we investigate the dynamical bifurcations and exact traveling wave solutions for the generalized nonlinear Schrödinger equation with wave operator under different parametric conditions by means of the theory of singular system. We analyse the high order equilibrium point and give the phase portraits. We obtain many results under different values of the parameter $ p $ reflecting the strength of the nonlinearity in the model. For $ p = 1 $, we find explicit exact solutions of Jacobian elliptic functions type which is corresponding to the curves given by $ H(\phi, y) = h $. According to the qualitative analysis of the phase portraits, we give the conclusions on the existence of solitary wave solutions and periodic wave solutions when $ p\geq\frac{1}{2} $. In addition, we obtain the only explicit exact solitary wave solution corresponding to the curves given by $ H(\phi, y) = 0 $ for any $ p $. Especially, we obtain some explicit exact double periodic solutions of elliptic functions type for $ p = \frac{1}{2} $.
-

-
References
[1] J. V. Armitage, W.F. Eberlein, Elliptic Functions, London Mathematical Society, Student Texts 67, Springer-Verlag, Cambridge, 2006. [2] L. Brugnano, C. Zhang and D. Li, A class of energy-conserving Hamiltonian boundary value methods for nonlinear Schrödinger equation with wave operator, Commun. Nonlinear Sci. Numer. Simul., 2018, 60, 33–49. doi: 10.1016/j.cnsns.2017.12.018 [3] B. Guo, Initial-boundary value problem for one class of system of multidimensional nonlinear Schrödinger equations with wave operator, Sci. Sinica Ser. A, 1983, 26(6), 561–575. [4] B. Guo and H. Liang, On the problem of numerical calculation for a class of systems of nonlinear Schrödinger equations with wave operator, J. Numer. Methods Comput. Appl., 1983, 4(3), 176–182. [5] B. Guo, The "blow-up" problem for the system of nonlinear Schrödinger equations with wave operator and the soliton solution for the system, Sci. Exploration, 1985, 5(3), 93–98. [6] B. Guo, Existence and nonexistence for the initial-boundary value problem of one class of system of multidimensional nonlinear Schrödinger equations with operator and their soliton solutions, Acta Math. Sci. (English Ed. ), 1989, 9(1), 45–56. [7] L. Guo and Y. Xu, Energy conserving local discontinuous Galerkin methods for the nonlinear Schrödinger equation with wave operator, J. Sci. Comput., 2015, 65(2), 622–647. doi: 10.1007/s10915-014-9977-z [8] B. Ji and L. Zhang, An exponential wave integrator Fourier pseudospectral method for the nonlinear Schrödinger equation with wave operator, J. Appl. Math. Comput., 2018, 58(1–2), 273–288. doi: 10.1007/s12190-017-1144-x [9] K. Kou and J. Li, Bifurcations and exact traveling wave solutions of a modified nonlinear Schrödinger equation, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2016, 26(6), 1650106, 22 pp. [10] T. D. Leta and J. Li, Exact traveling wave solutions and bifurcations of the generalized derivative nonlinear Schrödinger equation, Nonlinear Dynam., 2016, 85(2), 1031–1037. doi: 10.1007/s11071-016-2741-1 [11] T. D. Leta and J. Li, Dynamical behavior and exact solution in invariant manifold for a septic derivative nonlinear Schrödinger equation, Nonlinear Dynam., 2017, 89(1), 509–529. doi: 10.1007/s11071-017-3468-3 [12] J. Li and H. Dai, On the study of singular nonlinear traveling wave equations: dynamical system approach, Science Press, China, Beijing, 2007. [13] J. Li, Bifurcations and exact solutions in invariant manifolds for nonlinear wave equations, Science Press, China, Beijing, 2019. [14] J. Li, Bifurcations and exact traveling wave solutions for a model of nonlinear pulse propagation in optical fibers, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2014, 24(6), 1450088, 15 pp. [15] J. Li and F. Chen, Breather solutions of a generalized nonlinear Schrödinger system, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2015, 25(8), 1550105, 16 pp. [16] J. Li, Exact solutions and bifurcations in invariant manifolds for a nonic derivative nonlinear Schrödinger equation, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2016, 26(8), 1650136, 32 pp. [17] J. Li and Y. Zhou, Bifurcations and exact traveling wave solutions for the nonlinear Schrödinger equation with fourth-order dispersion and dual power law nonlinearity, Discrete Contin. Dyn. Syst. Ser. S, 2020, 13(11), 3083–3097. [18] J. Li, G. Chen and Y. Zhou, Bifurcations and exact traveling wave solutions of two shallow water two-component systems, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2021, 31(1), 2150001, 13 pp. [19] J. Liang and J. Li, Bifurcations and exact solutions of nonlinear Schrödinger equation with an anticubic nonlinearity, J. Appl. Anal. Comput., 2018, 8(4), 1194–1210. [20] K. Matsuuchi, Nonlinear interactions of counter-travelling waves, J. Phys. Soc. Japan, 1980, 48(5), 1746–1754. doi: 10.1143/JPSJ.48.1746 [21] J. Wang, Multisymplectic fourier pseudospectral method for the nonlinear Schrödinger equations with wave operator, J. Comput. Math., 2007, 25(1), 31–48. [22] L. Wang, L. Kong and L. Zhang et al., Multi-symplectic preserving integrator for the Schrödinger equation with wave operator, Appl. Math. Model., 2015, 39(22), 6817–6829. doi: 10.1016/j.apm.2015.01.068 [23] T. Wang and L. Zhang, Analysis of some new conservative schemes for nonlinear Schrödinger equation with wave operator, Appl. Math. Comput. , 2006, 182(2), 1780–1794. [24] X. Zhao, A combination of multiscale time integrator and two-scale formulation for the nonlinear Schrödinger equation with wave operator, J. Comput. Appl. Math., 2017, 326, 320–336. doi: 10.1016/j.cam.2017.06.006 -
-
-
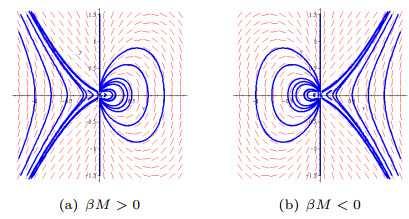
Figure 1. The bifurcations of phase portraits of system
$ (2.11) $ for$ N\neq0 $ -
Figure 2. The bifurcations of phase portraits of system
$ (2.11) $ for$ N=0 $





 DownLoad:
DownLoad: