| Citation: | Hao Wen, Shang Wu, Hongfu Yang, Jianhua Huang. SYNCHRONIZATION OF THE RÖSSLER-LORENZ SYSTEMS WITH FRACTIONAL BROWNIAN MOTION[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1727-1747. doi: 10.11948/20210219 |
SYNCHRONIZATION OF THE RÖSSLER-LORENZ SYSTEMS WITH FRACTIONAL BROWNIAN MOTION
-
Abstract
The current paper is devoted to the dynamics of stochastic chaotic systems with fractional Brownian motion with $H\in(\frac{1}{2}, 1)$. The existence and uniqueness of the so-called stochastic Rössler-Lorenz system driven by fractional Brownian motion is established. Moreover, the stochastic synchronization of stochastic Rössler-Lorenz system is proved, and some numerical simulations are provided to verify the theoretical results.
-
Keywords:
- Fractional Brownian motion /
- Rössler-Lorenz system /
- synchronization
-

-
References
[1] Z. Chen, W. Lin and J. Zhou, Complete and generalized synchronization in a class of noise perturbed chaotic systems, Chaos, 2007, 17(2), 023106. doi: 10.1063/1.2718491 [2] M. Diop and M. J. Garrido, Retarded evolution systems driven by fractional Brownian motion with Hurst parameter $H>\frac{1}{2}$, Nonlinear Anal. Theory Methods Appl., 2014, 97, 15–29. doi: 10.1016/j.na.2013.11.008 [3] K. Elworthy and X. Li, Formulae for the Derivatives of Heat Semigroups, J. Funct. Anal., 1994, 125(1), 252–286. doi: 10.1006/jfan.1994.1124 [4] M. Fernique, Intégrabilité des Vecteurs Gaussiens, C. R. Acad. Sci. Paris Sér. A–B, 1970, 270(1), A1698–A1699. [5] M. Hairer, Ergodicity of Stochastic Differential Equations Driven by Fractional Brownian Motion, Ann. Probab., 2005, 33(2), 703–758. [6] M. Hairer and A. Ohashi, Ergodic theory for SDEs with extrinsic memory, Ann. Probab., 2007, 35(5), 1950–1977. [7] Y. Hou, Z. Wan and T. Liao, Finite-time synchronization of switched stochastic Rössler systems, Nonlinear Dynam., 2012, 70(1), 315–322. doi: 10.1007/s11071-012-0456-5 [8] Y. Hu and D. Nualart, Differential Equations Driven by Hölder Continuous Functions of Order Greater than 1/2, Stoch. Anal. Appl., 2007, 2(1), 399–413. [9] S. Jiang and J. Yin, Global existence, uniqueness and pathwise property of solutions to a stochastic Rössler-Lorentz system, Chin. Ann. Math. Ser. B, 2015, 36(1), 105–124. doi: 10.1007/s11401-014-0872-6 [10] E. Knobloch, Chaos in the segmented disc dynamo, Phys. Lett. A, 1981, 82(9), 439–440. doi: 10.1016/0375-9601(81)90274-7 [11] E. Lorenz, Deterministic nonperiodic flow, J. Atmos. Sci., 1963, 20, 130–141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [12] B. Mandelbrot and J. Van Ness, Fractional Brownian motion, fractional noises and applications, SIAM Rev., 1968, 10(4), 422–437. doi: 10.1137/1010093 [13] X. Mao, The truncated Euler-Maruyama method for stochastic differential equations, J. Comput. Appl. Math., 2015, 290, 370–384. doi: 10.1016/j.cam.2015.06.002 [14] Y. Mishura, Stochastic Calculus for Fractional Brownian Motion and Related Processes, Springer International Publishing, Berlin, 2008. [15] D. Nualart and A. Rǎşcanu, Differential equations driven by fractional Brownian motion, Collect. Math., 2002, 53(1), 55–81. [16] I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999. [17] O. E. Rössler, An equation for continuous chaos, Phys. Lett. A, 1976, 57(5), 397–398. doi: 10.1016/0375-9601(76)90101-8 [18] G. Samorodnitsky and M. S. Taqqu, Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance, CRC Press, London, 1994. [19] P. Xu, J. Huang and C. Zeng, Ergodicity of stochastic Rabinovich systems driven by fractional Brownian motion, Phys. A, 2020, 546, 122955. doi: 10.1016/j.physa.2019.122955 [20] Q. Yang and D. Jiang, A note on asymptotic behaviors of stochastic population model with Allee effect, Appl. Math. Modelling, 2011, 35(9), 4611–4619. doi: 10.1016/j.apm.2011.03.034 [21] C. Zeng and Q. Yang, Dynamics of the stochastic Lorenz chaotic system with long memory effects, Chaos, 2015, 25(12), 123114. doi: 10.1063/1.4937726 [22] W. Zhou, X. Zhou, J. Yang, Y. Liu, X. Zhang and X. Ding, Exponential synchronization for stochastic neural networks driven by fractional Brownian motion, J. Frankl. Inst., 2016, 353(8), 1689–1712. doi: 10.1016/j.jfranklin.2016.02.019 -
-
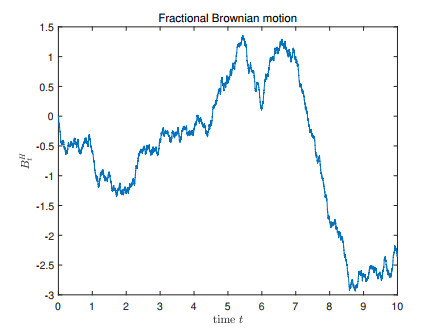
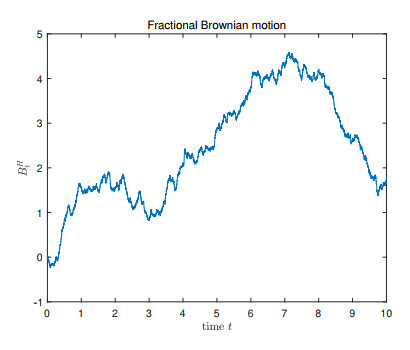
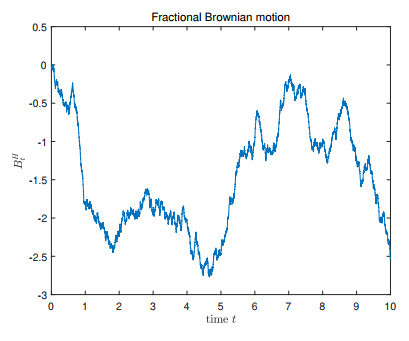
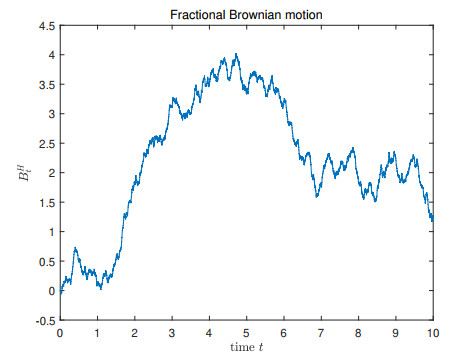
- Figure 1. Trajectory of fBm
-
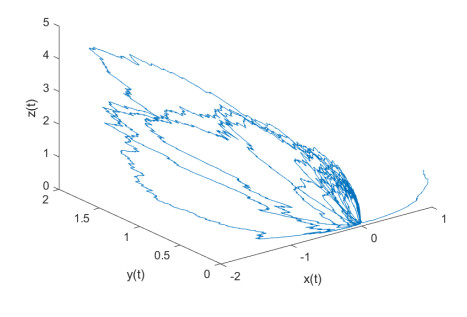
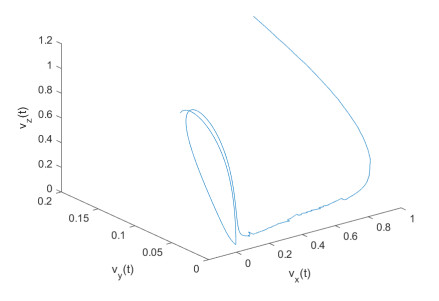
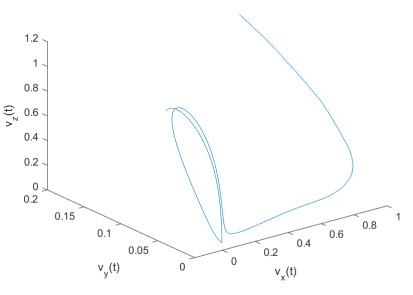
Figure 2. Sample path of Example 2.1 with
$ k_i=1 $ ,$ i=1, 2, 3 $ -
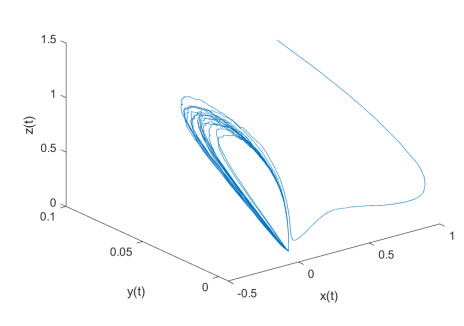
Figure 3. Sample path of Example 2.1 with
$ k_i=0.1 $ ,$ i=1, 2, 3 $ -
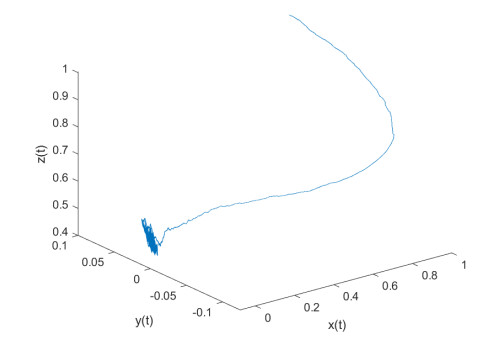
Figure 4. Sample path of Example 2.2 with
$ k_i=1 $ ,$ i=1, 2, 3 $ -
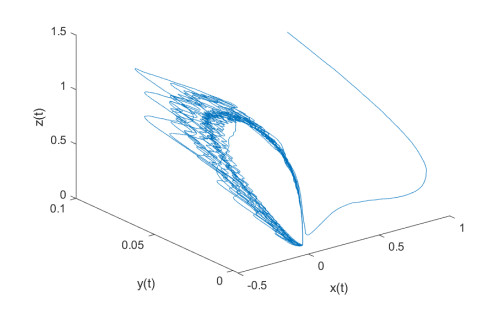
Figure 5. Sample path of Example 2.2 with
$ k_i=0.1 $ ,$ i=1, 2, 3 $ - Figure 6. Trajectory of fBm
-
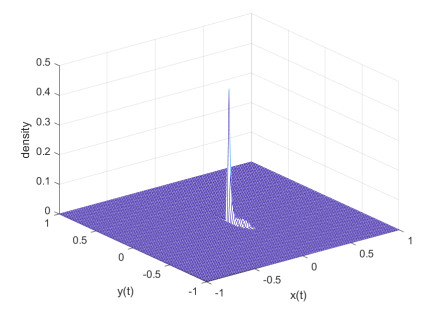
Figure 7.
$ \eta $ in XY space -
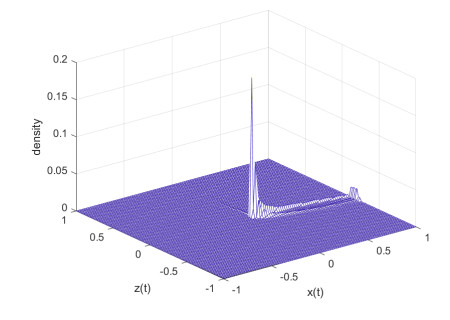
Figure 8.
$ \eta $ in XZ space -
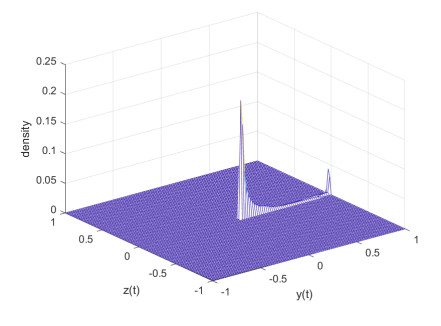
Figure 9.
$ \eta $ in YZ space - Figure 10. Trajectory of fBm
- Figure 11. Sample path of response system
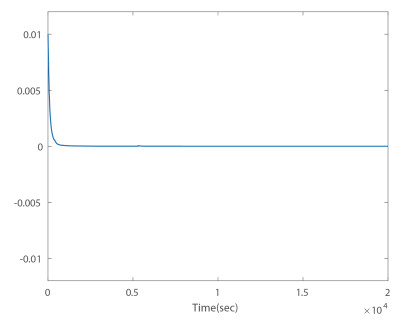
- Figure 12. Time responses of the synchronization error
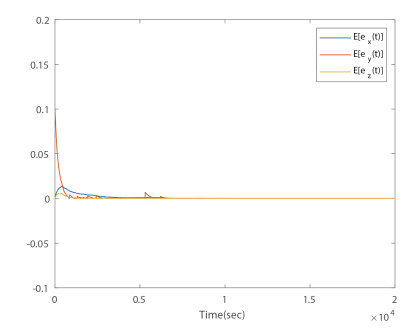
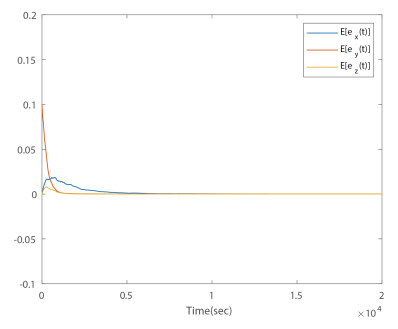
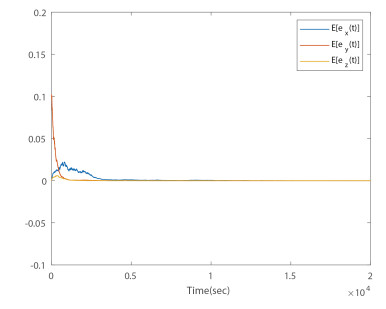
- Figure 13. Time responses of mean values
- Figure 14. Trajectory of fBm
- Figure 15. Sample path of response system
- Figure 16. Time responses of the synchronization error
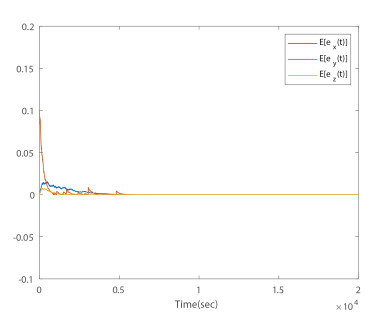
- Figure 17. Time responses of mean values
-
Figure 18. Times responses with controller
$ \Gamma $ -
Figure 19. Times responses with controller
$ \tilde{\Gamma} $




 DownLoad:
DownLoad: