| Citation: |
Nan Cao, Xianlong Fu. STATIONARY DISTRIBUTION OF A LOTKA-VOLTERRA MODEL WITH STOCHASTIC PERTURBATIONS AND DISTRIBUTED DELAY[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1713-1726. doi: 10.11948/20210175
|
STATIONARY DISTRIBUTION OF A LOTKA-VOLTERRA MODEL WITH STOCHASTIC PERTURBATIONS AND DISTRIBUTED DELAY
-
Abstract
This paper devotes to the existence of a stationary distribution for a one-prey and two-predator Lotka-Volterra model with stochastic nonlinear perturbations and distributed delay. The studied autonomous system is first proved having a unique global and positive solution. Then, through constructing appropriate Lyapunov function and using Itô formula, sufficient conditions guaranteeing the existence of a stationary distribution of the stochastic system are obtained. Some numerical simulations are also provided in the end to illustrate the main results.
-
Keywords:
- Lotka-Volterra model /
- Itô formula /
- global solution /
- stationary distribution /
- distributed delay
-
-
References
[1] J. Alebraheem and Y. Hasan, Dynamics of a two predator-one prey system, Comp. Appl. Math., 2014, 33(3), 767–780. doi: 10.1007/s40314-013-0093-8 [2] A. Bahar and X. Mao, Stochastic delay Lotka-Volterra model, J. Math. Anal. Appl., 2004, 292(2), 364–380. doi: 10.1016/j.jmaa.2003.12.004 [3] K. Blyuss and Y. Kyrychko, Stability and bifurcations in an epidemic model with varying immunity period, Bull. Math. Biol., 2010, 72(2), 490–505. doi: 10.1007/s11538-009-9458-y [4] Y. Cai, S. Cai and X. Mao, Analysis of a stochastic predator-prey system with foraging arena scheme, Stochastics, 2020, 92(2), 193–222. doi: 10.1080/17442508.2019.1612897 [5] Z. Cao, W. Feng, X. Wen and L. Zu, Stationary distribution of a stochastic predator-prey model with distributed delay and higher order perturbations, Phys. A, 2019, 521, 467–475. doi: 10.1016/j.physa.2019.01.058 [6] J. Cushing, Periodic time-dependent predator-prey systems, SIAM J. Appl. Math., 1977, 32(1), 82–95. doi: 10.1137/0132006 [7] L. Dai, Nonconstant periodic solutions in predator-prey systems with continuous time delay, Math. Biosc., 1981, 53 (1–2), 149–157. doi: 10.1016/0025-5564(81)90044-4 [8] B. Dubey and R. Upadhyay, Persistence and extinction of one-prey and two-predators system, Nonl. Anal. (MC), 2004, 9(4), 307–329. [9] M. Farkas and H. Freedman, Stability conditions for two predator one prey systems, Acta Appl. Math., 1989, 14(1–2), 3–10. doi: 10.1007/BF00046669 [10] J. Geng, M. Liu and Y. Zhang, Stability of a stochastic one-predator-two-prey population model with time delays, Comm. Nonl. Sci. Num. Sim., 2017, 53, 65–82. doi: 10.1016/j.cnsns.2017.04.022 [11] L. Jaume and D. Xiao, Global dynamics of a Lotka-Volterra model with two predators competing for one prey, SIAM J. Appl. Math., 2014, 74(2), 434–453. doi: 10.1137/130923907 [12] C. Ji, D. Jiang, H. Liu and Q. Yang, Existence, uniqueness and ergodicity of positive solution of mutualism system with stochastic perturbation, Math. Prob. Eng., 2010. DOI:10.1155/2010/684926. [13] C. Ji, D. Jiang and N. Shi, Analysis of a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes with stochastic perturbation, J. Math. Anal. Appl., 2009, 359(2), 482–498. doi: 10.1016/j.jmaa.2009.05.039 [14] C. Ji, X. Yang and Y. Li, Permanence, extinction and periodicity to a stochastic competitive model with infinite distributed delays, J. Dyn. Diff. Equ., 2021, 33(1), 135–176. doi: 10.1007/s10884-020-09850-7 [15] R. Khasminskii, Stochastic stability of differential equations, Springer, Heidelberg, 2012. [16] Y. Kuang, Delay differential equations with applications in population dynamics, Academic Press, Boston, 1993. [17] Q. Liu, Y. Liu and X. Pan, Global stability of a stochastic predator-prey system with infinite delays, Appl. Math. Comp., 2014, 235, 1–7. doi: 10.1016/j.amc.2014.02.091 [18] Q. Liu and D. Jiang, Stationary distribution and extinction of a stochastic predator-prey model with distributed delay, Appl. Math. Letters, 2018, 78, 79–87. doi: 10.1016/j.aml.2017.11.008 [19] Q. Liu and D. Jiang, Periodic solution and stationary distribution of stochastic predator-prey models with higher-order perturbation, J. Nonl. Sci., 2018, 28, 423–442. doi: 10.1007/s00332-017-9413-2 [20] Q. Liu, D. Jiang, T. Hayat and B. Ahmad, Stationary distribution and extinction of a stochastic predator-prey model with additional food and nonlinear perturbation, Appl. Math. Comp., 2018, 320, 226–239. doi: 10.1016/j.amc.2017.09.030 [21] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Long-time behavior of a stochastic logistic equation with distributed delay and nonlinear perturbation, Phys. A, 2018, 508, 289–304. doi: 10.1016/j.physa.2018.05.054 [22] Q. Liu, D. Jiang, N. Shi, T. Hayat and A. Alsaedi, Dynamical behavior of a stochastic HBV infection model with logistic hepatocyte growth, Acta Math. Sci. Ser. B, 2017, 37(4), 927–940. doi: 10.1016/S0252-9602(17)30048-6 [23] H. Li and Y. Takeuchi, Dynamics of the density dependent predator-prey system with Beddington-DeAngelis functional response, J. Math. Anal. Appl., 2011, 374(2), 644–654. doi: 10.1016/j.jmaa.2010.08.029 [24] M. Liu and K. Wang, Population dynamical behavior of Lotka-Volterra cooperative systems with random perturbations, Disc. Cont. Dyn. Syst., 2013, 33(6), 2495–2522. doi: 10.3934/dcds.2013.33.2495 [25] N. MacDonald, Time lags in biological models, Springer-Verlag, New York, 1978. [26] X. Mao, Stationary distribution of stochastic population systems, Syst. Control Lett., 2011, 60(6), 398–405. doi: 10.1016/j.sysconle.2011.02.013 [27] X. Mao and C. Yuan, Stochastic Differential Equations with Markovian Switching, Imperial College Press, London, 2006. [28] G. Maruyama, Continuous Markov processes and stochatic equations, Rend. Circ. Mat. Palermo, 1995. DOI:10.1007/BF02846028. [29] S. Ruan, Delay differential equations in single species dynamics, in: O. Arino, M. Hbid, E. Ait Dads (Eds. ), Delay Diff. Equ. and Appl., Springer, Berlin, 2006, 205, 477–517. [30] A. Ventcel and M. Freidlin, Small random perturbations of dynamical systems, Uspehi Mat. Nauk, 1970, 25(1), 3–55. [31] J. Wu, Analysis of a three-species stochastic delay predator-prey system with imprecise parameters, Meth. Comp. Appl. Prob., 2019, 21(1), 43–67. doi: 10.1007/s11009-018-9640-5 [32] D. Xu, Y. Huang and Z. Yang, Existence theorems for periodic Markov process and stochastic functional differential equations, Discr. Cont. Dyn. Syst., 2009, 24(3), 1005–1023. doi: 10.3934/dcds.2009.24.1005 [33] Y. Zhang, S. Chen and S. Gao, Analysis of a nonautonomous stochastic predator-prey model with Crowley-Martin functional response, Adv. Diff. Equ., 2016. DOI:10.1186/s13662-016-0993-1. [34] Y. Zhang, K. Fan, S. Gao and S. Chen, A remark on stationary distribution of a stochastic SIR epidemic model with double saturated rates, Appl. Math. Lett., 2018, 76, 46–52. doi: 10.1016/j.aml.2017.08.002 [35] Q. Zhang, D. Jiang, Z. Liu and D. O'Regan, The long time behavior of a predator-prey model with disease in the prey by stochastic perturbation, Appl. Math. Comp., 2014, 245, 305–320. doi: 10.1016/j.amc.2014.07.088 [36] X. Zhao and Z. Zeng, Stationary distribution of a stochastic predator-prey system with stage structure for prey, Phys. A, 2020, 545, 12. [37] X. Zhao and Z. Zeng, Stationary distribution and extinction of a stochastic ratio-dependent predator-prey system with stage structure for the predator, Phys. A, 2020, 545, 17. [38] W. Zuo, D. Jiang, X. Sun, T. Hayat and A. Alsaedi, Long-time behaviors of a stochastic cooperative Lotka-Volterra system with distributed delay, Phys. A, 2018, 506, 542–559. doi: 10.1016/j.physa.2018.03.071 -
-
Figures(1)
Export File
Citation
Nan Cao, Xianlong Fu. STATIONARY DISTRIBUTION OF A LOTKA-VOLTERRA MODEL WITH STOCHASTIC PERTURBATIONS AND DISTRIBUTED DELAY[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1713-1726. doi: 10.11948/20210175
Format
Content
DownLoad:
-
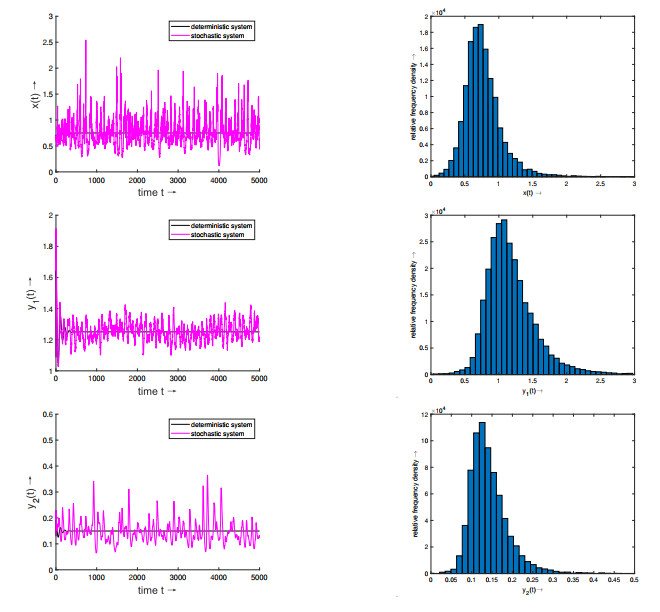
Figure 1. The left is the solution of the stochastic system (1.3) and the corresponding deterministic system. The right is the density function of
$ x(t) $ ,$ y_{1}(t) $ and$ y_{2}(t) $ for the system (1.3) obtained by 10, 000 simulations running at$ t=200 $ .