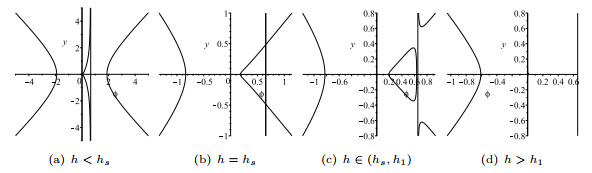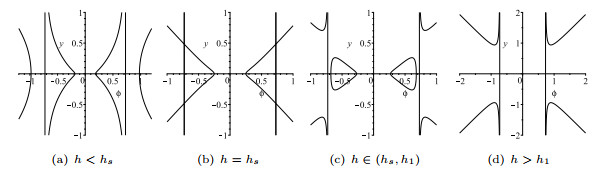| Citation: |
Yan Zhou, Jibin Li. BIFURCATIONS OF TRAVELING WAVE SOLUTIONS IN THE HOMOGENEOUS CAMASSA-HOLM TYPE EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 392-406. doi: 10.11948/20210256
|
BIFURCATIONS OF TRAVELING WAVE SOLUTIONS IN THE HOMOGENEOUS CAMASSA-HOLM TYPE EQUATIONS
-
Abstract
This paper studies traveling wave solutions of the homogeneous Camassa-Holm type equations introduced by Hay et al. in 2019. Under given parameter conditions, the corresponding traveling system is a singular system of the first class defined by [
16 ]. The bifurcations of traveling wave solutions in the parameter space are investigated from the perspective of dynamical systems. The existence of solitary wave solution, periodic peakon solution and peakon, pseudo-peakon as well as compacton solution is proved. Possible exact explicit parametric representations of various solutions are given.-
Keywords:
- Solitary wave /
- peakon /
- pseudo-peakon /
- periodic peakon /
- compacton /
- bifurcation /
- Camassa-Holm type equation
-
-
References
[1] S. C. Anco, P. L. da Silva and I. L. Freire, A family of wave-breaking equations generalizing the Camassa-Holm and Novikov equations, J. Math. Phys., 2015, 56, 091506. doi: 10.1063/1.4929661 [2] S. C. Anco, E. Recio, M. L. Gandarias and M. S. Bruzon, A nonlinear generalization of the Camassa-Holm equation with peakon solutions Dynamical Systems, Differential Equations and Applications (Proc. 10th AIMS Int. Conf. ) (Spain), 2015, 29-37. [3] S. C. Anco and D. Kraus, Hamiltonian structure of peakons as weak solutions for the modified Camassa-Holm equation, Discrete Continuous Dyn. Syst. A, 2018, 38, 4449-4465. doi: 10.3934/dcds.2018194 [4] S. C. Anco and E. Recio, Accelerating dynamical peakons and their behaviour, Discrete Continuous Dyn. Syst. A., 2018, 39, 6131-6148. [5] S. C. Anco and E. Recio, Conserved norms and related conservation laws for multi-peakon equations, J. Phys. A: Math. Theor., 2018, 51, 065203. doi: 10.1088/1751-8121/aaa0e0 [6] S. C. Anco and E. Recio, A general family of multi-peakon equations and their properties, J. Phys. A: Math. Theor., 2019, 52, 125203. doi: 10.1088/1751-8121/ab03dd [7] A. Arai, Exactly solvable supersymmetric quantum mechanics, J. Math. Anal. Appl., 1991, 158, 63-79. doi: 10.1016/0022-247X(91)90267-4 [8] A. Arai, Exact solutions of multi-component nonlinear Schrödinger and Klein-Gordon equations in two-dimensional space-time, J. Phys. A: Math. Gen., 2001, 34, 4281. doi: 10.1088/0305-4470/34/20/302 [9] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971. [10] R. Camassa and D. D. Holm, An integrable shallow water equation with peak solutions, Phys. Rev. Lett., 1993, 71(11), 1161-1164. [11] R. Camassa, D. D. Holm and J. M. Hyman, A new integrable shallow water equation, Adv. Appl. Mech., 1994, 31, 1-33. [12] R. Camassa, J. M. Hyman and B. P. Luce, Nonlinear waves and solitons in physical sysytems, Phys. D., 1998, 123(1-4), 1-20. doi: 10.1016/S0167-2789(98)00108-0 [13] K. Grayshan and A. Himonas, Equations with peakon traveling wave solutions, Adv. Dyn. Syst. Appl., 2013, 8, 217-232. [14] M. Hay, N. W. Andrew, A. N. W. Hone, V. S. Novikov and J. Wan, Remarks on certain two-component systems with peakon solutions, J. Geom. Mech., 2019, 11(4), 561-573. doi: 10.3934/jgm.2019028 [15] A. Himonas and Mantzavinos, An ab-family of equations with peakon travelling waves, Proc. Am. Math. Soc., 2016, 144, 3797-811. [16] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifur. Chaos., 2007, 17, 4049-4065. doi: 10.1142/S0218127407019858 [17] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [18] J. Li and Z. Qiao, Bifurcations and exact travelling wave solutions of the generalized two-component Camassa-Holm equation, Int. J. Bifur. Chaos., 2012, 22, 1250305. doi: 10.1142/S0218127412503051 [19] J. Li, Variform exact one-peakon solutions for some singular nonlinear traveling wave equations of the first kind, Int. J. Bifur. Chaos., 2014, 24, 1450160. doi: 10.1142/S0218127414501600 [20] J. Li, W. Zhu and G. Chen, Understanding peakons, periodic peakons and compactons via a shallow water wave equation, Int. J. Bifur. Chaos., 2016, 26, 1650207. doi: 10.1142/S0218127416502072 -
-
Figures(9)
Export File
Citation
Yan Zhou, Jibin Li. BIFURCATIONS OF TRAVELING WAVE SOLUTIONS IN THE HOMOGENEOUS CAMASSA-HOLM TYPE EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 392-406. doi: 10.11948/20210256
Format
Content
DownLoad:
-
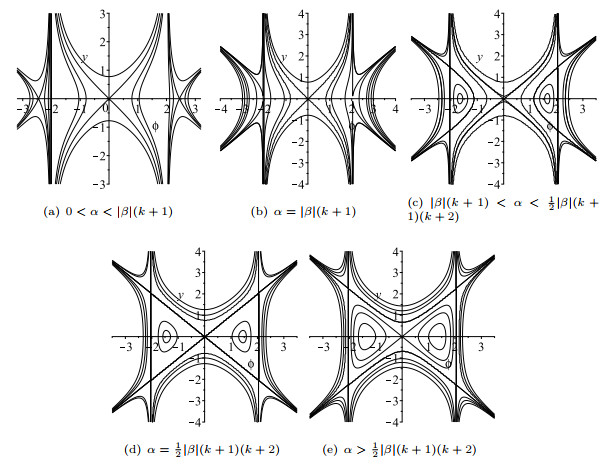
Figure 1. The bifurcations of phase portraits of system (1.7) for
$ \beta<0,\tilde{\delta}>0 $ ,$ k $ is odd. -
Figure 2. The bifurcations of phase portraits of system (1.7) for
$ \tilde{\delta} = \frac12k\beta $ , and$ k $ is even. -
Figure 3. The bifurcations of phase portraits of system (1.7) for
$ \tilde{\delta} = \frac12k\beta $ , and$ k $ is odd. -
Figure 4. The bifurcations of phase portraits of system (1.8) for
$ \tilde{\delta} = -\frac12p\beta $ , and$ p $ is odd. -
Figure 5. The bifurcations of phase portraits of system (1.8) for
$ \tilde{\delta} = -\frac12p\beta $ , and$ p $ is even. -
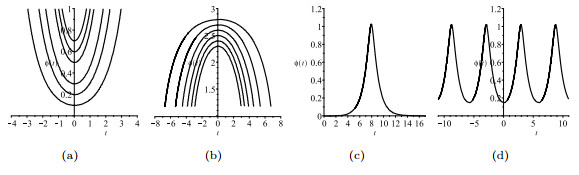
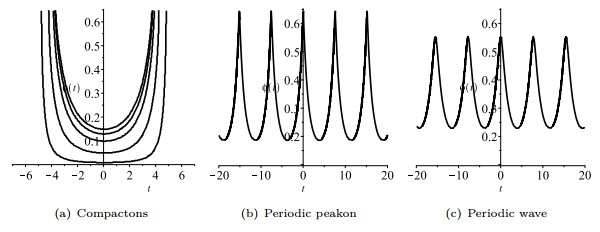
Figure 6. The profiles of compactons and solitary wave solution of (1.4) for
$ \beta\tilde{\delta}<0 $ . -
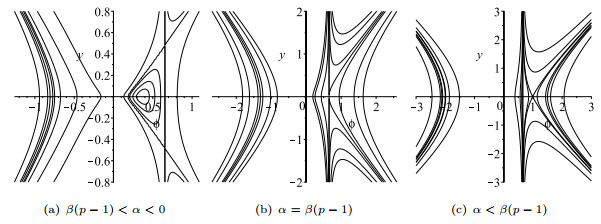
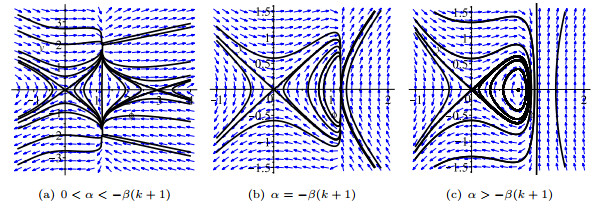
Figure 7. The level curves
$ H_{20}(\phi,y) = h $ of equation (1.8) for$ \beta(p-1)<\alpha<0 $ . -
Figure 8. Profiles of equation (1.8) for
$ \beta(p-1)<\alpha<0 $ . -
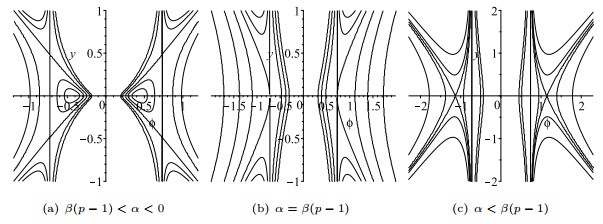
Figure 9. The level curves
$ H_{20}(\phi,y) = h $ of equation (1.8) for$ \beta(p-1)<\alpha<0 $ .