| Citation: |
Hai-Feng Huo, Kai-Di Cao, Hong Xiang. MODELLING THE EFFECTS OF THE VACCINATION ON SEASONAL INFLUENZA IN GANSU, CHINA[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 407-435. doi: 10.11948/20210306
|
MODELLING THE EFFECTS OF THE VACCINATION ON SEASONAL INFLUENZA IN GANSU, CHINA
-
Abstract
Seasonal influenza is still prevalent and poses a huge health burden, which is the most worth considerable issue that causes economic pressure on the government. Investigating the essential characteristics of seasonal influenza can assist to improve people's vigilance. A new influenza model with vaccination and periodic transmission rate is introduced in this essay. The basic reproduction number R0 is derived, and formulate that R0 is an important indicator to measure whether seasonal influenza can spread in the population. Furthermore, the explicit consequences for the implementation of optimal control and the corresponding optimal solutions to alleviate the spread of influenza virus are explored and derived. The best fitting parameters in our model are determined from the seasonal influenza case data reported in Gansu Province via MCMC procedure. The value of R0 is 1.2266(95%CI: (1.2230, 1.2302)) by estimating unknown parameters. The different vigorous control strategies for controlling the transmission of seasonal influenza are also studied and simulated. Finally, the uncertainty and sensitivity of some parameters are shown to determine which critical control strategy is effective. Our numerical results imply that raising the vaccination rate can availably reduce the spread of seasonal influenza in Gansu Province, and vaccination is a more effective method than treatment.
-
Keywords:
- Influenza /
- parameter estimation /
- sensitivity analysis /
- optimal control /
- vaccination
-
-
References
[1] Gansu Provincial Bureau of Statistics, http://tjj.gansu.gov.cn/. 2021. [2] Gansu Provincial Center for Disease Control and Prevention, http://www.gscdc.net/. 2021. [3] National Bureau of Statistics of People's Republic of China, Annual Statistics of Gansu Province, http://www.stats.gov.cn/. 2021. [4] G. Aronsson and R. Kellogg, On a differential equation arising from compartmental analysis, Math. Biosci., 1978, 38(1–2), 113–122. doi: 10.1016/0025-5564(78)90021-4 [5] Y. Cai, S. Zhao, Y. Niu et al., Modelling the effects of the contaminated environments on tuberculosis in Jiangsu, China, J. Theor. Biol., 2021, 508, 1–12. [6] L. Cao, J. Lou, S. Zhao et al., In silico prediction of influenza vaccine effectiveness by sequence analysis, Vaccine, 2021, 39(7), 1030–1034. doi: 10.1016/j.vaccine.2021.01.006 [7] R. Casagrandi, L. Bolzoni, S. A. Levin and V. Andreasen, The SIRC model and influenza A, Math. Biosci., 2006, 200(2), 152–169. doi: 10.1016/j.mbs.2005.12.029 [8] D. Dwyer, I. Barr, A. Hurt et al., Seasonal influenza vaccine policies, recommendations and use in the World Health Organization's Western Pacific Region, Western Pac. Surveill. Response J., 2013, 4(3), 51–59. [9] D. J. Earn, J. Dushoff and S. A. Levin, Ecology and evolution of the flu, Trends Ecol. Evol., 2002, 17(7), 334–340. doi: 10.1016/S0169-5347(02)02502-8 [10] W. H. Fleming and R. W. Rishel, Deterministic and Stochastic Optimal Control, Springer, Berlin, Germany, 2012. [11] G. He, J. Wang and G. Huang, Threshold dynamics of an epidemic model with latency and vaccination in a heterogeneous habitat, J. Non. Model. Anal., 2020, 2(3), 393–410. [12] H. W. Hethcote, The mathematics of infectious diseases, SIAM Rev., 2000, 42(4), 599–653. doi: 10.1137/S0036144500371907 [13] M. W. Hirsch, Systems of differential equations that are competitive or cooperative ii: Convergence almost everywhere, SIAM J. Math. Anal., 1985, 16(3), 423–439. doi: 10.1137/0516030 [14] S. H. Ho, D. He and R. Eftimie, Mathematical models of transmission dynamics and vaccine strategies in Hong Kong during the 2017–2018 winter influenza season, J. Theor. Biol., 2019, 476, 74–94. doi: 10.1016/j.jtbi.2019.05.013 [15] M. A. Ibrahim and A. Dénes, A mathematical model for Lassa fever transmission dynamics in a seasonal environment with a view to the 2017–20 epidemic in Nigeria, Nonlinear Anal. RWA., 2021, 60, 1–21. [16] M. A. Ibrahim and A. Dénes, Threshold dynamics in a model for Zika virus disease with seasonality, B. Math. Biol., 2021, 83(4), 1–28. [17] S. Jing, H. Huo and H. Xiang, Modeling the effects of meteorological factors and unreported cases on seasonal influenza outbreaks in Gansu province, China, B. Math. Biol., 2020, 82(6), 1–36. [18] S. Jing, H. Huo and H. Xiang, Modelling the effects of ozone concentration and pulse vaccination on seasonal influenza outbreaks in Gansu Province, China, Discrete Cont. Dyn-B., 2021. DOI: 10.3934/dcdsb.2021113. [19] E. D. Kilbourne, Influenza pandemics of the 20th century, Emerg. Infect. Dis., 2006, 12(1), 9–14. doi: 10.3201/eid1201.051254 [20] S. Kim and E. Jung, Prioritization of vaccine strategy using an age-dependent mathematical model for 2009 A/H1N1 influenza in the Republic of Korea, J. Theor. Biol., 2019, 479, 97–105. doi: 10.1016/j.jtbi.2019.07.011 [21] P. Macdonald and J. Lyth, Incubation period of influenza, Brit. Med. J., 1918, 2(3018), 488. [22] E. Massad, M. N. Burattini, F. A. B. Coutinho and L. F. Lopez, The 1918 influenza A epidemic in the city of Sao Paulo, Brazil, Med. Hypotheses, 2007, 68(2), 442–445. doi: 10.1016/j.mehy.2006.07.041 [23] L. Perko, Differential Equations and Dynamical Systems, Springer Science & Business Media, New York, 2013. [24] J. B. Plotkin, J. Dushoff and S. A. Levin, Hemagglutinin sequence clusters and the antigenic evolution of influenza A virus, P. Natl. Acad. Sci., 2002, 99(9), 6263–6268. doi: 10.1073/pnas.082110799 [25] L. S. Pontryagin, Mathematical Theory of Optimal Processes, Routledge, London, 2018. [26] M. J. Postma, R. P. M. Baltussen, A. M. Palache and J. C. Wilschut, Further evidence for favorable cost-effectiveness of elderly influenza vaccination, Expert. Rev. Pharm. Out., 2006, 6(2), 215–227. [27] L. A. Prosser, C. B. Bridges, T. M. Uyeki et al., Health benefits, risks, and cost-effectiveness of influenza vaccination of children, Emerg. Infect. Dis., 2006, 12(10), 1548–1558. doi: 10.3201/eid1210.051015 [28] Z. Qiu and Z. Feng, Transmission dynamics of an influenza model with vaccination and antiviral treatment, B. Math. Biol., 2010, 72(1), 1–33. doi: 10.1007/s11538-009-9435-5 [29] L. Shi, H. Zhao and D. Wu, Modeling Periodic HFMD with the Effect of Vaccination in Mainland China, Complexity, 2020, 2020, 1–18. [30] H. L. Smith and P. Waltman, The Theory of the Chemostat: Dynamics of Microbial Competition, Cambridge university press, Cambridge, 1995. [31] H. R. Thieme, Convergence results and a Poincaré-bendixson trichotomy for asymptotically autonomous differential equations, J. Math. Biol., 1992, 30(7), 755–763. [32] J. Wang, Y. Xiao and Z. Peng, Modelling seasonal HFMD infections with the effects of contaminated environments in mainland China, Appl. Math. Comput, 2016, 274, 615–627. [33] W. Wang and X. Zhao, Threshold dynamics for compartmental epidemic models in periodic environments, J. Dyn. Differ. Equ., 2008, 20(3), 699–717. doi: 10.1007/s10884-008-9111-8 [34] Y. Xing, L. Song, G. Sun et al., Assessing reappearance factors of H7N9 avian influenza in China, Appl. Math. Comput., 2017, 309, 192–204. [35] F. Zhang and X. Zhao, A periodic epidemic model in a patchy environment, J. Math. Anal. Appl., 2007, 325(1), 496–516. doi: 10.1016/j.jmaa.2006.01.085 [36] J. Zhang, Y. Li, Z. Jin and H. Zhu, Dynamics analysis of an avian influenza A (H7N9) epidemic model with vaccination and seasonality, Complexity, 2019, 2019, 1–15. [37] X. Zhao, Dynamical Systems in Population Biology, Second Springer, New York, 2017. [38] Y. Zhu, B. Xu, X. Lian et al., A hand-foot-and-mouth disease model with periodic transmission rate in Wenzhou, China, Abstr. Appl. Anal., 2014, 2014, 1–11. -
-
Figures(19) / Tables(2)
Export File
Citation
Hai-Feng Huo, Kai-Di Cao, Hong Xiang. MODELLING THE EFFECTS OF THE VACCINATION ON SEASONAL INFLUENZA IN GANSU, CHINA[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 407-435. doi: 10.11948/20210306
Format
Content
DownLoad:
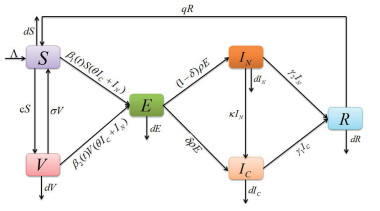
- Figure 1. The schematic diagram for the dynamics of influenza system (2.1).
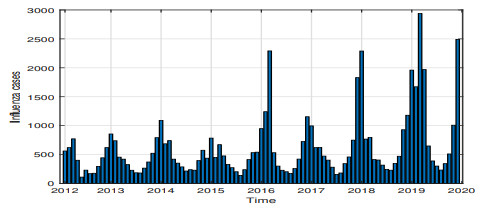
- Figure 2. Number of monthly cases of seasonal influenza revealed by Gansu CDC from January 2012 to December 2019.
-
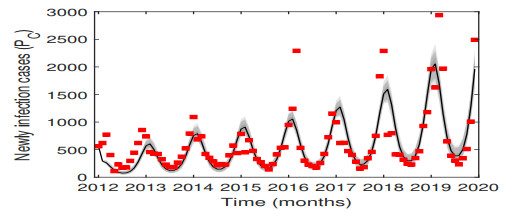
Figure 3. It presents the fitting outcomes of influenza cases, in which the red dot indicates the actual number of infection individuals, the black line indicates the fitted cases, and the gray area from the brightest to the darkest indicates the 50
$ \% $ , 90$ \% $ , 95$ \% $ , and 99$ \% $ posterior limits of the system. -
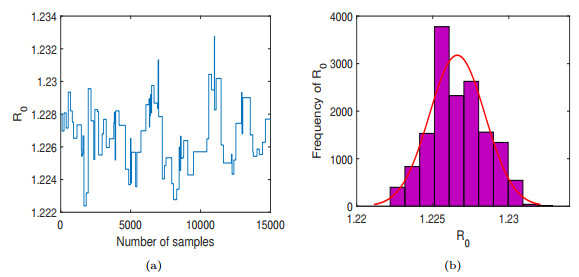
Figure 4. (a) The Markov chain samples of
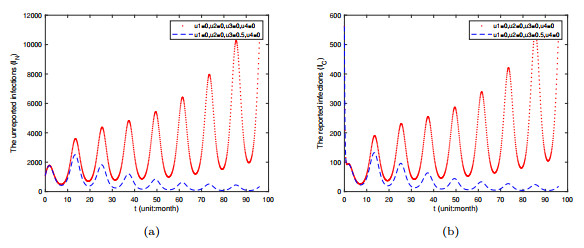
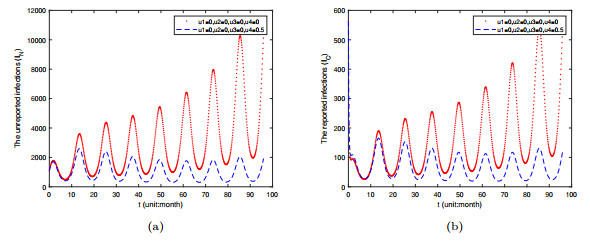
$ R_{0} $ . (b) The distribution of$ R_{0} $ is derived by the Markov Chain Monte Carlo (MCMC) algorithm. The vermilion line is the probability density function of$ R_{0} $ . - Figure 5. Time varying plots of reported infected individuals and unreported infected individuals under the implementation of one control measure u3.
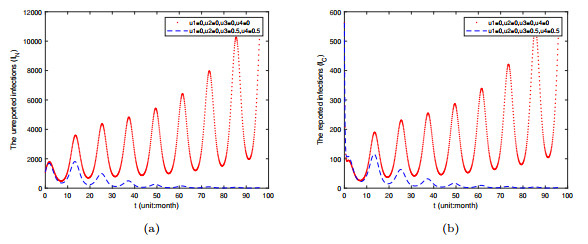
- Figure 6. Time varying plots of reported infected individuals and unreported infected individuals under the implementation of one control measure u4.
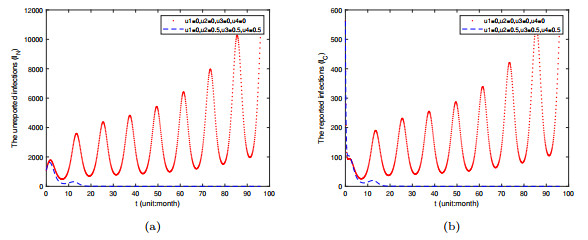
- Figure 7. Time varying plots of reported infected individuals and unreported infected individuals under the implementation of two control measures u3 and u4.
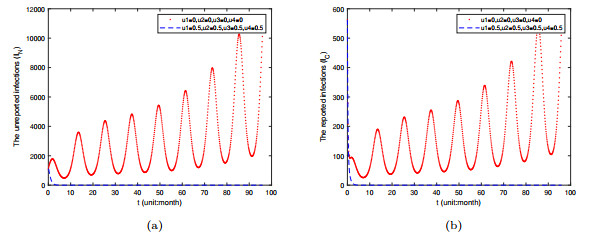
- Figure 8. Time varying plots of reported infected individuals and unreported infected individuals under the implementation of three control measures u2, u3 and u4.
- Figure 9. Time varying plots of reported infected individuals and unreported infected individuals under the implementation of four control measures u1, u2, u3 and u4.
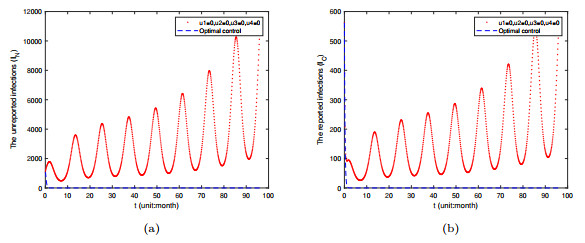
- Figure 10. Time varying plots of reported infected individuals and unreported infected individuals under the implementation of the optimal control measures.
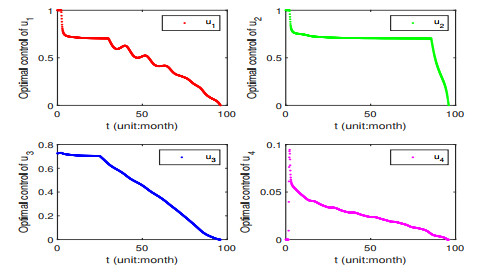
- Figure 11. The optimal control variables ui (i=1, 2, 3, 4) of the optimal control measures.
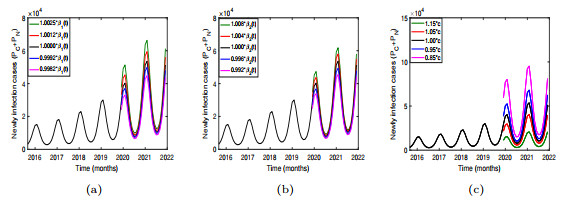
- Figure 12. (a) indicates that the change of contact rate function β1(t) has an impact on the size of new cases. (b) indicates that the change of contact rate function β2(t) has an impact on the size of new cases. (c) The impact of vaccination rate c on the size of new cases.
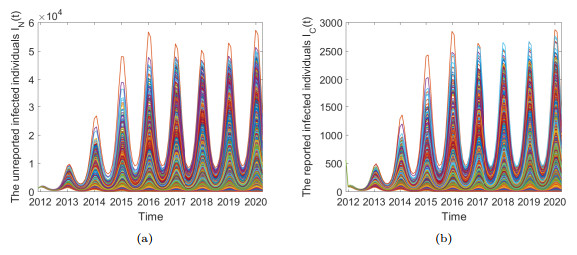
- Figure 13. (a) The system (2.1) outputs the results of 2000 runs, the abscissa represents the variable IN (t), the ordinate represents the time (months). (b)The system (2.1) outputs the results of 2000 runs, the abscissa represents the variable IC (t), the ordinate represents the time (months)
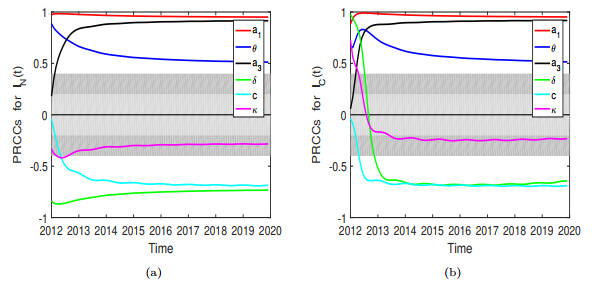
- Figure 14. (a) The effect of parameter sensitivity changes over time on unreported infected individuals (IN (t)). (b) The effect of parameter sensitivity changes over time on unreported infected individuals (IC (t)).
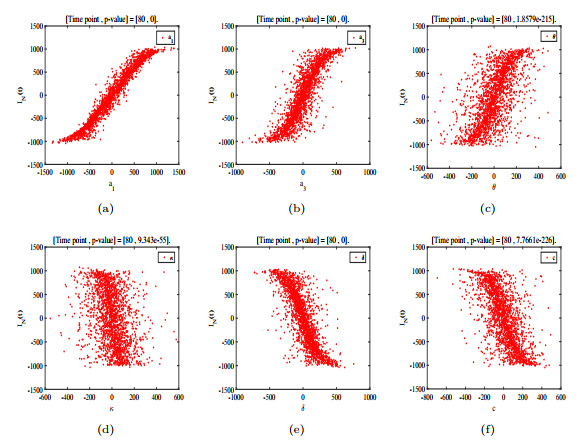
- Figure 15. The p-value of each parameter of IN (t) at the 80th month.
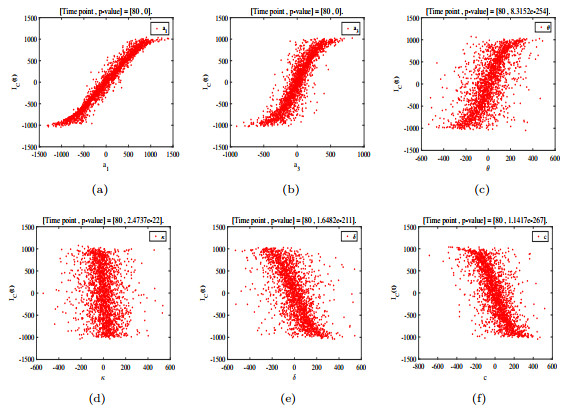
- Figure 16. The p-value of each parameter of IC (t) at the 80th month.
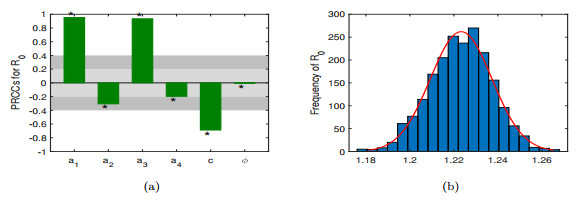
- Figure 17. (a) The PRCCs of the basic reproduction number R0 in the system (2.1). (b) The 2000 samples of R0 is derived by the Latin hypercube sampling. (c) The distribution of R0 is derived by the Latin hypercube sampling.
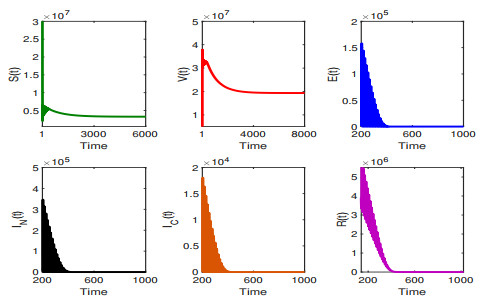
- Figure 18. Numerical simulation will be used to verify some theoretical results of the system (2.1). This figure means that when R0 is less than unity, the influenza will eventually die.
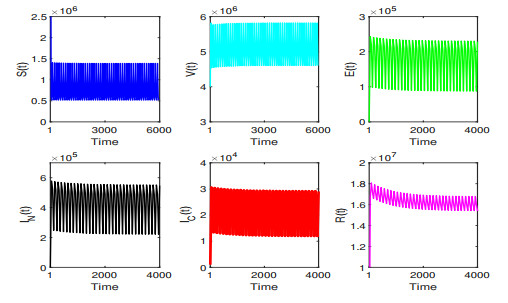
- Figure 19. Numerical simulation will be used to verify some theoretical results of the system (2.1). This figure means that when R0 is greater than unity, the influenza will always exist.