| Citation: | Houfu Liu, Yuanyuan Cong, Ying Su. DYNAMICS OF A TWO-PATCH NICHOLSON'S BLOWFLIES MODEL WITH RANDOM DISPERSAL[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 692-711. doi: 10.11948/20210268 |
DYNAMICS OF A TWO-PATCH NICHOLSON'S BLOWFLIES MODEL WITH RANDOM DISPERSAL
-
Abstract
The global dynamics of the Nicholson's blowfly reaction-diffusion model with zero Dirichlet boundary condition is less understood. In this paper, we provide a discrete version of diffusive Nichlson's blowflies equation with zero Dirichlet boundary condition. Local and global stability of the equilibria are obtained by some comparison arguments, fluctuation method and the theory of exponential ordering. Hopf bifurcation at the positive equilibrium and the global existence of the periodic solutions are studied by local and global Hopf bifurcation theory.
-

-
References
[1] K. A. G. Azevedo and L. A. C. Laderira, Hopf bifurcation for a class of partial differnetial equation with delay, Funkcialaj Ekvacioj, 2004, 47, 395-422. doi: 10.1619/fesi.47.395 [2] L. Berezansky, E. Braverman and L. Idels, Nicholson's blowflies differential equations revisited: main results and open problems, Appl. Math. Model, 2010, 34, 1405-1417. doi: 10.1016/j.apm.2009.08.027 [3] S. Busenberg and W. Huang, Stability and Hopf bifurcation for a population delay model with diffusion effects, J. Differerential Equations, 1996, 124(1), 80-107. doi: 10.1006/jdeq.1996.0003 [4] S. Chen, Y. Lou and J. Wei, Hopf bifurcation in a delayed reaction-diffusion-advection population model, J. Differerential Equations, 2018, 264, 5333-5359. doi: 10.1016/j.jde.2018.01.008 [5] S. Chen and J. Shi, Stability and Hopf bifurcation in a diffusive logistic population model with nonlocal delay effect, J. Differential Equations, 2012, 253(12), 3440-3470. doi: 10.1016/j.jde.2012.08.031 [6] S. Chen and J. Yu, Stability and bifurcations in a nonlocal delayed reaction-diffusion population model, J. Differential Equations, 2016, 260(1), 218-240. doi: 10.1016/j.jde.2015.08.038 [7] S. Guo, Stability and bifurcation in a reaction-diffusion model with nonlocal delay effect, J. Differential Equations, 2015, 259(4), 1409-1448. doi: 10.1016/j.jde.2015.03.006 [8] S. Guo and S. Yan, Hopf bifurcation in a diffusive Lotka-Volterra type system with nonlocal delay effect, J. Differential Equations, 2016, 260(1), 781-817. doi: 10.1016/j.jde.2015.09.031 [9] M. S. Gurney, S. P Blythe and R. M. Nisbet, Nicholson's bowflies revisited, Nature, 1980, 287, 17-21. doi: 10.1038/287017a0 [10] B. Hassard, N. Kazarinoff and Y. Wan, Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge, 1981. [11] Z. Jin and R. Yuan, Hopf bifurcation in a reaction-diffusion-advection equation with nonlocal delay effect, J. Differerential Equations, 2021, 271(1), 533-562. [12] J. Li, Global attractivity in Nicholson's blowflies, Applied Mathematics, 1996, 11(4), 425-434. doi: 10.1007/BF02662882 [13] K. Liao and Y. Lou, The effect of time delay in a two-patch model with random dispersal, Bull. Math. Biol., 2014, 76, 335-376. doi: 10.1007/s11538-013-9921-7 [14] Z. Ma, H. Huo and H. Xiang, Hopf bifurcation for a delyed predator-prey diffusion system with Dirichlet boundary condition, Applied Mathematics and Computation, 2017, 311, 1-18. [15] A. J. Nicholson, Compensatory reactions of populations to stresses, and their evolutionary significance, Australian Journal of Zoology, 1954, 2, 1-8. doi: 10.1071/ZO9540001 [16] S. Ruan and J. Wei, On the zeros of transcendental functions with applications to stability of delay differential equations with two delays, Dynam. Contin. Discrete Impulsive Syst. Ser. A Math. Anal., 2003, 10, 863-874. [17] H. L. Smith, Monotone Dynamical Systems: An introduction to the theory of competitive and cooperative systems, American Mathematical Society, Providence, Rhode Island, 2008. [18] H. L. Smith and H. Thieme, Strongly order preserving semiflows generated by functional differential equations, J. Differential Equations, 1991, 93, 332-363. doi: 10.1016/0022-0396(91)90016-3 [19] J. W. H. So, J. Wu and Y. Yang, Numerical steady-state and Hopf bifurcation analysis on the diffusive Nicholson's blowflies equation, Appl. Math. Comput., 2000, 111, 33-51. [20] J. W. H. So and Y. Yang, Dirichlet problem for the diffusive Nicholson's blowflies equation, J. Differential Equations, 1998, 150(2), 317-348. doi: 10.1006/jdeq.1998.3489 [21] Y. Su, J. Wei and J. Shi, Hopf bifurcations in a reaction?Cdiffusion population model with delay effect, J. Differential Equations, 2009, 247(4), 1156-1184. doi: 10.1016/j.jde.2009.04.017 [22] Y. Su, J. Wei and J. Shi, Hopf bifurcation in a diffusive logistic equation with mixed delayed and instantaneous density dependence, J. Dynam. Differential Equations, 2012, 24(4), 897-925. doi: 10.1007/s10884-012-9268-z [23] J. Wei and M. Li, Hopf bifurcation analysis in a delayde Nicholson's blowflies equation, Nonlinear Anal. TMA, 2005, 60, 1351-1367. doi: 10.1016/j.na.2003.04.002 [24] J. Wu, Symmetric functional differential equations and neural networks with memory, Trans. Amer. Math. Soc., 1998, 350, 4799-4838. doi: 10.1090/S0002-9947-98-02083-2 [25] X. Yan and W. Li, Stability of bifurcating periodic solutions in a delayed reaction?Cdiffusion population model, Nonlinearity, 2010, 23(6), 1413-1431. doi: 10.1088/0951-7715/23/6/008 [26] X. Yan and W. Li, Stability and Hopf bifurcations for a delayed diffusion system in population dynamics, Discrete Contin. Dyn. Syst. Ser. B, 2012, 17(1), 367-399. [27] Y. Yang and J. W. H. So, Dynamics of the diffusive Nicholson's blowflies equation. in: Wenxiong Chen, Shouchuan Hu. (Eds.), in: Proceedings of the International Conference on Dynamical Systems and Differential Equations, Vol. Ⅱ, Springfield, Missouri, U.S. A, 1996, An added volume to Discrete Contin. Dyn. Syst., 1998, 333-352. [28] T. Yi, Y Chen and J. Wu, Threshold dynamics of a delayed reaction diffusion equation subject to the Dirichlet condition, J. Biol. Dyn., 2009, 3, 331-341. doi: 10.1080/17513750802425656 [29] X. Zhang, S. Song and J. Wu, Onset and termination of oscillation of disease spread through contaminated environment, Mathematical Biosciences and Engineering, 2017, 14(5/6), 1515-1533. doi: 10.3934/mbe.2017079 [30] X. Zhao, Global attractivity in a class of non-monotone reaction-diffusion equations with time delay, Cand. Appl. Math. Quart., 2009, 17(1), 271-281. [31] L. Zhou, Y. Tang and S. Hussein, Stability and Hopf bifurcation for a delay competition diffusion system, Chaos, Solution and Fractals, 2002, 14, 1201-1225. doi: 10.1016/S0960-0779(02)00068-1 -
-
-
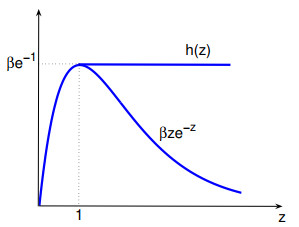
Figure 1. Function
$ h(z) $




 DownLoad:
DownLoad: