| Citation: | Minzhi Wei, Zizun Li. EXISTENCE OF KINK WAVES TO PERTURBED DISPERSIVE K(3, 1) EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 712-719. doi: 10.11948/20210293 |
EXISTENCE OF KINK WAVES TO PERTURBED DISPERSIVE K(3, 1) EQUATION
-
Abstract
This paper concerns on the existence problem of traveling wave solutions to perturbed dispersive K(3, 1) equation by using geometric singular perturbation technique. Based on the analogy between solitary wave solutions and heteroclinic orbits of the associated ordinary differential equations, kink and antikink waves persistent is concluded when the perturbed parameter is small sufficiently in perturbed nonlinear wave equation.
-

-
References
[1] A. Chen, L. Guo and X. Deng, Existence of solitary waves and periodic waves for a perturbed generalized BBM equation, J. Diff. Equat., 2016, 261, 5324-5349. doi: 10.1016/j.jde.2016.08.003 [2] C. Cheng and T. Kš1pper, Dynamical behavior of two-soliton solution exhibited by perturbed sine-Gordon equation. Math. Nachr., 1995, 171, 53šC77. [3] T. Cosgun and M. Sari, Traveling wave solutions and stability behaviours under advection dominance for singularly perturbed advection-diffusion-reaction processes, Chaos, Solitons & Fractals, 2020, 138, 109881. [4] P. T. Dinda and M. Remoissenet, Breather compactons in nonlinear Klein-Gordon systems, Phys. Rev. E, 1999, 60, 6218-6221. doi: 10.1103/PhysRevE.60.6218 [5] Z. Du and Q. Qiao, The dynamics of traveling waves for a nonlinear Belousov-Zhabotinskii system, J. Diff. Equat., 2020, 269, 7214-7230. doi: 10.1016/j.jde.2020.05.033 [6] Z. Du, J. Liu and Y. Ren, Traveling pulse solutions of a generalized Keller-Segel system with small cell diffusion via a geometric approach, J. Diff. Equat., 2021, 270, 1019-1042. doi: 10.1016/j.jde.2020.09.009 [7] N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, J. Differ. Equat., 1979, 31, 53-98. doi: 10.1016/0022-0396(79)90152-9 [8] A. Ghazaryan, S. Lafortune and C. Linhart, Flame propagation in a porous medium, Physica D, 2020, 413, 132653. doi: 10.1016/j.physd.2020.132653 [9] J. Ge and Z. Du, The solitary wave solutions of the nonlinear perturbed shallow water wave model, Appl. Math. Lett., 2020, 103, 106202. doi: 10.1016/j.aml.2019.106202 [10] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical System, and Bifurcation of Vector Fields, Springer Verlag, New York, 1983. [11] M. Han, Bifurcation Theory and Periodical Solution of Dynamic System, Beijing: Science Press, 2002. [12] C. K. R. T. Jones., Geometric singular perturbation theory. Lecture Notes Math, Springer-Verlag, 1994, 1609, 45-118. [13] Y. Kivshar, Compactons in discrete lattices, Nonlinear Coherent Struct, Phys. Biol., 1994, 329, 255-258. [14] J. Li and H. Dai, On the Study of Singular Nonlinear Travelling Wave Equations: Dynamical Approach, Science Press, Beijing, 2007. [15] X. Li, Z. Du and S. Ji, Existence results of solitary wave solutions for a delayed Camassa-Holm-KP equation, Commun. Pure & Appl. Ana., 2019, 18, 2961-2981. [16] M. B. A. Mansour, A geometric construction of traveling waves in a generalized nonlinear dispersive-dissipative equation, J. Geom. Phys., 2013, 69, 116-122. doi: 10.1016/j.geomphys.2013.03.004 [17] L. Perko, Differential Equations and Dynamical Systems, New York: Springer Science & Business Media, 2013. [18] P. Rosenau and J. M. Hyman, Compactons: solitons with finite wavelength, Phys. Rev. Lett., 1993, 70, 564-567. doi: 10.1103/PhysRevLett.70.564 [19] P. Rosenau, On nonanalytic solitary waves formed by a nonlinear dispersion, Phys. Lett. A, 1997, 230, 305-318. doi: 10.1016/S0375-9601(97)00241-7 [20] Z. Wen, On existence of kink and antikink wave solutions of singularly perturbed Gardner equation, Math. Meth. Appl. Sci., 2020, 1-6. [21] X. Wu, W. Rui and X. Hong, Exact traveling wave solutions of explicit type, implicit type, and parametric type for K(m, n) equation, J. Appl. Math., 2012, 236875. [22] W. Yan, Z. Liu and Y. Liang, Existence of solitary waves and periodic waves to a perturbed generalized KdV equation, Math. Model. Anal., 2014, 19, 537-555. doi: 10.3846/13926292.2014.960016 -
-
-
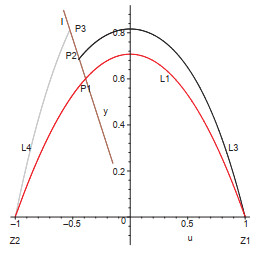
Figure 1. Heteroclinic orbits of system (3.5)) under the condition
$ c<0, \ \sigma<0 $ . -
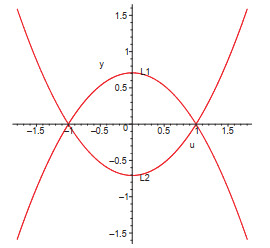
Figure 2. Diagram of the connection of saddles of system (3.8) with
$ 0<\varepsilon\ll1 $ . -
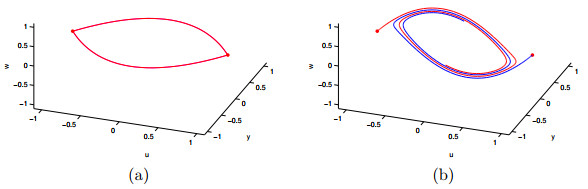
Figure 3. Simulations: (a) shows the existence of heteroclinic orbits of system (3.2) for
$ \varepsilon=0.01 $ , (b) shows the heteroclinic orbits blow up for$ \varepsilon=0.1 $ .




 DownLoad:
DownLoad: