| Citation: |
Hui Wu, Yafei Zhao, Chen Zhang, Jianhong Wu, Jie Lou. STRUCTURAL AND PRACTICAL IDENTIFIABILITY ANALYSES ON THE TRANSMISSION DYNAMICS OF COVID-19 IN THE UNITED STATES[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1475-1495. doi: 10.11948/20210300
|
STRUCTURAL AND PRACTICAL IDENTIFIABILITY ANALYSES ON THE TRANSMISSION DYNAMICS OF COVID-19 IN THE UNITED STATES
-
Abstract
We formulate an epidemic model to capture essential epidemiology of COVID-19 and major public health interventions. We start with a system of differential equations involving six compartments, and we use the Goodman and Weare affine invariant ensemble Markov Chain Monte Carlo algorithm (GWMCMC) to identify a simplified version of the full model that consists of only four compartments. We examine well-posedness of the relevant parameter estimation problem for the given observations using the U.S. epidemic data; study the reliability of model selection; analyze the structural identifiability of the selected model; and conduct a practical identifiability analysis on the selected model using the GWMCMC algorithm. Our study shows that the selected model is structurally identifiable for the confirmed cases, and for small measurement errors, key parameters such as the transmission rate are practically identifiable. We also analyze the stability of the selected model and prove the global asymptotic stability of the disease-free equilibrium and the endemic equilibrium by constructing appropriate Lyapunov functions. Our numerical experiments show that the U.S. will undergo damped transit oscillations towards the endemicity.
-
Keywords:
- Dynamic model /
- COVID-19 /
- model selection /
- identifiability analysis
-
-
References
[1] H. Akaike, Information theory and an extension of the maximum likelihood principle, in Selected papers of hirotugu akaike, Springer, 1998, 199–213. [2] G. Bellu, M. P. Saccomani, S. Audoly and L. D'Angiò, Daisy: A new software tool to test global identifiability of biological and physiological systems, Computer methods and programs in biomedicine, 2007, 88(1), 52–61. doi: 10.1016/j.cmpb.2007.07.002 [3] X. Chang, M. Liu, Z. Jin and J. Wang, Studying on the impact of media coverage on the spread of covid-19 in hubei province, China, Math. Biosci. Eng., 2020, 17(4), 3147–3159. doi: 10.3934/mbe.2020178 [4] T. Chen, J. Rui, Q. Wang et al., A mathematical model for simulating the phase-based transmissibility of a novel coronavirus, Infectious diseases of poverty, 2020, 9(1), 1–8. doi: 10.1186/s40249-019-0617-6 [5] O. T. Chis, J. R. Banga and E. Balsa-Canto, Structural identifiability of systems biology models: a critical comparison of methods, PloS one, 2011, 6(11), e27755. doi: 10.1371/journal.pone.0027755 [6] O. Diekmann, J. A. P. Heesterbeek and J. A. Metz, On the definition and the computation of the basic reproduction ratio r 0 in models for infectious diseases in heterogeneous populations, Journal of mathematical biology, 1990, 28(4), 365–382. [7] Daily data on covid-19. https://voice.baidu.com/act/newpneumonia/newpneumonia/?from=osari_aladin_banner#tab4. [8] M. C. Eisenberg, S. L. Robertson and J. H. Tien, Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease, Journal of theoretical biology, 2013, 324, 84–102. doi: 10.1016/j.jtbi.2012.12.021 [9] N. M. Ferguson, D. Laydon, G. Nedjati-Gilani et al., Impact of non-pharmaceutical interventions (npis) to reduce Covid-19 mortality and healthcare demand, 2020. [10] M. Gatto, E. Bertuzzo, L. Mari et al., Spread and dynamics of the Covid-19 epidemic in Italy: Effects of emergency containment measures, Proceedings of the National Academy of Sciences, 2020, 117(19), 10484–10491. doi: 10.1073/pnas.2004978117 [11] G. Giordano, F. Blanchini, R. Bruno et al., Modelling the covid-19 epidemic and implementation of population-wide interventions in Italy, Nature medicine, 2020, 26(6), 855–860. doi: 10.1038/s41591-020-0883-7 [12] J. Goodman and J. Weare, Ensemble samplers with affine invariance, Communications in applied mathematics and computational science, 2010, 5(1), 65–80. [13] J. Guedj, R. Thiébaut and D. Commenges, Practical identifiability of HIV dynamics models, Bulletin of mathematical biology, 2007, 69(8), 2493–2513. doi: 10.1007/s11538-007-9228-7 [14] Z. He, L. Ren, J. Yang et al., Seroprevalence and humoral immune durability of Anti-Sars-Cov-2 antibodies in wuhan, China: a longitudinal, population-level, cross-sectional study, The Lancet, 2021, 397(10279), 1075–1084. doi: 10.1016/S0140-6736(21)00238-5 [15] J. P. La Salle, The stability of dynamical systems, SIAM, 1976. [16] M. Li, G. Sun, J. Zhang et al., Analysis of Covid-19 transmission in Shanxi province with discrete time imported cases, Math. Biosci. Eng., 2020, 17(4), 3710. doi: 10.3934/mbe.2020208 [17] Q. Li, X. Guan, P. Wu et al., Early transmission dynamics in Wuhan, china, of novel coronavirus–infected pneumonia, New England journal of medicine, 2020. [18] Q. Li, B. Tang, J. Wu et al., Mathematical model reveals the influence of execution and adherence of mitigation strategies on the later period of Covid-19 and resumption of work, Journal of Shaanxi Normal University (Natural Science Edition), 2020, 48(3), 1–6. [19] P. Liu, S. He, L. Rong and S. Tang, The effect of control measures on Covid-19 transmission in Italy: Comparison with guangdong province in china, Infectious Diseases of Poverty, 2020, 9(1), 1–13. doi: 10.1186/s40249-019-0617-6 [20] D. P. Lizarralde-Bejarano, D. Rojas-Díaz, S. Arboleda-Sánchez and M. E. Puerta-Yepes, Sensitivity, uncertainty and identifiability analyses to define a dengue transmission model with real data of an endemic municipality of Colombia, PloS one, 2020, 15(3), e0229668. doi: 10.1371/journal.pone.0229668 [21] H. Miao, C. Dykes, L. M. Demeter and H. Wu, Differential equation modeling of HIV viral fitness experiments: model identification, model selection, and multimodel inference, Biometrics, 2009, 65(1), 292–300. doi: 10.1111/j.1541-0420.2008.01059.x [22] H. Miao, X. Xia, A. S. Perelson and H. Wu, On identifiability of nonlinear ode models and applications in viral dynamics, SIAM review, 2011, 53(1), 3–39. doi: 10.1137/090757009 [23] W. C. Roda, Bayesian inference for dynamical systems, Infectious Disease Modelling, 2020, 5, 221–232. doi: 10.1016/j.idm.2019.12.007 [24] W. C. Roda, M. B. Varughese, D. Han and M. Li, Why is it difficult to accurately predict the Covid-19 epidemic?, Infectious disease modelling, 2020, 5, 271–281. doi: 10.1016/j.idm.2020.03.001 [25] G. Schwarz, Estimating the dimension of a model, The annals of statistics, 1978, 461–464. [26] N. Sugiura, Further analysts of the data by Akaike's information criterion and the finite corrections: Further analysts of the data by Akaike's, Communications in Statistics-theory and Methods, 1978, 7(1), 13–26. doi: 10.1080/03610927808827599 [27] H. B. Taboe, K. V. Salako, J. M. Tison et al., Predicting Covid-19 spread in the face of control measures in west Africa, Mathematical biosciences, 2020, 328, 108431. [28] B. Tang, X. Wang, Q. Li et al., Estimation of the transmission risk of the 2019-ncov and its implication for public health interventions, Journal of clinical medicine, 2020, 9(2), 462. doi: 10.3390/jcm9020462 [29] N. Tuncer, H. Gulbudak, V. L. Cannataro and M. Martcheva, Structural and practical identifiability issues of immuno-epidemiological vector–host models with application to rift valley fever, Bulletin of mathematical biology, 2016, 78(9), 1796–1827. doi: 10.1007/s11538-016-0200-2 [30] N. Tuncer and T. T. Le, Structural and practical identifiability analysis of outbreak models, Mathematical biosciences, 2018, 299, 1–18. doi: 10.1016/j.mbs.2018.02.004 [31] N. Tuncer, C. Mohanakumar, S. Swanson and M. Martcheva, Efficacy of control measures in the control of ebola, Liberia 2014–2015, Journal of biological dynamics, 2018, 12(1), 913–937. doi: 10.1080/17513758.2018.1535095 [32] The average life expectancy of individual. https://www.cia.gov. [33] H. Wu, H. Miao, H. Xue et al., Quantifying immune response to influenza virus infection via multivariate nonlinear ode models with partially observed state variables and time-varying parameters, Statistics in Biosciences, 2015, 7(1), 147–166. doi: 10.1007/s12561-014-9108-2 [34] Weikun, A parallel implementation of mcmc. [35] W. Xia, T. Sanyi, C. Yong et al., When will be the resumption of work in Wuhan and its surrounding areas during Covid-19 epidemic? A data-driven network modeling analysis, Scientia Sinica Mathematica, 2020. -
-
Figures(6) / Tables(7)
Export File
Citation
Hui Wu, Yafei Zhao, Chen Zhang, Jianhong Wu, Jie Lou. STRUCTURAL AND PRACTICAL IDENTIFIABILITY ANALYSES ON THE TRANSMISSION DYNAMICS OF COVID-19 IN THE UNITED STATES[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1475-1495. doi: 10.11948/20210300
Format
Content
DownLoad:
-
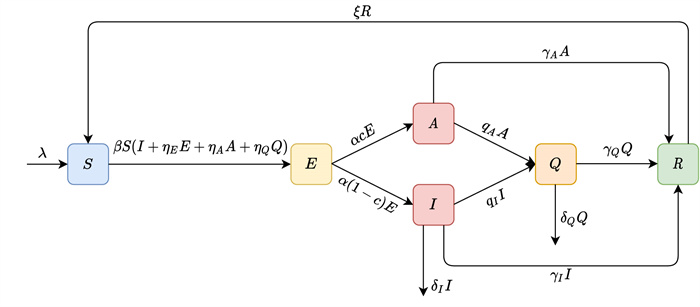
Figure 1. The compartment diagram of the full-model.
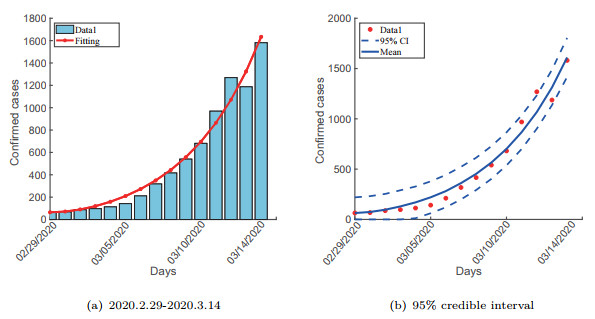
$ \lambda $ is the constant recruitment rate;$ \beta $ is the transmission rate of$ I $ compartment;$ \eta_{i} , i=E, A, Q $ are the multiple of the transmission rate of$ E $ ,$ A $ and$ Q $ compartment relative to$ I $ compartment respectively;$ c $ is the proportion of asymptomatic infection;$ \gamma_{i}, i=A, I, Q $ represent the recovery rate of$ A $ ,$ I $ and$ Q $ compartment respectively;$ \delta_{i}, i=I, Q $ represent the disease-induced death rate of$ I $ and$ Q $ compartment respectively;$ \frac{1}{\alpha} $ is the incubation period;$ q_{i}, i=A, I $ represent the detection rate of$ A $ and$ I $ compartment respectively;$ \xi $ is the rate of the recovered patients return to the susceptible population due to the weakening or disappearance of antibodies;$ \omega $ is the natural mortality rate which is not shown in the figure. - Figure 2. Fitting results. (a) Fitting of Model 4 to the data of COVID-19 in the United States from February 29 to March 14, 2020. (b) It's 95% confidence interval.
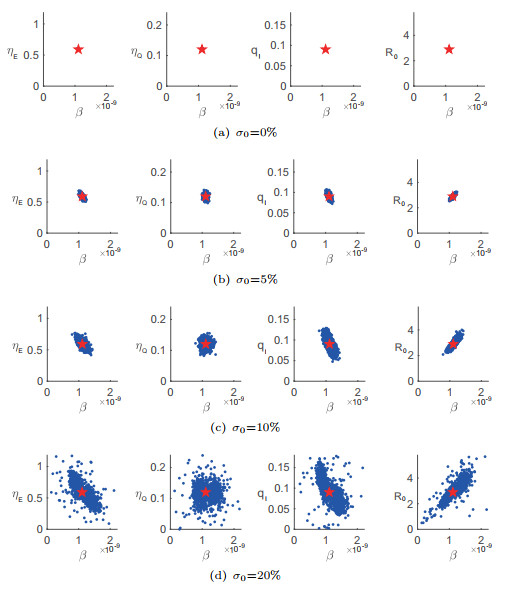
- Figure 3. The parameter estimates of the Model 4 for 1000 synthetic data generated by Gaussian noise. True parameters are indicated by red stars.
-
Figure 4. The frequency distribution histograms of
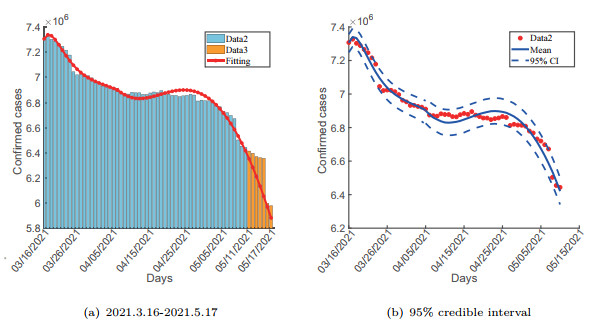
$ {\cal R}_{0} $ from 1000 simulations for measurement error levels$ \sigma_{0}=10\% $ and$ \sigma_{0}=20\% $ . - Figure 5. Fitting results. (a)Piecewise fit of the model (4.1) to the data of COVID-19 in the United States from March 15 to May 10, 2021. (b)95% confidence interval.
-
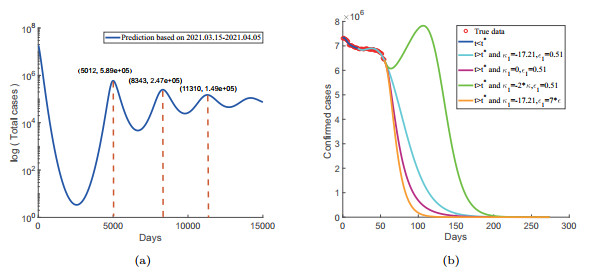
Figure 6. Prediction in different situations.(a) The prediction of total cases with
$ \kappa=11.24, \epsilon=0.12 $ and$ t<t^{*} $ . (b) The prediction of the number of confirmed cases with different values of$ \kappa_1 $ and$ \epsilon_1 $ .