| Citation: |
Yaxiang Li, Jiangxing Wang. HIGH ORDER PARAMETER-UNIFORM CONVERGENT HDG METHOD FOR SINGULARLY PERTURBED CONVECTION-DIFFUSION PROBLEM[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1466-1474. doi: 10.11948/20210283
|
HIGH ORDER PARAMETER-UNIFORM CONVERGENT HDG METHOD FOR SINGULARLY PERTURBED CONVECTION-DIFFUSION PROBLEM
-
Abstract
In this paper, a high order hybridizable discontinuous Galerkin method (HDG) on two layer-adapted meshes have been developed for the singularly perturbed convection-diffusion problems in one and two-dimensional. The existence and uniqueness of the HDG solutions are verified. Thanks to the implementation of two-type different anisotropic meshes, i.e., the Shishkin and an improved grade meshes, the uniform 2k + 1 -order super-convergence is obtained for both one-dimensional and two-dimensional cases.
-
-
References
[1] R. Bustinza, A. Lombardi and M. Solano, An anisotropic a priori error analysis for a convection-dominated diffusion problem using the HDG method, Comput. Methods Appl. Mech. Engin., 2019, 345, 382–491. doi: 10.1016/j.cma.2018.11.010 [2] B. Cockburn, J. Gopalakrishna and R. Lazarov, Unified hybridization of discontinuous {G}alerkin, mixed, and continuous galerkin methods for second order elliptic problems, SIAM J. Numer. Anal., 2009, 47(2), 1319–1365. doi: 10.1137/070706616 [3] B. Cockburn, J. Gopalakrishnan and F. Sayas, A projection-based error analysis of hdg methods, Math. Comput., 2010, 79, 1351–1367. doi: 10.1090/S0025-5718-10-02334-3 [4] B. Cockburn and J. Shen, A hybridizable discontinuous galerkin method for the p-laplacian, SIAM J. Sci. Comput., 2016, 38(1), A545–A566. doi: 10.1137/15M1008014 [5] S. Du and F. Sayas, A unified error analysis of hybridizable discontinuous Galerkin methods for the static maxwell equations, SIAM J. Numer. Anal., 2020, 58(2), 1367–1391. doi: 10.1137/19M1290966 [6] P. Fernandez, A. Christophe, S. Terrana et al., Hybridized discontinuous galerkin methods for wave propagation, J. Sci. Comput., 2018, 77(3), 1566–1604. doi: 10.1007/s10915-018-0811-x [7] G. Fu, W. Qiu and W. Zhang, An analysis of HDG methods for convection-dominated diffusion problems, ESAIM: Math. Model. Numer. Anal., 2015, 49(1), 225–256. doi: 10.1051/m2an/2014032 [8] M. Giacomini, R. Sevilla and A. Huerta, Tutorial on hybridizable discontinuous galerkin (HDG) formulation for incompressible flow problems, in Modeling in Engineering Using Innovative Numerical Methods for Solids and Fluids, Springer, 2020, 163–201. [9] V. Kučera, On diffusion-uniform error estimates for the DG method applied to singularly perturbed problems, IMA J. Numer. Anal, 2014, 34(2), 820–861. doi: 10.1093/imanum/drt007 [10] R. Lin, X. Ye, S. Zhang and P. Zhu, A weak Galerkin finite element method for singularly perturbed convection-diffusion–reaction problems, SIAM J. Numer. Anal., 2018, 56(3), 1482–1497. doi: 10.1137/17M1152528 [11] Z. Liu and J. Zhang, Analysis of the SDFEM in a streamline diffusion norm for singularly perturbed convection diffusion problems, Appl. Math. Let., 2017, 69, 61–66. doi: 10.1016/j.aml.2017.02.005 [12] W. Qiu and K. Shi, An HDG method for convection diffusion equation, J. Sci. Comput., 2016, 66(1), 346–357. doi: 10.1007/s10915-015-0024-5 [13] H. Roos, M. Stynes and L. Tobiska, Robust numerical methods for singularly perturbed differential equations: convection-diffusion-reaction and flow problems, 24, Springer Science & Business Media, 2008. [14] H. Roos and H. Zarin, The discontinuous Galerkin method for singularly perturbed problems, in Numerical Mathematics and Advanced Applications, Springer, 2004, 736–745. [15] A. L. Spina, M. Kronbichler, M. Giacomini et al., A weakly compressible hybridizable discontinuous Galerkin formulation for fluid–structure interaction problems, Comput. Methods Appl. Mech. and Engin., 2020, 372, 113392. doi: 10.1016/j.cma.2020.113392 [16] H. Tian, Z. Zhang and Z. Zhu, Convergence analysis of the LDG method for singularly perturbed two-point boundary value problems, Commun. Math. Sci., 2011, 9(4), 1013–1032. doi: 10.4310/CMS.2011.v9.n4.a4 [17] Z. Xie and Z. Zhang, Superconvergence of dg method for one-dimensional singularly perturbed problems, J. Computat. Math., 2007, 185–200. [18] Z. Xie and Z. Zhang, Uniform superconvergence analysis of the discontinuous galerkin method for a singularly perturbed problem in 1-D, Math. Comput., 2010, 79(269), 35–45. doi: 10.1090/S0025-5718-09-02297-2 [19] Z. Xie, Z. Zhang and Z. Zhang, A numerical study of uniform superconvergence of ldg method for solving singularly perturbed problems, J. Comput. Math., 2009, 280–298. [20] H. Zhu and Z. Zhang, Convergence analysis of the LDG method applied to singularly perturbed problems, Numerical Methods for Partial Differential Equations, 2013, 29(2), 396–421. doi: 10.1002/num.21711 [21] H. Zhu and Z. Zhang, Uniform convergence of the LDG method for a singularly perturbed problem with the exponential boundary layer, Math. Comput., 2014, 83(286), 635–663. -
-
Figures(2) / Tables(5)
Export File
Citation
Yaxiang Li, Jiangxing Wang. HIGH ORDER PARAMETER-UNIFORM CONVERGENT HDG METHOD FOR SINGULARLY PERTURBED CONVECTION-DIFFUSION PROBLEM[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1466-1474. doi: 10.11948/20210283
Format
Content
DownLoad:
-
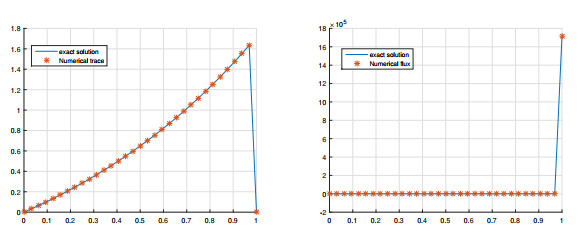
Figure 1.
$ u $ and$ \hat{u}_h $ (left),$ q $ and$ \hat{q}_h $ (right) under uniform mesh,$ N=32, k=1, \epsilon=10^{-6} $ . -
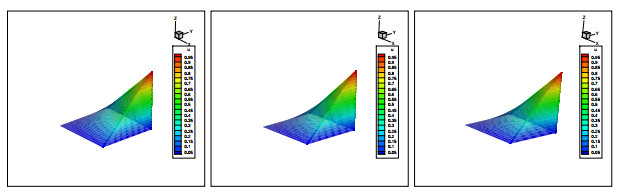
Figure 2. From left to right: exact solution, Numerical solution
$ k=2, $ and Numerical solution$ k=3 $ for$ \epsilon=1.0e-6 $