| Citation: |
Feng Zhang, Yuru Hu, Xiangpeng Xin, Hanze Liu. DARBOUX TRANSFORMATION, EXACT SOLUTIONS OF THE VARIABLE COEFFICIENT NONLOCAL FOKAS-LENELLS EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1544-1557. doi: 10.11948/20210328
|
DARBOUX TRANSFORMATION, EXACT SOLUTIONS OF THE VARIABLE COEFFICIENT NONLOCAL FOKAS-LENELLS EQUATION
-
Abstract
In this paper, a (1+1)-dimensional integrable variable coefficient nonlocal Fokas-Lenells (NFL) equation is studied. On the basis of the Lax pair, the Darboux transformation of the variable coefficient NFL equation is constructed at the first time and an explicit form of the N-fold Darboux transformation is given. The exact solutions of the variable coefficient NFL equation are derived using the zero seed solution and the nonzero seed solution according to the Darboux transformation. Subsequently, one-soliton solution, two-soliton solution, and kink solution with periodic waves are obtained by choosing the proper parameters and plotting the corresponding figures. With the help of figures, the behaviors of the obtained solutions are revealed and it is possible to find that the interaction between solitons is elastic no matter the coefficient function is constant or arbitrary variable. In addition, this paper also indicates that the exact solutions of the variable coefficient NFL equation are more general than its constant coefficient form.
-
Keywords:
- Lax pair /
- soliton solutions /
- nonlocal equation /
- Darboux transformation method
-
-
References
[1] M. J. Ablowitz and Z. H. Musslimani, Integrable nonlocal nonlinear Schrödinger equation, Physical Review Letters, 2013, 110, 064105. doi: 10.1103/PhysRevLett.110.064105 [2] Z. Chai, D. Sun, H. Wang and B. Shi, A comparative study of local and nonlocal Allen-Cahn equations with mass conservation, International Journal of Heat and Mass Transfer, 2018, 122, 631–642. doi: 10.1016/j.ijheatmasstransfer.2018.02.013 [3] J. Chen, Z. Ma and Y. Hu, Nonlocal symmetry, Darboux transformation and soliton-cnoidal wave interaction solution for the shallow water wave equation, Journal of Mathematical Analysis and Applications, 2018, 460(2), 987–1003. doi: 10.1016/j.jmaa.2017.12.028 [4] Y. Chen, F. Xu and Y. Hu, Excitation control for three-dimensional Peregrine solution and combined breather of a partially nonlocal variable-coefficient nonlinear Schrödinger equation, Nonlinear Dynamics, 2019, 95, 1957–1964. doi: 10.1007/s11071-018-4670-7 [5] C. Dai, Y. Wang and J. Zhang, Managements of scalar and vector rogue waves in a partially nonlocal nonlinear medium with linear and harmonic potentials, Nonlinear Dynamics, 2020, 102, 379–391. doi: 10.1007/s11071-020-05949-0 [6] C. Ding, Y. Gao, G. Deng and D. Wang, Lax pair, conservation laws, Darboux transformation, breathers and rogue waves for the coupled nonautonomous nonlinear Schrödinger system in an inhomogeneous plasma, Chaos, Solitons & Fractals, 2020, 133, 109580. [7] Y. Ding, M. S. Osman and A. M. Wazwaz, Abundant complex wave solutions for the nonautonomous Fokas-Lenells equation in presence of perturbation terms, Optik, 2019, 181, 503–513. doi: 10.1016/j.ijleo.2018.12.064 [8] Y. Fang, G. Wu, Y. Wang and C. Dai, Data-driven femtosecond optical soliton excitations and parameters discovery of the high-order NLSE using the PINN, Nonlinear Dynamics, 2021, 105, 603–616. doi: 10.1007/s11071-021-06550-9 [9] A. S. Fokas, On a class of physically important integrable equations, Physica D, 1995, 87, 145–150. doi: 10.1016/0167-2789(95)00133-O [10] J. Ha, H. Zhang and Q. Zhao, Exact solurions for a Dirac-type equation with N-fold darboux transformation, Journal of Applied Analysis and Computation, 2019, 9(1), 200–210. doi: 10.11948/2019.200 [11] M. Kaplan, S. San and A. Bekir, On the exact solutions and conservation laws to the Benjamin-Ono equation, Journal of Applied Analysis and Computation, 2018, 8, 1–9. doi: 10.11948/2018.1 [12] J. Lu, X. Hong and Q. Zhao, New exact solutions for coupled SchrödingerBoussinesq equations, Journal of Applied Analysis and Computation, 2021, 11(2), 741–765. doi: 10.11948/20190380 [13] M. Li, H. Fu and C. Wu, General soliton and (semi-)rational solutions to the nonlocal Mel'nikov equation on the periodic background, Studies in Applied Mathematics, 2020, 145(1), 97–136. doi: 10.1111/sapm.12313 [14] X. Liu, Q. Zhou, A. Biswas, A. K. Alzahrani and W. Liu, The similarities and differences of different plane solitons controlled by (3+1)-Dimensional coupled variable coefficient system, Journal of Advanced Research, 2020, 24, 167–173. doi: 10.1016/j.jare.2020.04.003 [15] J. Li and T. Xia, N-soliton solutions for the nonlocal Fokas-Lenells equation via RHP, Applied Mathematics Letters, 2021, 113, 106850. doi: 10.1016/j.aml.2020.106850 [16] B. Li and Y. Ma, Lax pair, Darboux transformation and Nth-order rogue wave solutions for a (2+1)-dimensional Heisenberg ferromagnetic spin chain equation, Computers and Mathematics with Applications, 2019, 77(2), 514–524. doi: 10.1016/j.camwa.2018.09.054 [17] M. S. Osman, Analytical study of rational and double-soliton rational solutions governed by the KdV-Sawada-Kotera-Ramani equation with variable coefficients, Nonlinear Dynamics, 2017, 89, 2283–2289. doi: 10.1007/s11071-017-3586-y [18] M. S. Osman and J. A. T. Machado, New nonautonomous combined multi-wave solutions for (2+1)-dimensional variable coefficients KdV equation, Nonlinear Dynamics, 2018, 93, 733–740. doi: 10.1007/s11071-018-4222-1 [19] M. S. Osman, H. I. Abdel-Gawad and M. A. El Mahdy, Two-layer-atmospheric blocking in a medium with high nonlinearity and lateral dispersion, Results in Physics, 2018, 8, 1054–1060. doi: 10.1016/j.rinp.2018.01.040 [20] M. S. Osman, M. Inc, J. Liu, K. Hosseini and A. Yusuf, Different wave structures and stability analysis for the generalized (2+1)-dimensional CamassaHolm-Kadomtsev-Petviashvili equation, Physica Scripta, 2020, 95, 035229. doi: 10.1088/1402-4896/ab52c1 [21] P. J. Raghuraman, S. Baghya Shree and M. S. Mani Rajan, Soliton control with inhomogeneous dispersion under the influence of tunable external harmonic potential, Waves in Random and Complex Media, 2021, 31(3), 474–485. doi: 10.1080/17455030.2019.1598602 [22] M. Russo, Local and nonlocal solitons in a coupled real system of Landau-Lifshitz equations, Physica D, 2021, 442, 132893. [23] B. Wang, Y. Wang, C. Dai and Y. Chen, Dynamical characteristic of analytical fractional solitons for the space-time fractional Fokas-Lenells equation, Alexandria Engineering Journal, 2020, 59(6), 4699–4707. doi: 10.1016/j.aej.2020.08.027 [24] C. Wang, R. Fan, Z. Zhang and B. Li, Breather positons and rogue waves for the nonlocal Fokas-Lenells equation, Advances in Mathematical Physics, 2021, 9959290. [25] M. Wang and Y. Chen, Dynamic behaviors of mixed localized solutions for the three-component coupled Fokas-Lenells system, Nonlinear Dynamics, 2019, 98, 1781–1794. doi: 10.1007/s11071-019-05285-y [26] X. Xin, Y. Xia, H. Liu and L. Zhang, Darboux transformation of the variable coefficient nonlocal equation, Journal of Mathematical Analysis and Applications, 2020, 490(1), 124227. doi: 10.1016/j.jmaa.2020.124227 [27] X. Xin, L. Zhang, Y. Xia and H. Liu, Nonlocal symmetries and exact solutions of a variable coefficient AKNS system, Journal of Applied Analysis and Computation, 2020, 10(6), 2669–2681. doi: 10.11948/20200022 [28] B. Yang and J. Yang, Transformations between nonlocal and local integrable equations, Studies in applied mathematics, 2018, 140(2), 178–201. doi: 10.1111/sapm.12195 [29] Y. Yang, T. Suzuki and X. Cheng, Darboux transformations and exact solutions for the integrable nonlocal Lakshmanan-Porsezian-Daniel equation, Applied Mathematics Letters, 2020, 99, 105998. doi: 10.1016/j.aml.2019.105998 [30] F. Yu and L. Li, Dynamics of some novel breather solutions and rogue waves for the PT-symmetric nonlocal soliton equations, Nonlinear Dynamics, 2019, 95, 1867–1877. doi: 10.1007/s11071-018-4665-4 [31] H. Zhang, M. Zhang and R. Hu, Darboux transformation and soliton solutions in the parity-time-symmetric nonlocal vector nonlinear Schrödinger equation, Applied Mathematics Letters, 2018, 76, 170–174. doi: 10.1016/j.aml.2017.09.002 [32] Y. Zhang and Y. Liu, Breather and lump solutions for nonlocal DaveyStewartson Ⅱ equation, Nonlinear Dynamics, 2019, 96, 107–113. doi: 10.1007/s11071-019-04777-1 [33] Q. Zhang, Y. Zhang and R. Ye, Exact solutions of nonlocal Fokas-Lenells equation, Applied Mathematics Letters, 2019, 98, 336–343. doi: 10.1016/j.aml.2019.05.015 -
-
Figures(3)
Export File
Citation
Feng Zhang, Yuru Hu, Xiangpeng Xin, Hanze Liu. DARBOUX TRANSFORMATION, EXACT SOLUTIONS OF THE VARIABLE COEFFICIENT NONLOCAL FOKAS-LENELLS EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1544-1557. doi: 10.11948/20210328
Format
Content
DownLoad:
-
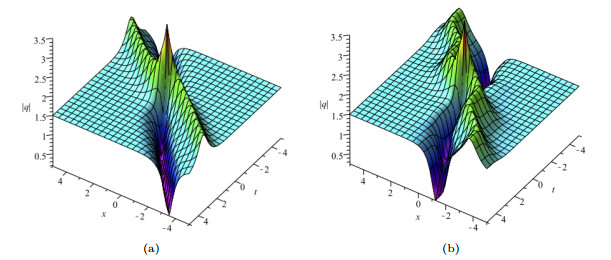
Figure 1. One-soliton solution (4.6) with parameters that are
$ {\lambda _1} = 0.4 + 2i,{\lambda _2} = 0.4 - 2i,{\gamma _1} = {\gamma _2} = 1 $ . (a)$ \delta \left( t \right) = 1 $ . (b)$ \delta \left( t \right) = t^2 $ . -
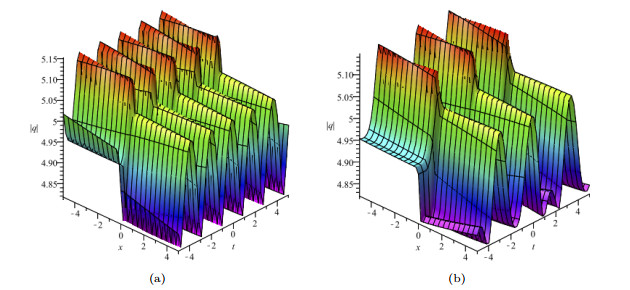
Figure 2. Two-soliton solution with parameters that are
$ {\lambda _1} = i,{\lambda _2} = - 1.0001i,a = - 1.5i,b = 1,{\gamma _1} = - 1,{\gamma _2} = 1 $ . (a)$ \delta \left( t \right) = 1 $ . (b)$ \delta \left( t \right) = {\cos ^2}t $ . -
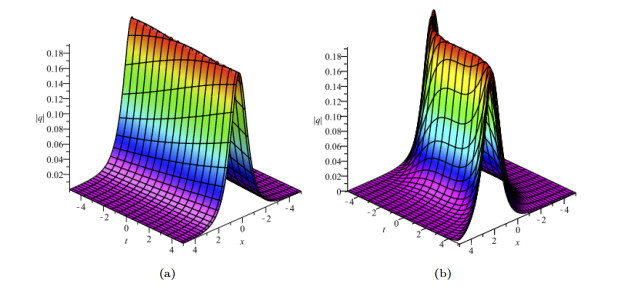
Figure 3. Kink solution with parameters that are
$ {\lambda _1} = 3i,{\lambda _2} = 1 - 3i,a = 5,b = 4,{\gamma _1} = - 1,{\gamma _2} = - 1 $ . (a)$ \delta \left( t \right) = 1 $ . (b)$ \delta \left( t \right) = {\cos}t $ .