| Citation: |
Minghui Jiang, Xue Fang, Junhao Hu. FINITE-TIME STABILITY OF NONAUTONOMOUS AND AUTONOMOUS LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1720-1738. doi: 10.11948/20210397
|
FINITE-TIME STABILITY OF NONAUTONOMOUS AND AUTONOMOUS LINEAR SYSTEMS
-
Abstract
In this research, in view of Lyapunov theory, the finite time stability (FTS) conditions of linear time-delay systems are investigated. Firstly, by using matrix inequality and algebraic inequality methods, the conditions for FTS of nonautonomous and autonomous systems are given respectively. Compared with the existing literature, the judging conditions are easier to verify and have a better conservative type. In addition, by employing the provided FTS theoretical results, several novel criteria for ensuring the stabilization of autonomous delay systems and the stability of impulsive switched nonautonomous time-varying systems are obtained. Eventually, several concrete examples are put forward to validate the theoretical findings.
-
Keywords:
- Finite time stability /
- time delay /
- Lyapunov functional /
- impulsive switching
-
-
References
[1] F. Amato, M. Ariola and P. Dorato, Finite time control of linear systems subject to parametric uncertainties and disturbances, Automatica, 2001, 37(9), 1459–1463. doi: 10.1016/S0005-1098(01)00087-5 [2] F. Amato, M. Ariola and C. Cosentino, Finite-time stabilization via dynamic output feedback, Automatica, 2006, 42(2), 337–342. doi: 10.1016/j.automatica.2005.09.007 [3] F. Amato, M. Ariola and C. Cosentino, Finite-time stability of linear time-varying systems: analysis and controller design, IEEE Transactions on Automatic Control, 2010, 55(4), 1003–1008. doi: 10.1109/TAC.2010.2041680 [4] F. Amato, M. Ariola and C. Cosentino, Finite-time control of discrete-time linear systems: analysis and design, Automatica, 2010, 46(5), 919–924. doi: 10.1016/j.automatica.2010.02.008 [5] F. Amato, C. Cosentino and A. Merola, Sufficient conditions for finite-time stability and stabilization of nonlinear quadratic systems, IEEE Transactions on Automatic Control, 2010, 55(2), 430–434. doi: 10.1109/TAC.2009.2036312 [6] R. Ambrosino, C. Cosentino, F. Arnato and M. Ariola, Finite-time stability of linear time-varying systems with jumps, Automatica, 2009, 45(5), 1354–1358. doi: 10.1016/j.automatica.2008.12.016 [7] R. Ambrosino, F. Calabrese, C. Cosentino and G. D. Tommasi, Sufficient conditions for finite-time stability of impulsive dynamical systems, IEEE Transactions on Automatic Control, 2009, 54(4), 861–865. doi: 10.1109/TAC.2008.2010965 [8] F. Amato, R. Ambrosino, C. Cosentino and G. D. Tommasi, Finite-time stabilization of impulsive dynamical linear systems, Nonlinear Analysis, 2011, 5(1), 89–101. [9] F. Amato, R. Ambrosino, M. Ariola and G. D. Tommasi, Robust finite-time stability of impulsive dynamical linear systems subject to norm-bounded uncertainties, International Journal of Robust and Nonlinear Control, 2011, 21, 1080–1082. doi: 10.1002/rnc.1620 [10] G. Arthi, N. Brindha and Y. Ma, Finite-time stability of multiterm fractional nonlinear systems with multistate time delay, Advances in Difference Equations, 2021, 2021, 1–15. doi: 10.1186/s13662-020-03162-2 [11] G. Chen and Y. Yang, New sufficient conditions for finite time stability of nonlinear time delay systems, Asian Journal of Control, 2019, 21, 2321–2329. doi: 10.1002/asjc.1883 [12] M. Chen and J. Sun, Delay-dependent conditions for finite time stability of linear time-varying systems with delay, Asian Journal of Control, 2020, 22(2), 924–933. doi: 10.1002/asjc.2059 [13] Z. Cai, L. Huang and Z. Wang, Finite-fixed-time stability of nonautonomous functional differential inclusion: Lyapunov approach involving indefinite derivative, IEEE transactions on neural networks and learning systems, 2021, 1–12. [14] G. Chen and Y. Yang, New necessary and sufficient conditions for finite-time stability of impulsive switched linear time-varying systems, IET Control Theory and Applications, 2018, 12, 140–148. doi: 10.1049/iet-cta.2017.0252 [15] H. Du, X. Lin and S. Li, Finite-time boundedness and stabilization of switched linear systems, Kybernetika, 2010, 46(5), 870–889. [16] G. Garcia, S. Tarbouriech and J. Bernussou, Finite-time stabilization of linear time-varying continuous systems, IEEE Transactions on Automatic Control, 2009, 54(2), 364–369. doi: 10.1109/TAC.2008.2008325 [17] Y. Hong, J. Huang and Y. Xu, On an output feedback finite time stabilization problem, IEEE Transactions on Automatic Control, 2001, 46(2), 305–309. doi: 10.1109/9.905699 [18] W. Haddad and J. Lee, Finite-time stability of discrete autonomous systems, Automatica, 2020, 122, 109282. doi: 10.1016/j.automatica.2020.109282 [19] I. Hien, An explicit criterion for finite-time stability of linear nonautonomous systems with delays, Applied Mathematics Letters, 2014, 30, 12–18. doi: 10.1016/j.aml.2013.12.005 [20] I. Hien and D. Son, Finite-time stability of a class of non-autonomous neural networks with heterogeneous proportional delays, Applied Mathematics and Computation, 2015, 251, 14–23. doi: 10.1016/j.amc.2014.11.044 [21] X. He, X. Li and J. Juan, Finite-time stability and stabilization for time-varying systems, Chaos, Solitons and Fractals, 2021, 111076. [22] G. V. Kamenkov, On stability of motion over a finite interval of time, Journal of Applied Mathematics and Mechanics, 1953, 17, 529–540. [23] V. Kumar, M. Djemašª, M. Defoort and M. Malik, Finite-time stability and stabilization results for switched impulsive dynamical systems on time scales, Journal of the Franklin Institute, 2020, 358, 674–698. [24] X. Lin, K. Liang and H. Li, Finite-time stability and stabilization for continuous systems with additive time-varying delays, Circuits, Systems, and Signal Processing, 2017, 36, 2971–2990. doi: 10.1007/s00034-016-0443-z [25] X. Luan, F. Liu and P. Shi, Finite-time filtering for non-linear stochastic systems with partially known transition jump rates, IET Control Theory and Applications, 2010, 4(5), 735–745. doi: 10.1049/iet-cta.2009.0014 [26] X. Li, X. Yang and S. Song, Lyapunov conditions for finite-time stability of time-varying time-delay systems, Automatica, 2019, 103, 135–140. doi: 10.1016/j.automatica.2019.01.031 [27] J. Puangmalai, J. Tongkum and T. Rojsiraphisal, Finite-time stability criteria of linear system with non-differentiable time-varying delay via new integral inequality, Mathematica and Computers in Simulation, 2020, 171, 170–186. doi: 10.1016/j.matcom.2019.06.013 [28] Y. Shen, Finite-time control of linear parameter-varying systems with normbounded exogenous disturbance, Journal of Control Theory and Applications, 2008, 6(2), 184–188. doi: 10.1007/s11768-008-6176-1 [29] Y. Tian, Y. Cai, Y. Sun and H. Gao, Finite-time stability for impulsive switched delay systems with nonlinear disturbances, Journal of the Franklin Institute, 2016, 353, 3578–3594. doi: 10.1016/j.jfranklin.2016.06.021 [30] X. Wang, S. Huang, W. Zou and Z. Xiang, Finite-time stabilization for a class of nonlinear systems with time-varying delay, International Journal of Robust and Nonlinear Control, 2020, 30, 3164–3178. doi: 10.1002/rnc.4925 [31] Y. Wang, X. Shi, Z. Zuo, M. Chen and Y. Shao, On finite-time stability for nonlinear impulsive switched systems, Nonlinear Analysis: Real World Applications, 2013, 14(1), 807–814. doi: 10.1016/j.nonrwa.2012.08.003 [32] J. Xu and J. Sun, Finite-time stability of linear time-varying singular impulsive systems, IET Control Theory and Applications, 2010, 4(10), 2239–2244. doi: 10.1049/iet-cta.2010.0242 [33] W. Xiang and J. Xiao, $H_\infty$ finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance, Journal of the Franklin Institute, 2011, 348(2), 331–352. doi: 10.1016/j.jfranklin.2010.12.001 CrossRef $H_\infty$ finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance" target="_blank">Google Scholar
[34] Y. Yang, J. Li and G. Chen, Finite-time stability and stabilization of nonlinear stochastic hybrid systems, Journal of Mathematical Analysis and Applications, 2009, 356, 338–345. doi: 10.1016/j.jmaa.2009.02.046 [35] X. Yang and X. Li, Finite-time stability of linear non-autonomous systems with time-varying delays, Advances in Difference Equations, 2018, 2018, 101–110. doi: 10.1186/s13662-018-1557-3 [36] S. Zhao, J. Sun and L. Liu, Finite-time stability of linear time-varying singular systems with impulsive effects, International Journal of Control, 2008, 81(11), 1824–1829. doi: 10.1080/00207170801898893 [37] B. Zhou, Finite-time stability analysis and stabilization by bounded linear time-varying feedback, Automatica, 2020, 121, 109191. doi: 10.1016/j.automatica.2020.109191 [38] K. Zimenko, D. Efimov, A. Polyakov and A. Kremlev, On necessary and sufficient conditions for output finite-time stability, Automatica, 2021, 125, 109427. doi: 10.1016/j.automatica.2020.109427 [39] B. Zhou, Finite-time stabilization of linear systems by bounded linear time-varying feedback, Automatica, 2020, 108760. [40] G. Zong, X. Wang and H. Zhao, Robust finite-time guaranteed cost control for impulsive switched systems with time-varying delay, International Journal of Control, Automation, and Systems, 2017, 15, 113–121. doi: 10.1007/s12555-015-0314-6 -
-
Figures(10)
Export File
Citation
Minghui Jiang, Xue Fang, Junhao Hu. FINITE-TIME STABILITY OF NONAUTONOMOUS AND AUTONOMOUS LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1720-1738. doi: 10.11948/20210397
Format
Content
DownLoad:
-
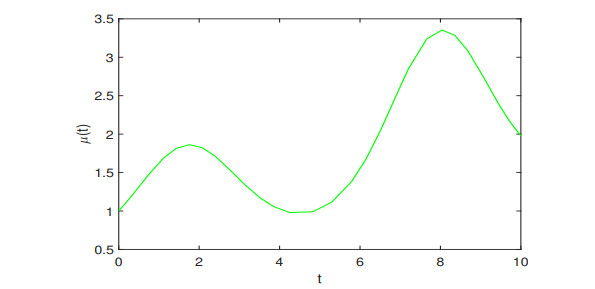
Figure 1.
The dynamical behaviors of
$ \mu(t) $ -
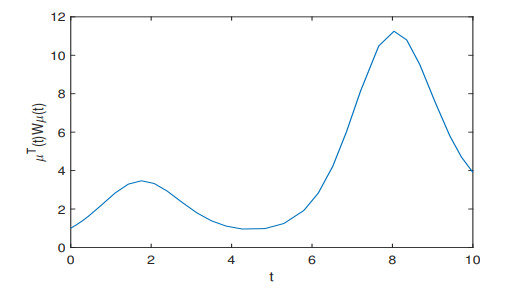
Figure 2.
The dynamical behaviors of
$ \mu^T(t)W\mu(t) $ $ \beta_1=1, \beta_2=44.7230, W=I, \mathcal{T}=6.3 $ -
Figure 3.
The trajectories of
$ \mu_{1}(t), \mu_{2}(t) $ $ \mu_1(0)=0.7070, \mu_2(0)=-0.707. $ -
Figure 4.
The trajectories of
$ \mu^T(t)W\mu(t) $ $ t. $ -
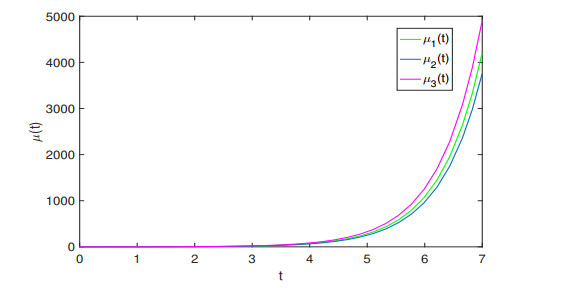
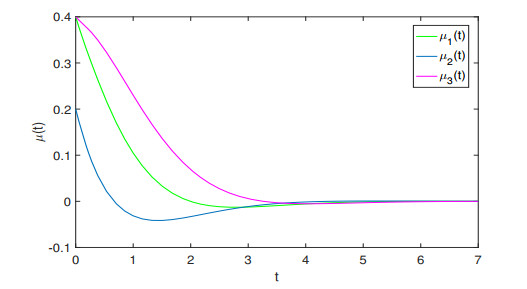
Figure 5.
The dynamical behaviors of
$ \mu(t) $ $ \mu_1(0)=0.4, \mu_2(0)=0.2, \mu_3(0)=0.4 $ -
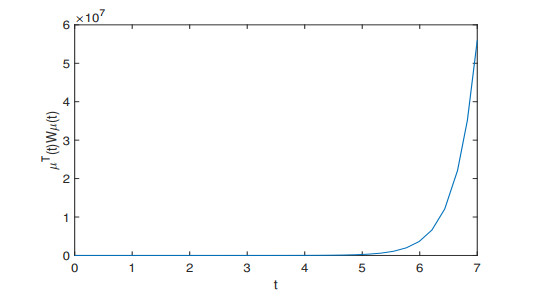
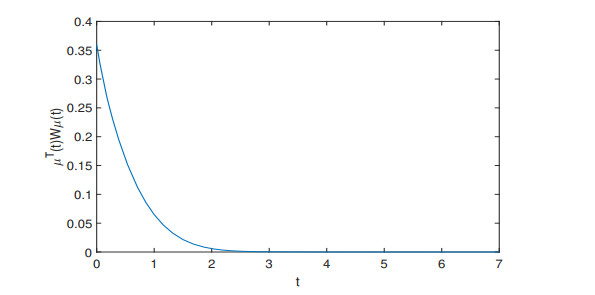
Figure 6.
The dynamical behaviors of
$ \mu^T(t)W\mu(t) $ $ \beta_1=0.36, \beta_2= 3, W=I, \mathcal{T}=7 $ -
Figure 7.
The dynamical behaviors of
$ \mu(t) $ -
Figure 8.
The dynamical behaviors of
$ \mu^T(t)W\mu(t) $ $ \beta_1=0.36, \beta_2= 3, W=I, \mathcal{T}=7 $ -
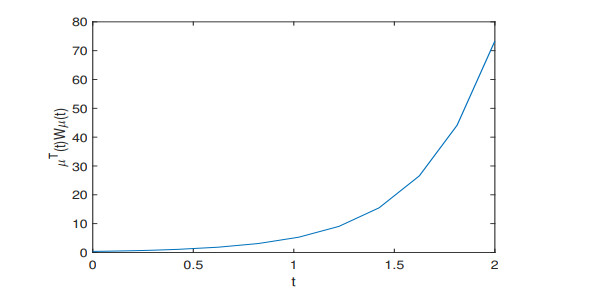
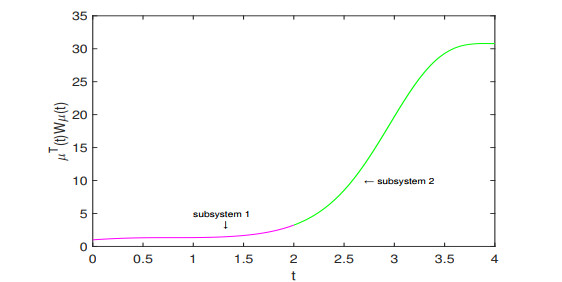
Figure 9.
The dynamical behaviors of
$ \mu^T(t)W\mu(t) $ -
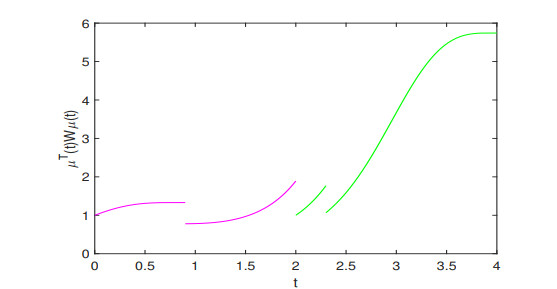
Figure 10.
The dynamical behaviors of
$ \mu^T(t)W\mu(t) $