| Citation: |
Shuangshuang Xia, Zenggui Wang. LIE SYMMETRIES, GROUP INVARIANT SOLUTIONS AND CONSERVATION LAWS OF IDEAL MHD EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1959-1986. doi: 10.11948/20210410
|
LIE SYMMETRIES, GROUP INVARIANT SOLUTIONS AND CONSERVATION LAWS OF IDEAL MHD EQUATIONS
-
Abstract
In this paper, the method of Lie symmetry is used to study the incompressible ideal MHD equations. We derive the infinitesimal generators of MHD by using Lie symmetry method. Then, we get the group invariant solutions to MHD based on the group transformation and known solutions. An one-dimensional optimal system which only depends on the commutator of Lie algebras is constructed. Through the similarity transformation of the optimal system, we obtain the 1 + 1-dimensional reduced partial differential equations, and further obtain the exact solutions of these equations, such as Bell soliton solution, junction soliton solution and seed solution. In addition, we prove the nonlinear self-adjoint and conservation laws of the MHD equations using the Ibragimov method. Finally, the classical symmetry and solutions to incompressible ideal MHD equations with initial conditions left invariant are discussed.
-
-
References
[1] A. H. Abdel-Kader, M. S. Abdel-Latif and H. M. Nour, Some new exact solutions of the modified kdv equation using Lie point symmetry method, Int. J. Appl. Comput. Math., 2017, 3(1), 1163-1171. [2] M. S. Abdel-Latif, A. H. Abdel-Kader and H. M. Nour, Exact implicit solution of nonlinear heat transfer in rectangular straight fin using symmetry reduction methods, Appl. Math., 2015, 10(2), 864-877. [3] S. K. Al-Nassar and J. Goard, Symmetries for initial value problems, Applied Mathematics Letters, 2014, 28, 56-59. doi: 10.1016/j.aml.2013.09.012 [4] S. K. Al-Nassar, Nonclassical symmetry analysis of second order parabolic partial differential equations, University of Wollongong, 2012. [5] H. Baran, I. S. Krasil'shchik, O. I. Morozov and P. Voják, Symmetry reductions and exact solutions of Lax integrable 3-dimensional systems, Journal of Mathematical Physics, 2015, 21, 643-671. [6] Y. Bai and D. Su, One-Dimensional Optimal System and Invariant Solution of Poisson Equation, Journal of Mathematics, 2018, 38(4), 706-712. [7] Q. Chen, C. Miao and Z. Zhang, On the well-posedness of the ideal MHD equations in the Triebel-lizorkin spaces, Arch. Rational Mech. Anal., 2010, 195, 561-578. doi: 10.1007/s00205-008-0213-6 [8] Y. Chan, Z. Han and L. Zhang, A direct algorithm maple package of One-dimensional optimal system for group invariant solutions, Communications in Theoretical Physics, 2018, 69(1), 14-22. doi: 10.1088/0253-6102/69/1/14 [9] F. Demontis, B. Prinari, B. C. Mee, et al., The inverse scattering transform for the focusing nonlinear Schrödinger equation with asymmetric boundary conditions, J. Math. Phys., 2014, 55(10), 101505. doi: 10.1063/1.4898768 [10] G. Duvaut and J. L. Lions, Inéquations en thermoélasticité et magnétohydrodynamique, Archive for Rational Mechanics and Analysis, 1972, 46, 241-279. doi: 10.1007/BF00250512 [11] M. Dong, S. Tian, X. Yan, et al., Bäcklund transformation, rogue wave solutions and interaction phenomena for a (3+1)-dimensional B-type Kadomtsev-Petviashvili-Boussinesq equation, Nonlinear Dyn., 2018, 92(2), 709-720. doi: 10.1007/s11071-018-4085-5 [12] B. Gao and S. Zhang, Invariant solutions of the normal hyperbolic mean curvature flow with dissipation, Arch. Math., 2020, 114, 227-239. doi: 10.1007/s00013-019-01397-4 [13] F. Gao and Z. Wang, Nonlinear self-adjointness and conservation laws for the modified dissipative hyperbolic geometric flow equation, Journal of Geometry and Physics, 2021, 167, 104304. doi: 10.1016/j.geomphys.2021.104304 [14] N. H. Ibragimov, A new conservation theorem, Journal of Mathematical Physics, 2007, 333, 311-328. [15] N. H. Ibragimov and E. D. Avdonina, Nonlinear self-adjointness, conservation laws and the construction of solutions of partial differential equations using conservation laws, Russ. Math. Surv., 2013, 68(5), 889-921. doi: 10.1070/RM2013v068n05ABEH004860 [16] L. Li, C. Duan and F. Yu, An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (MKdV), Physics Letters A, 2019, 383, 1578-1582. doi: 10.1016/j.physleta.2019.02.031 [17] B. Liu and T. Ren, Global well-posedness to the cauchy problem of 3D incompressible Two-fluid MHD model with small initial data, Journal of lishui university, 2016, 38(2). [18] M. Liu and H. Dong, On the existence of solution, Lie symmetry analysis and conservation law of magnetohydrodynamic equations, Commun. Nonlinear Sci. Numer. Simulat., 2020, 87, 105277. doi: 10.1016/j.cnsns.2020.105277 [19] M. Liu and R. Yuan, On the well-posedness of strong solution to ideal magnetohydrodynamic equations, Int. J. comput. Math., 2017, 94, 2458-2465. doi: 10.1080/00207160.2017.1283413 [20] E. Noether, Invariante variations probleme, Mathematisch-Physikalische Klasse, 1918, 2, 235-257. [21] A. P. Oskolkov, The uniqueness and global solvability of boundary-value problems for the equations of motion for aqueous solutions of polymers, Journal of Soviet Mathematics, 1977, 427-455. [22] A. P. Oskolkov, On a quasilinear parabolic system with a small parameter, approximating the Navier-Stokes system of equations, Zap. Nauchn. Sem. LOMI, 1971, 21, 79-103. [23] M. Osman, et al., Double-wave solutions and Lie symmetry analysis to the (2+1)-dimensional coupled Burgers equations, Chinese J. Phy., 2020, 63, 122-129. [24] M. Osman, et al., Double-wave solutions and Lie symmetry analysis to the (2+ 1)-dimensional coupled Burgers equations, Chinese J. Phy., 2020, 63, 122-129. [25] Y. Ohta and J. Yang, General rogue waves in the focusing and defocusing AblowitzšCLadik equations, J. Phys. A: Math. Theor., 2014, 47, 255201. doi: 10.1088/1751-8113/47/25/255201 [26] B. Prinari and F. Vitale, Inverse scattering transform for the focusing Ablowitz-Ladik system with nonzero boundary conditions, Stud. Appl. Math., 2016, 137, 28-52. doi: 10.1111/sapm.12103 [27] H. O. Roshid and W. Ma, Dynamics of mixed lump-solitary waves of an extended (2+1)-dimensional shallow water wave model, Phys. Lett. A, 2018, 382, 3262-3268. doi: 10.1016/j.physleta.2018.09.019 [28] G. Wang, Symmetry analysis and rogue wave solutions for the (2+1)-dimensional nonlinear Schrödinger equation with variable coefficients, Appl. Math. Lett., 2016, 56, 56-64. doi: 10.1016/j.aml.2015.12.011 [29] J. Wu, Viscous and inviscid magnetohydrodynamic equations, Journal of Mathematique, 1997, 73, 250-265. [30] J. Wu, Generlized MHD equations, Journal of Differential equations, 2003, 195, 284-312. doi: 10.1016/j.jde.2003.07.007 [31] X. Wen and Z. Yan, Modulational instability and dynamics of multi-rogue wave solutions for the discrete Ablowitz-Ladik equation, J. Math. Phys., 2018, 59, 73511. doi: 10.1063/1.5048512 [32] X. Wen and D. Wang, Modulational instability and higher order rogue wave solutions for the generalized discrete Hirota equation, An International Journal Reporting Research on Wave Phenomena, 2018, 79, 84-97. [33] S. Xia and Z. Wang, Group invariant solutions and conservation laws of (2+1)-dimensional AKNS equation, Journal of Geometry and Physics, 2022, 175, 104486. [34] Y. Yang and Y. Zhu, Darboux-Bäcklund transformation, breather and rogue wave solutions for Ablowitz-Ladik equation, Optik, 2020, 217, 164920. doi: 10.1016/j.ijleo.2020.164920 [35] Z. Zhao, Bäcklund transformations, rational solutions and soliton-cnoidal wave solutions of the modified Kadomtsev-Petviashvili equation, Applied Mathematics Letters, 2019, 89, 103-110. doi: 10.1016/j.aml.2018.09.016 [36] Z. Zhang and Y. Chen, Classical and nonclassical symmetries analysis for initial value problems, Physics Letters A, 2010, 374(9), 1117-1120. doi: 10.1016/j.physleta.2009.12.052 -
-
Figures(9) / Tables(3)
Export File
Citation
Shuangshuang Xia, Zenggui Wang. LIE SYMMETRIES, GROUP INVARIANT SOLUTIONS AND CONSERVATION LAWS OF IDEAL MHD EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1959-1986. doi: 10.11948/20210410
Format
Content
DownLoad:
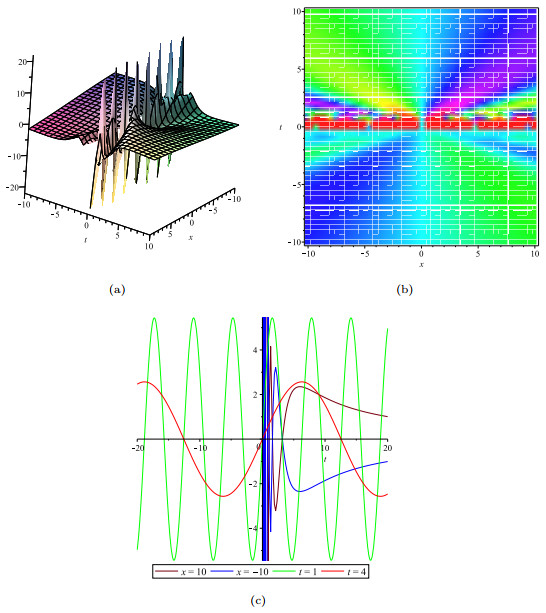
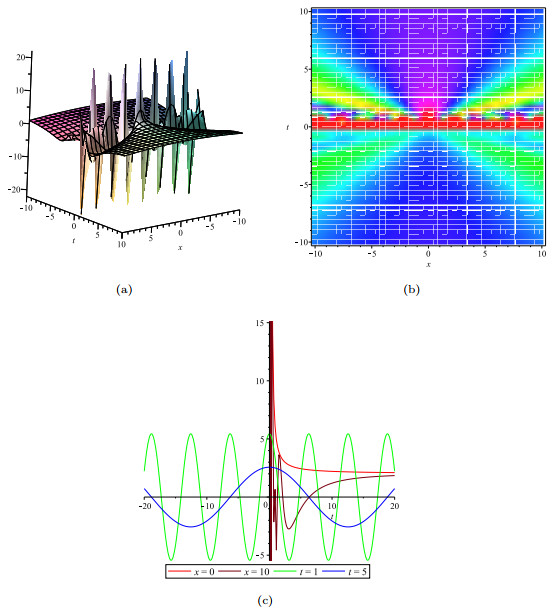
- Figure 1. The solution u with y=1: (a). indicates the solitons solution; (b).indicates the density plot of u; (c). indicates the wave track along the t-axis at t=1, t=5 and along the x-axis at x=0, x=10.
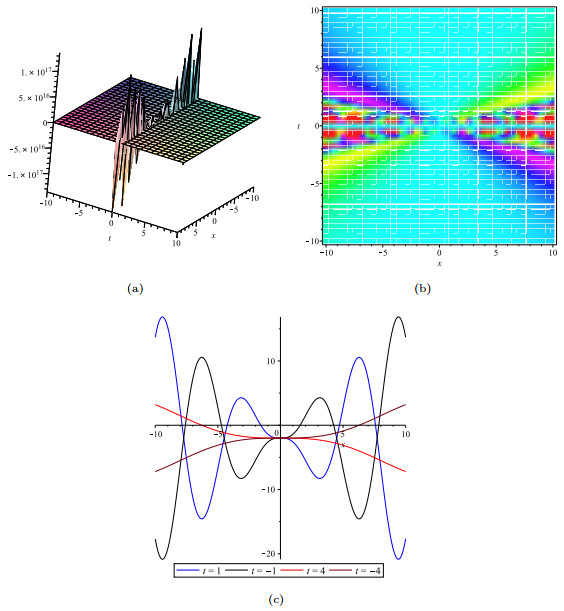
- Figure 2. The solution v with y=1 : (a). indicates the solitons solution; (b).indicates the density plot of v; (c). indicates the wave track along the t-axis at t=1, t=4 and along the x-axis at x=-10, x=10.
- Figure 3. The solution p with y=0: (a). indicates the solitons solution; (b).indicates the density plot of p; (c). indicates the wave track along the t-axis at t=±1, t=±4.
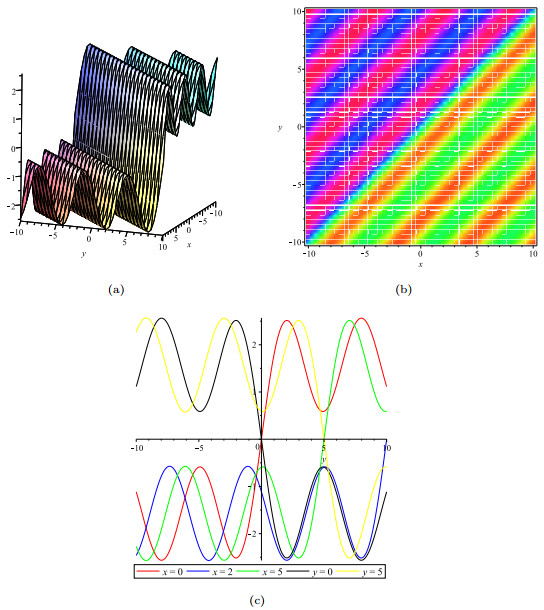
- Figure 4. The solution u: (a). indicates the multiple soliton solution; (b).indicates the density plot of u; (c). indicates the wave track along the x-axis at x=0, x=2, x=5 and along the y-axis at x=0, y=5.
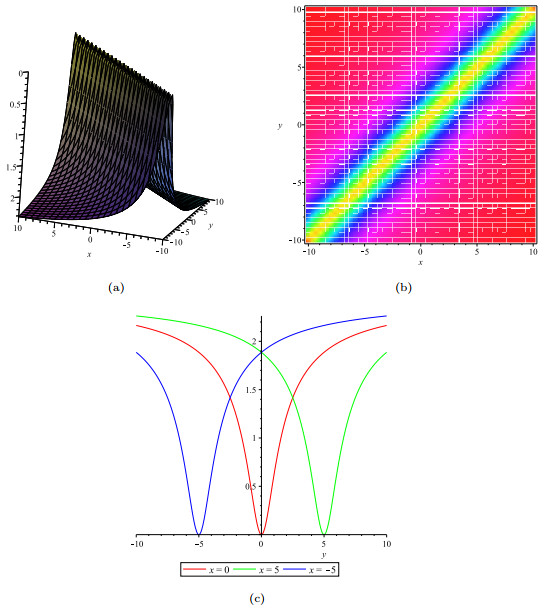
- Figure 5. The solution b: (a). indicates the bright soliton solution; (b).indicates the density plot of u; (c). indicates the wave track along the x-axis at x=0, x=±5.
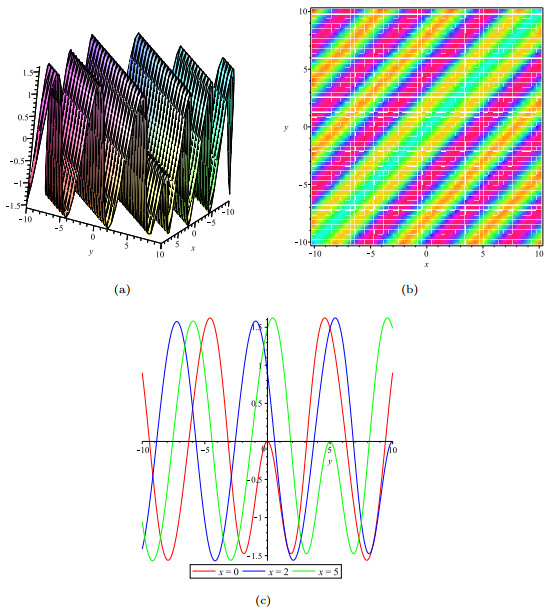
- Figure 6. The solution u: (a). indicates the multiple soliton solution; (b).indicates the density plot of u; (c). indicates the wave track along the x-axis at x=0, x=2, x=5.
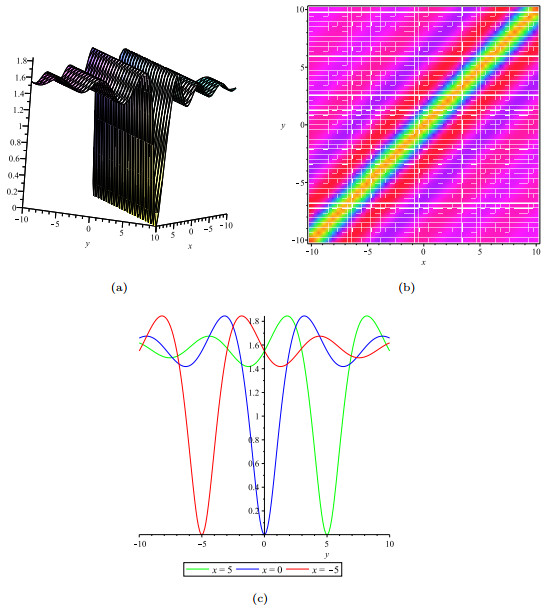
- Figure 7. The solution b: (a). indicates the break multiple soliton solution; (b).indicates the density plot of u; (c). indicates the wave track along the x-axis at x=0, x=±5.
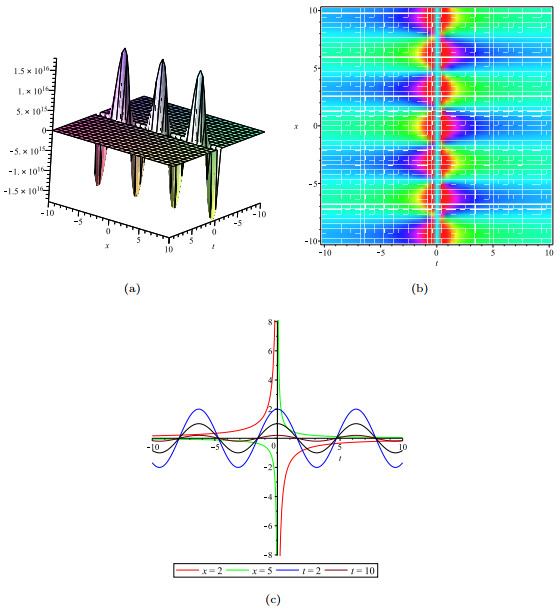
- Figure 8. The solution u: (a). indicates the periodic soliton solution; (b).indicates the density plot of u; (c). indicates the wave track along the x-axis at x=2, x=5 and along the t-axis at t=2, t=10.
-
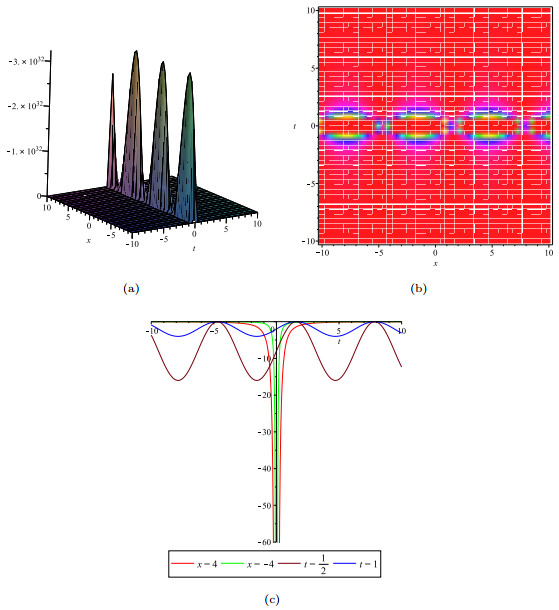
Figure 9. The solution v: (a). indicates the bell soliton solution; (b).indicates the density plot of v; (c). indicates the wave track along the x-axis at x=±4 and along the t-axis at
$ t=\frac{1}{2} $ , t=1.