| Citation: |
Jinsen Zhuang, Yan Zhou. BIFURCATIONS OF SOLITARY WAVES, PERIODIC PEAKONS AND COMPACTONS OF A COUPLED NONLINEAR WAVE EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1997-2013. doi: 10.11948/20210424
|
BIFURCATIONS OF SOLITARY WAVES, PERIODIC PEAKONS AND COMPACTONS OF A COUPLED NONLINEAR WAVE EQUATION
-
Abstract
For a coupled nonlinear wave equation system, its travelling wave system just is a singular traveling wave system of the first class depending on nine parameters. By using the bifurcation theory and method of dynamical systems and the theory of singular traveling wave systems, in this paper, we show that there exist parameter groups such that this singular system has kink and anti-kink wave solutions, periodic solutions, periodic peakons and compactons as well as different solitary wave solutions.
-
-
References
[1] A. Biswas, M. Ekici, A. Sonmezoglu and R. T. Alqahtani, Optical soliton perturbation with full nonlinearity for Fokas–Lenells equation, Optik, 2018, 165, 29-34, doi: 10.1016/j.ijleo.2018.03.094 [2] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971. [3] J. Chehab and D. Dutykh, On time relaxed schemes and formulations for dispersive wave equations, AIMS Math., 2019, 4, 254-278. doi: 10.3934/math.2019.2.254 [4] C. Gu, On the Backlund transformations for the generalized hierarchies of compound MKdV-SG equations, Lett. Math. Phys., 1986, 12, 31-41. doi: 10.1007/BF00400301 [5] C. Guha-Roy, Solitary wave solutions of a system of coupled nonlinear equation, J. Math. Phys., 1987, 28, 2087. doi: 10.1063/1.527419 [6] C. Guha-Roy, Exact solutions to a coupled nonlinear equation, Inter, J. Theor. Phys., 1988, 27, 447. doi: 10.1007/BF00669393 [7] X. Hu and Z. Zhu, A Backlund transformation and nonlinear superposition formula for the Belov-Chaltikian lattice, J. Phys. A, 1998, 31, 4755-4761. doi: 10.1088/0305-4470/31/20/012 [8] R. Hirota, X. Hu and X. Tang, A vector potential KdV equation and vector Ito equation: soliton solutions, bilinear Backlund transformations and Lax pairs, J. Math. Anal. Appl., 2003, 288, 326-348. doi: 10.1016/j.jmaa.2003.08.046 [9] W. Li and X. Geng, Darboux transformation of a differential-difference equation and its explicit solutions, Chinese Phys. Lett., 2006, 23, 1361-1364. doi: 10.1088/0256-307X/23/6/002 [10] S. Lou and J. Lu, Special solutions from the variable separation approach: the Davey-Stewartson equation, J. Phys. A, 1996, 29, 4209-4215. doi: 10.1088/0305-4470/29/14/038 [11] Z. Liu and T. Qian, Peakons of the Camassa-Holm equation, Appl. Math. Model., 2002, 26, 473-480. doi: 10.1016/S0307-904X(01)00086-5 [12] D. Lu and G. Yang, Compacton solutions and peakon solutions for a coupled nonlinear wave equation, Inter. J. Nonlinear Science, 2007, 4, 31-36. [13] X. Liu and C. He, New exact solitary wave solutions of a coupled nonlinear wave equation, Abstr. Appl. Anal., 2013, 1-7. [14] J. Li and G. Chen, Bifurcations of travelling wave solutions for four classes of nonlinear wave equations, Int. J. Bifurcation and Chaos, 2005, 15, 3973-3998. doi: 10.1142/S0218127405014416 [15] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifurcation and Chaos, 2007, 17, 4049-4065. doi: 10.1142/S0218127407019858 [16] J. Li, Y. Zhang and X. Zhao, On a class of singular nonlinear traveling wave equations (Ⅱ): an example of GCKdV equations, Int. J. Bifurcation and Chaos, 2009, 19, 1955-2007. [17] J. Li, W. Zhou and G. Chen, Understanding peakons, periodic peakons and compactons via a shallow water wave equation, Int. J. Bifurcation and Chaos, 2016, 26(12), 1650207. doi: 10.1142/S0218127416502072 [18] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [19] W. Ma, Complexiton solutions of the Korteweg-de Vries equation with selfconsistent sources, Chaos Soliton Fract., 2005, 26, 1453-1458. doi: 10.1016/j.chaos.2005.03.030 [20] Y. Shang, Explicit and exact solutions for a coupled nonlinear wave equation, J. Ningxia University (Natural Science Edition), 2000, 21, 290-294. [21] X. Xu and J. Zhang, New exact and explicit solitary wave solutions to a class of coupled nonlinear equation, Commun. Nonlinear Sci., 1998, 3, 189-193. doi: 10.1016/S1007-5704(98)90015-6 -
-
Figures(11)
Export File
Citation
Jinsen Zhuang, Yan Zhou. BIFURCATIONS OF SOLITARY WAVES, PERIODIC PEAKONS AND COMPACTONS OF A COUPLED NONLINEAR WAVE EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1997-2013. doi: 10.11948/20210424
Format
Content
DownLoad:
-
Figure 1. The phase portrait of system (1.8) for
$ g\epsilon>0 , c\gamma>0 $ . -
Figure 2. The phase portrait of system (1.8) for
$ g\epsilon>0 , c\gamma<0 $ . -
Figure 3. The phase portrait of system (1.8) for
$ g\epsilon<0, c\gamma>0 $ . -
Figure 4. The phase portrait of system (1.8) for
$ g\epsilon<0, c\gamma<0 $ . -
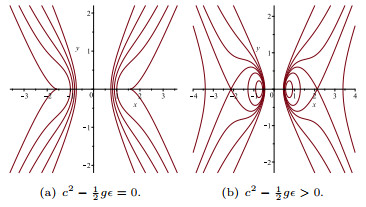
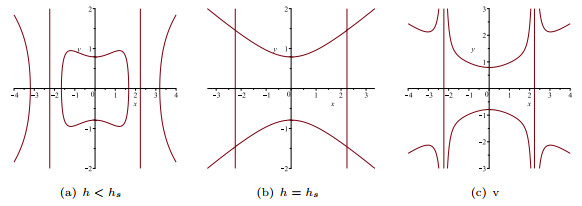
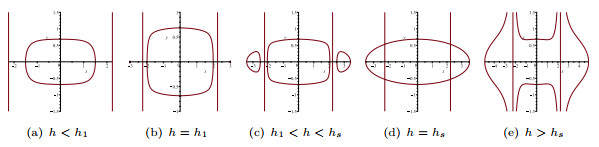
Figure 5. The changes of the level curves for
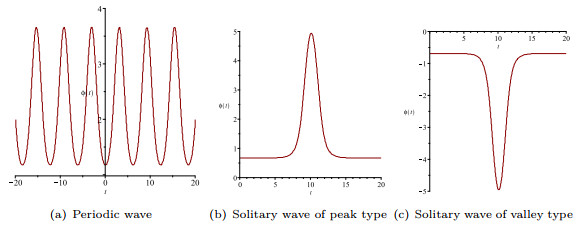
$ g\epsilon>0 $ ,$ c\gamma>0 , c^2-\frac12g\epsilon>0 $ . - Figure 6. The periodic wave and solitary wave of system (1.8).
-
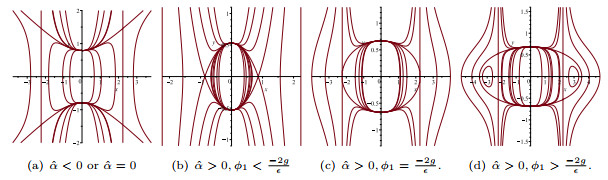
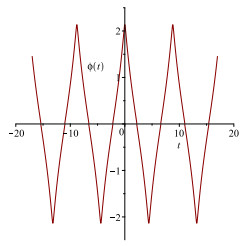
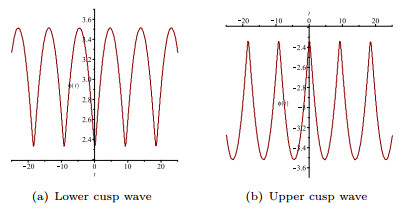
Figure 7. The changes of the level curves defined by (1.9) for
$ g\epsilon<0 $ ,$ c\gamma>0, \hat{\alpha}<0 $ . - Figure 8. The periodic peakon or sawtooth cusp wave of system (1.8).
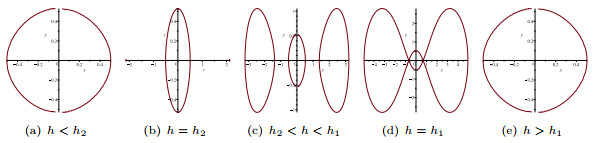
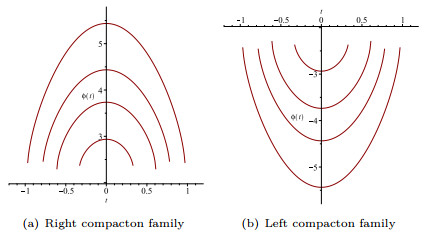
- Figure 9. The compacton solution families of system (1.8).
-
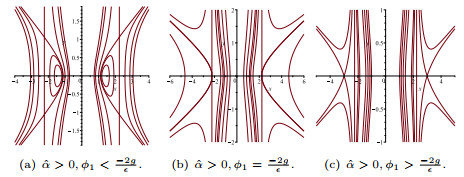
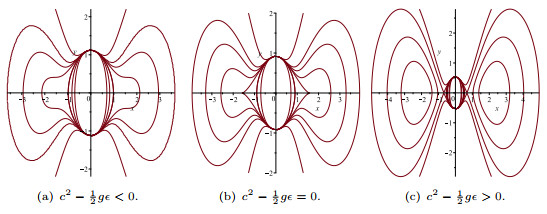
Figure 10. The changes of the level curves for
$ g\epsilon<0 $ ,$ c\gamma>0 $ ,$ \hat{\alpha}>0, \phi_1>\frac{-2g}{\epsilon} $ . - Figure 11. The periodic peakons of system (1.8).