| Citation: | Yu Yang, Jueyu Wang, Shengliang Zhang, Tonghua Zhang. DYNAMICAL ANALYSIS OF A FRACTIONAL ORDER HCV INFECTION MODEL WITH ACUTE AND CHRONIC AND GENERAL INCIDENCE RATE[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2283-2298. doi: 10.11948/20210430 |
DYNAMICAL ANALYSIS OF A FRACTIONAL ORDER HCV INFECTION MODEL WITH ACUTE AND CHRONIC AND GENERAL INCIDENCE RATE
-
Abstract
This paper is concerned with a fractional order HCV infection model with acute and chronic and general incidence rate. We first give the positivity and boundedness of the solution for this model. Then, we establish the dynamical behavior of this model in terms of $ \mathcal{R}_{0}^{\alpha} $. Numerical simulations are given to verify the obtained theoretical results.
-
Keywords:
- Fractional order /
- HCV infection model /
- global stability /
- Lyapunov function
-

-
References
[1] T. A. R. Aggarwal and Y. A. Raj, A fractional order HIV-TB co-infection model in the presence of exogenous reinfection and recurrent TB, Nonlinear Dyn., 2021, 104, 4701-4725. doi: 10.1007/s11071-021-06518-9 [2] E. Ahmed, A. M. A. El-Sayed and H. A. A. El-Saka, On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems, Phys. Lett. A, 2006, 358, 1-4. doi: 10.1016/j.physleta.2006.04.087 [3] L. Cai and X. Li, A note on global stability of an SEI epidemic model with acute and chronic stages, Appl. Math. Comput., 2008, 196, 23-930. [4] Y. Chen, F. Liu, Q. Yu and T. Li, Review of fractional epidemic models, Appl. Math. Model., 2021, 97, 281-307. doi: 10.1016/j.apm.2021.03.044 [5] N. D. Cong, T. S. Doan, S. Siegmund and H. T. Tuan, Linearized asymptotic stability for fractional differential equations, Electron. J. Qual. Theo. Diff. Equ., 2016, 39, 1-13. [6] N. D. Cong, T. S. Doan, S. Siegmund and H. T. Tuan, An instability theorem for nonlinear fractional differential systems, Discrete Contin. Dyn. Syst. Ser. B, 2017, 22, 3079-3090. [7] J. Cui, S. Zhao, S. Guo, Y. Bai, X. Wang and T. Chen, Global dynamics of an epidemiological model with acute and chronic HCV infections, Appl. Math. Lett., 2020, 103, 106203. doi: 10.1016/j.aml.2019.106203 [8] K. Diethelm, The Analysis of Fractional Differential Equations, Springer, Berlin, 2010. [9] K. Diethelm, A fractional calculus based model for the simulation of an outbreak of dengue fever, Nonlinear Dyn., 2013, 71, 613-619. doi: 10.1007/s11071-012-0475-2 [10] K. M. Furati, I. O. Sarumi and A. Q. M. Khaliq, Fractional model for the spread of COVID-19 subject to government intervention and public perception, Appl. Math. Model., 2021, 95, 89-105. doi: 10.1016/j.apm.2021.02.006 [11] J. R. Graef, L. Kong, A. Ledoan and M. Wang, Stability analysis of a fractional online social network model, Math. Comput. Simulat., 2020, 178, 625-645. doi: 10.1016/j.matcom.2020.07.012 [12] G. Huang, Y. Takeuchi, W. Ma and D. Wei, Global stability for delay SIR and SEIR epidemic models with nonlinear incidence rate, Bull. Math. Biol., 2010, 72, 1192-1207. doi: 10.1007/s11538-009-9487-6 [13] H. Kheiri and M. Jafari, Stability analysis of a fractional order model for the HIV/AIDS epidemic in a patchy environment, J. Comput. Appl. Math., 2019, 346, 323-339. doi: 10.1016/j.cam.2018.06.055 [14] Q. Kong, A Short Course in Ordinary Differential Equations, Springer, New York, 2015. [15] A. Lahrouz, R. Hajjami, M. E. Jarroudi and A. Settati, Mittag-Leffler stability and bifurcation of a nonlinear fractional model with replase, J. Comput. Appl. Math., 2021, 386, 113247. doi: 10.1016/j.cam.2020.113247 [16] Y. Li, Y. Chen and I. Podlubny, Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability, Comput. Math. Appl., 2010, 59, 1810-1823. doi: 10.1016/j.camwa.2009.08.019 [17] Z. Lu, Y. Yu, Y. Chen, G. Ren, C. Xu, S. Wang and Z. Yin, A fractional-order SEIHDR model for COVID-19 with inter-city networked coupling effects, Nonlinear Dyn., 2020, 101, 1717-1730. doi: 10.1007/s11071-020-05848-4 [18] M. Martcheva and C. Castillo-Chavez, Diseases with chronic stage in a population with varying size, Math. Biosci., 2003, 182, 1-25. doi: 10.1016/S0025-5564(02)00184-0 [19] C. C. McCluskey and Y. Yang, Global stability of a diffusive virus dynamics model with general incidence function and time delay, Nonlinear Anal. RWA., 2015, 25, 64-78. doi: 10.1016/j.nonrwa.2015.03.002 [20] I. Podlubny, Fractional Differential Equations, Academic Press, New York, 1999. [21] B. Reade, R. G. Bowers, M. Begon and R. Gaskell, A model of disease and vaccination for infections with acute and chronic phases, J. Theor. Biol., 1998, 190, 55-367. [22] T. Sardar, S. Rana and J. Chattopadhyay, A mathematical model of dengue transmission with memory, Commun. Nonlinear Sci. Numer. Simulat., 2015, 22, 511-525. doi: 10.1016/j.cnsns.2014.08.009 [23] J. L. Schiff, The Laplace Transform: Theory and Applications, Springer, New York, 1999. [24] R. Shi, T. Lu and C. Wang, Dynamic analysis of a fractional-order model for HIV with drug-resistance and CTL immune response, Math. Comput. Simulat., 2021, 188, 509-536. doi: 10.1016/j.matcom.2021.04.022 [25] B. Sounvoravong and S. Guo, Dynamics of a diffusive SIR epidemic model with time delay, J. Nonlinear Model. Anal., 2019, 1, 319-334. [26] R. Su and W. Yang, Global stability of a diffusive HCV infections epidemic model with nonlinear incidence, J. Appl. Math. Comput., 2021. https://doi.org/10.1007/s12190-021-01637-3. doi: 10.1007/s12190-021-01637-3 [27] Y. Wang, Z. Zhao and M. Wang, The transmissibility of hepatitis C virus: a modelling study in Xiamen City, China, Epidemiol. Infect., 2020, 148, e291. doi: 10.1017/S0950268820002885 [28] World Health Organization, Hepatitis C, 2021. https://www.who.int/news-room/fact-sheets/detail/hepatitis-c. [29] Y. Yang and L. Xu, Stability of a fractional order SEIR model with general incidence, Appl. Math. Lett., 2020, 105, 106303. doi: 10.1016/j.aml.2020.106303 [30] Y. Yang, J. Zhou and C. H. Hsu, Threshold dynamics of a diffusive SIRI model with nonlinear incidence rate, J. Math. Anal. Appl., 2019, 478, 874-896. [31] Y. Yang, L. Zou, J. Zhou and C. H. Hsu, Dynamics of a waterborne pathogen model with spatial heterogeneity and general incidence rate, Nonlinear Anal. RWA., 2020, 53, 103065. doi: 10.1016/j.nonrwa.2019.103065 [32] J. Yuan and Z. Yang, Global dynamics of an SEI model with acute and chronic stages, J. Comput. Appl. Math., 2008, 213, 465-476. doi: 10.1016/j.cam.2007.01.042 [33] R. Zhang and Y. Liu, A new Barbalat's lemma and Lyapunov stability theorem for fractional order systems, 29th Chinese control and decision conference (CCDC), IEEE, 2017, 3676-3681. [34] S. Zhang and Y. Zhou, Dynamics and application of an epidemiological model for hepatitis C, Math. Comput. Modell., 2012, 56, 36-42. doi: 10.1016/j.mcm.2011.11.081 [35] Y. Zhou, J. Wang and L. Zhang, Basic Theory of Fractional Differential Equations (Second Edition), World Scientific, Singapore, 2016. -
-
-
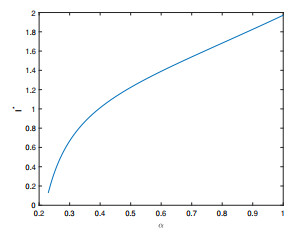
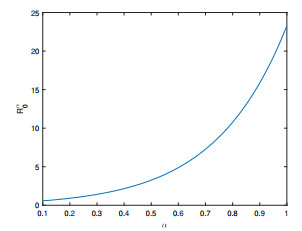
Figure 1. Plot of
$ \mathcal{R}_{0}^{\alpha}$ in terms of α. - Figure 2. Plot of I* in terms of α.
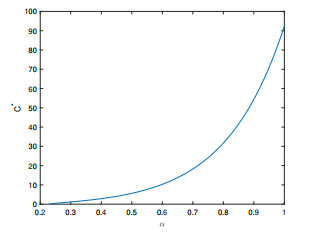
- Figure 3. Plot of C* in terms of α.
-
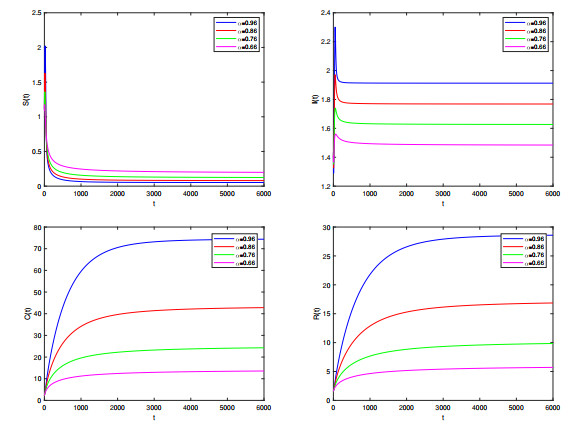
Figure 4. Dynamics of system (5.1) for different values
$ \alpha $ when$ \mathcal{R}_{0}^{\alpha}>1 $ . -
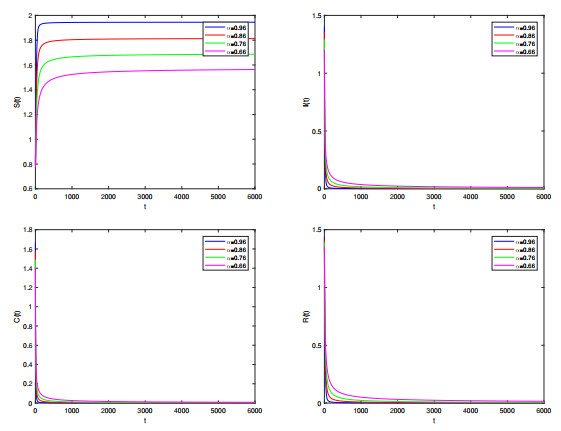
Figure 5. Dynamics of system (5.1) for different values
$ \alpha $ when$ \mathcal{R}_{0}^{\alpha}<1 $ .




 DownLoad:
DownLoad: