| Citation: | Tim Hopkins, Emrah Kılıç. ANALYTICALLY EXPLICIT INVERSE OF A KIND OF PERIODIC TRIDIAGONAL MATRIX USING A BACKWARD CONTINUED FRACTION APPROACH[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2299-2313. doi: 10.11948/20210441 |
ANALYTICALLY EXPLICIT INVERSE OF A KIND OF PERIODIC TRIDIAGONAL MATRIX USING A BACKWARD CONTINUED FRACTION APPROACH
-
Abstract
We present a fast algorithm for generating the inverse and the determinant of an extended, periodic, tridiagonal matrix. We use backward continued fractions to generate the elements of the inverse in closed form. By trading memory use against the cost of repeating the computation of certain quantities we are able to produce an effective procedure for a symbolic algebra implementation. We compare the performance of our Maple implementation with that of the standard Maple library procedures for matrix inversion and computation of the determinant on a set of illustrative example matrices.
-

-
References
[1] J. Ao and J. Sun, Matrix representations of Sturm-Liouville problems with coupled eigenparameter-dependent boundary conditions, Applied Mathematics and Computation, 2014, 244, 142–148. [2] A. Ayzenberg, Space of isospectral periodic tridiagonal matrices, Algebr. Geom. Topol., 2020, 20, 2957–2994. doi: 10.2140/agt.2020.20.2957 [3] M. G. Beker, G. Cella, R. DeSalvo, et al., Improving the sensitivity of future GW observatories in the 1–10 Hz band: Newtonian and seismic noise, General Relativity and Gravitation, 2011, 43(2), 623–656. doi: 10.1007/s10714-010-1011-7 [4] A. Bunse-Gerstner, R. Byers and V. Mehrmann, A chart of numerical methods for structured eigenvalue problems, SIAM J. Matrix Anal. Appl., 1992, 13(2), 419–453. doi: 10.1137/0613028 [5] R. A. Bustos-Marún, E. A. Coronado and H. M. Pastawski, Buffering plasmons in nanoparticle wave guides at the virtual-localized transition, Phys. Rev. B, 2010, 82(3), 035434. [6] B. K. Choudhury, Diffusion of heat in multidimensional composite spherical body, IMA J. Appl. Math., 2013, 78(3), 474–493. [7] C. M. da Fonseca, On the eigenvalues of some tridiagonal matrices, J. Comput. Appl. Math., 2007, 200(1), 283–286. doi: 10.1016/j.cam.2005.08.047 [8] C. M. da Fonseca and V. Kowalenko, Eigenpairs of a family of tridiagonal matrices: three decades later, Acta Mathematica Hungarica, 2019, 160, 376–389. [9] M. Dow, Explicit inverses of Toeplitz and associated matrices, ANZIAM Journal, 2008, 44, E185–E215. doi: 10.21914/anziamj.v44i0.493 [10] M. E. A. El-Mikkawy and F. Atlan, A new recursive algorithm for inverting general k-tridiagonal matrices, Appl. Math. Lett., 2015, 44, 34–39. [11] M. A. El-Shehawey, G. A. El-Shreef and A. S. Al-Henawy, Analytical inversion of general periodic tridiagonal matrices, J. Math. Anal. Appl., 2008, 345, 123–134. doi: 10.1016/j.jmaa.2008.04.002 [12] K. Filipiak, A. Markiewicz and A. Sawikowski, Determinants of multidiagonal matrices, Electron. J. Linear Al., 2012, 25, 102–188. [13] C. F. Fischer and R. A. Usmani, Properties of some tridiagonal matrices and their application to boundary value problems, SIAM J. Numer. Anal., 1969, 6(1), 127–142. [14] Y. Fu, X. Jiang, Z. Jiang and S. Jhang, Inverses and eigenpairs of tridiagonal Toeplitz matrix with opposite-bordered rows, J. Appl. Anal. Comput., 2020, 10(4), 1599–1613. [15] T. Hopkins and E. Kılıç, An analytical approach: Explicit inverses of periodic tridiagonal matrices, Journal of Computational and Applied Mathematics, 2018, 335, 207–226. [16] W. B. Jones and W. J. Thron, Continued fraction, analytic theory and applications, Addison Wesley, Reading, MA, 1980. [17] E. Kılıç, Explicit formula for the inverse of a tridiagonal matrix by backward continued fractions, Appl. Math. Comput., 2008, 197(1), 345–357. [18] D. H. Lehmer, D. M. Smiley, M. F. Smiley and J. Williamson, Solution to problem E710, The American Mathematical Monthly, 1946, 53(9), 534–535. [19] Maplesoft, a division of Waterloo Maple Inc., Maple 2019, Waterloo, Ontario, Canada. [20] R. M. M. Mattheij and M. D. Smooke, Estimates for the inverse of tridiagonal matrices arising in boundary-value problems, Linear Algebra Appl., 1986, 73, 33–57. [21] G. Meurant, A review on the inverse of symmetric tridiagonal and block tridiagonal matrices, SIAM J. Matrix Anal. Appl., 1992, 13(3), 707–728. [22] L. G. Molinari, Determinants of block tridiagonal matrices, Linear Algebra Appl., 2008, 429, 2221–2226. [23] Wolfram Research, Inc., Mathematica, Version 12.0. Champaign, IL, 2019. -
-
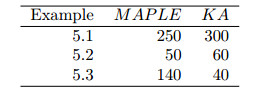
- Figure 1. Comparison of execution times for MAPLE and KA on the test problems
- Figure 2. Comparison of the maximum order of the test examples that can be inverted in less than 10 seconds.





 DownLoad:
DownLoad: