| Citation: |
Ashish, Jinde Cao. DYNAMICAL INTERPRETATIONS OF A GENERALIZED CUBIC SYSTEM[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2314-2329. doi: 10.11948/20210455
|
DYNAMICAL INTERPRETATIONS OF A GENERALIZED CUBIC SYSTEM
-
Abstract
Chaotic map is a typical route in mathematics to describe the dynamical interpretations in various applications of science and engineering. However, the dynamics in the traditional logistic chaotic map $ r\vartheta(1-\vartheta) $ depends on the single control parameter $ r $. In this article, a generalized cubic chaotic map with three changeable parameters $ a $, $ b $ and $ r $ is introduced and its dynamical properties are studied. The added new control parameter increases the flexibility in the system due to which it can fit in various applications. A few cases are discussed showing the effectiveness of the changeable parameters in various properties such as stationary and periodic states, stability in stationary states, Lyapunov exponent property, bifurcation interpretation, and the minimum entropy control. Further, the developments are illustrated mathematically as well as experimentally followed by period-doubling bifurcation and Lyapunov exponent diagrams. Moreover, it is noticed that as compared to traditional chaotic systems, a bifurcation self-similarity is seen along the x-axis in all the cases of the cubic map. Moreover, a brief summary on Shannon minimum entropy is also given to control the unstable stationary and periodic states in chaotic regime.
-
Keywords:
- Bifurcation plot /
- cubic map /
- Lyapunov exponent /
- entropy
-
-
References
[1] K. T. Alligood, T. D. Sauer and J. A. Yorke, Chaos : An Introduction to Dynamical Systems, Springer Verlag, New York Inc., 1996. [2] O. Alpar, Analysis of a new simple one dimensional chaotic map, Nonlinear Dyn., 2014, 78, 771–778. doi: 10.1007/s11071-014-1475-1 [3] M. Andrecut, Logistic map as a random number generator, Int. J. Mod. Phys. B., 1998, 12(921), 101–102. [4] D. Aniszewska, New discrete chaotic multiplicative maps based on the logistic map, Int. J. Bifurc. Chaos, 2018, 28(9), 7. [5] Ashish, J. Cao and R. Chugh, Chaotic behavior of logistic map in superior orbit and an improved chaos-based traffic control model, Nonlinear Dyn., 2018, 94(2), 959–975. doi: 10.1007/s11071-018-4403-y [6] Ashish and J. Cao, A novel fixed point feedback approach studying the dynamcial behaviour of standard logistic map, Int. J. Bifurc. Chaos, 2019, 29(1), 16. [7] Ashish, J. Cao and R. Chugh, Controlling chaos using superior feedback technique with applications in discrete traffic models, Int. J. Fuzzy Syst., 2019, 21(5), 1467–1479. doi: 10.1007/s40815-019-00636-8 [8] Ashish, J. Cao and R. Chugh, Discrete chaotification in modulated logistic system, Int. J. Bifurc. Chaos, 2021, 31(5), 14. [9] Ashish, J. Cao, F. Alsaadi and A. K. Malik, Discrete Superior Hyperbolicity in Chaotic Maps, Chaos: Theory and Applications, 2021, 3(1), 34–42. doi: 10.51537/chaos.936679 [10] Ashish, M. Rani and R. Chugh, Julia sets and Mandelbrot sets in Noor orbit, Appl. Math. Comput., 2014, 228, 615–631. [11] D. Baleanu, G. Wu, Y. Bai and F. Chen, Stability analysis of Caputo–like discrete fractional systems, Commun. Nonlinear Sci. Numer. Simulat., 2017, 48, 520–530. doi: 10.1016/j.cnsns.2017.01.002 [12] M. S. Baptista, Cryptography with chaos, Phy. Lett. A, 1998, 240, 50–54. doi: 10.1016/S0375-9601(98)00086-3 [13] J. Cao, Ashish and F. Alsaadi, Chaotic evolution of difference equations in Mann orbit, J. Appl. Anal. Comput., 2021, 11(6), 3063–3082. [14] R. Chugh, M. Rani and Ashish, Logistic map in Noor orbit, Chaos and Complexity Letters, 2012, 6(3), 167–175. [15] A. R. Chowdhary and M. Debnath, Periodicity and Chaos in Modulated Logistic map, Int. J. Theor. Phy., 1990, 29(7), 779–788. doi: 10.1007/BF00673913 [16] R. L. Devaney, A First Course in Chaotic Dynamical Systems: Theory and Experiment, Addison-Wesley, 1992. [17] J. E. Disbro and M. Frame, Traffic flow theory and chaotic behavior, Transp. Res. Rec., 1990, 1225, 109–115. [18] L. P. L. de Oliveira and M. Sobottka, Cryptography with chaotic mixing, Chaos Solitons Fractals, 2008, 3(35), 466–471. [19] M. J. Feigenbaum, Quantitative universality for a class of nonlinear transformations, J. Stat. Phys., 1978, 19(1), 25–52. doi: 10.1007/BF01020332 [20] A. Garfinkel, M. L. Spano, W. L. Ditto and J. N. Weiss, Controlling cardiac chaos, Science, 1992, 257, 1230–1235. doi: 10.1126/science.1519060 [21] D. Grether, A. Neumann and K. Nagel, Simulation of urban traffic control: A queue model approach, Procedia Comput. Sci., 2012, 10, 808–814. [22] S. C. Lo and H. J. Cho, Chaos and control of discrete dynamic traffic model, J. Franklin Inst., 2005, 342, 839–851. [23] K. Malek, and F. Gobal, Application of chaotic logistic map for the interpretation of anion-insertion in poly-ortho-aminophenol films, Synth. Met., 2000, 11, 167–171. [24] R. May, Simple mathematical models with very complicated dynamics, Nature, 1976, 261, 459–475. [25] H. Poincare, Les Methods Nouvells de la Mecanique Leleste, Gauthier Villars, Paris, 1899. [26] H. Sadeghian, K. Merat, H. Salarieh and A. Alasty, On the fuzzy minimum entropy control to stabilize the unstable fixed points of chaotic maps, Appl. Math. Model., 2011, 3(35), 1016–1023. [27] H. Salarieh and A. Alasty, Stabilizing unstable fixed points of chaotic maps via minimum entropy control, Chaos Solitons Fractals, 2008, 37, 763–769. [28] N. Singh and A. Sinha, Chaos-based secure communication system using logistic map, Opt. Lasers Eng., 2010, 48, 398–404. [29] Y. Wang, S. Liu and H. Li, On fractional difference logistic maps: Dynamic analysis and synchronous control, Nonlinear Dyn., 2020, 102, 579–588. [30] J. N. Weiss, A. Garfinkel, M. L. Spano and W. L. Ditto, Chaos and chaos control in biology, J. Clin. Invest., 1994, 93, 1355–1360. [31] G. Wu and D. Baleanu, Discrete fractional logistic map and its chaos, Nonlinear Dyn., 2014, 75, 283–286. [32] G. Wu and D. Baleanu, Discrete chaos in fractional delayed logistic map, Nonlinear Dyn., 2015, 80, 1697–1703. -
-
Figures(5)
Export File
Citation
Ashish, Jinde Cao. DYNAMICAL INTERPRETATIONS OF A GENERALIZED CUBIC SYSTEM[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2314-2329. doi: 10.11948/20210455
Format
Content
DownLoad:
-
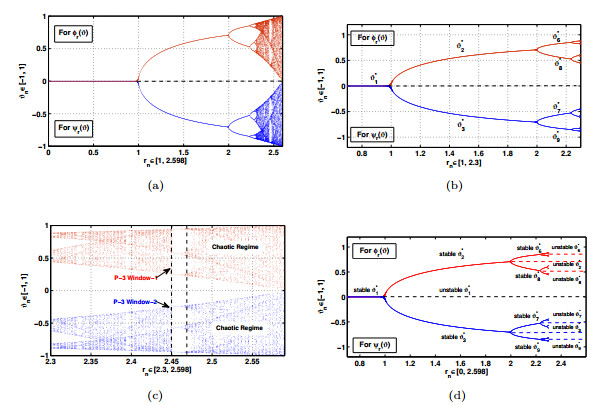
Figure 1. (a) Bifurcation plot for the cubic map
$ r \vartheta(1- \vartheta^2) $ when$ \vartheta \in [-1, 1] $ , (b) Magnified period-doubling regime for the cubic map$ r \vartheta(1- \vartheta^2) $ when$ \vartheta \in [-1, 1] $ , (c) Magnified chaotic regime for the cubic map$ r \vartheta(1- \vartheta^2) $ when$ \vartheta \in [-1, 1] $ , (d) Stabilization in fixed and periodic states for the cubic map$ r \vartheta(1- \vartheta^2) $ -
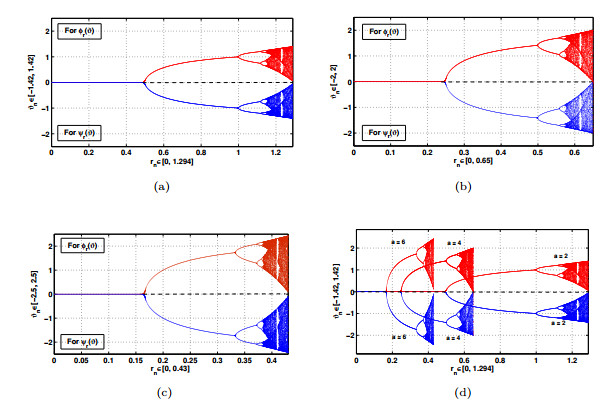
Figure 2. (a) Bifurcation plot for the cubic map
$ r \vartheta(2- \vartheta^2) $ when$ \vartheta \in [-1.42, 1.42] $ , (b) Bifurcation plot for the cubic map$ r \vartheta(4- \vartheta^2) $ when$ \vartheta \in [-2, 2] $ , (c) Bifurcation plot for the cubic map$ r \vartheta(6- \vartheta^2) $ when$ \vartheta \in [-2.5, 2.5] $ , (d) Comparative bifurcation plot for the map$ r \vartheta_n(a-\vartheta_n^2) $ when$ a = 2, 4 $ and$ 6 $ -
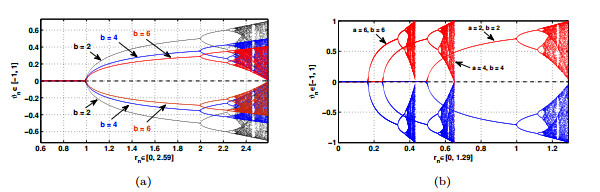
Figure 3. (a) Bifurcation plots for the map
$ r \vartheta_n(1-b\vartheta_n^2) $ when$ b = 2, 4 $ and$ 6 $ , (b) Bifurcation plots for the map$ r \vartheta_n(a-b\vartheta_n^2) $ when$ a, b = 2, 4 $ and$ 6 $ -
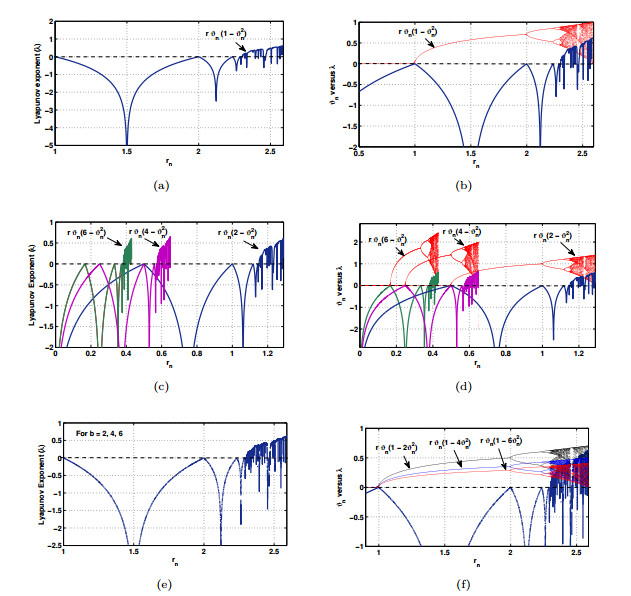
Figure 4. (a) Lyapunov exponent plot for the map
$ r \vartheta_n(1-\vartheta_n^2) $ when$ 0\leq r\leq 2.59 $ , (b) LE versus bifurcation plot for the map$ r \vartheta_n(1-\vartheta_n^2) $ when$ 0\leq r\leq 2.59 $ , (c) Lyapunov exponent plot for the map$ r \vartheta_n(a-\vartheta_n^2) $ when$ a=2, 4 $ and$ 6 $ , (d) LE versus bifurcation plot for the map$ r \vartheta_n(a-\vartheta_n^2) $ when$ a=2, 4 $ and$ 6 $ , (e) Lyapunov exponent plot for the map$ r \vartheta_n(1-b \vartheta_n^2) $ when$ b=2, 4 $ and$ 6 $ , (f) LE versus bifurcation plot for the map$ r \vartheta_n(1-b \vartheta_n^2) $ when$ a=2, 4 $ and$ 6 $ -
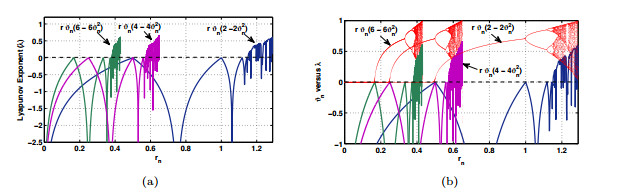
Figure 5. (a) Lyapunov exponent plot for the map
$ r \vartheta_n(a-b \vartheta_n^2) $ when$ a, b=2, 4 $ and$ 6 $ , (b) LE versus bifurcation plot for the map$ r \vartheta_n(a-b \vartheta_n^2) $ when$ a, b =2, 4 $ and$ 6 $