| Citation: |
Ruhai Zhou. EXISTENCE AND COMPUTATION OF INVARIANT ALGEBRAIC CURVES FOR PLANAR QUADRATIC DIFFERENTIAL SYSTEMS[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2330-2348. doi: 10.11948/20210473
|
EXISTENCE AND COMPUTATION OF INVARIANT ALGEBRAIC CURVES FOR PLANAR QUADRATIC DIFFERENTIAL SYSTEMS
-
Abstract
Some necessary conditions are given for the existence of invariant algebraic curves for planar quadratic differential systems in a special canonical form. An efficient algorithm is then designed for computations of invariant algebraic curves. From the algorithm, a quadratic differential system is found with two Hopf bifurcations as the parameter varies, each leading to an invariant algebraic limit cycle of degree 5. A family of degree 6 invariant algebraic limit cycles is also produced. To further demonstrate the capability of the algorithm, we provide a quadratic system with a family of degree 7 invariant algebraic curves enclosing one or two centers, and a system possessing a degree 16 irreducible invariant algebraic curve with a singular point of multiplicity 8 on the curve.
-
-
References
[1] W. Adams and P. Loustaunau, An Introduction to Grobner Bases, Graduate Studies in Mathematics, 3, American Mathematical Society, Providence, RI, 1994. [2] M. Alberich-Carraminana, A. Ferragut and J. Llibre, Quadratic planar differential systems with algebraic limit cycles via quadratic plane Cremona maps, Adv. in Math., 2021, 389, 107924. doi: 10.1016/j.aim.2021.107924 [3] J. Chavarriga, H. Giacomini and J. Llibre, Uniqueness of algebraic limit cycles for quadratic systems, J. Math. Anal. Appl., 2001, 261, 85–99. doi: 10.1006/jmaa.2001.7476 [4] J. Chavarriga, J. Llibre and J. Sorolla, Algebraic limit cycles of quadratic systems, J. Differ. Eqs., 2003, 200, 206–244. [5] C. Christopher, Invariant algebraic curves and conditions for a centre, Proc. Roy. Soc. Edinburgh Sect. A, 1994, 124, 1209–1229. doi: 10.1017/S0308210500030213 [6] C. Christopher and J. Llibre, Integrability via invariant algebraic curves for planar polynomial differential systems, Ann. Diff. Eqs., 2002, 16, 5–19. [7] C. Christopher, J. Llibre, C. Pantazi and X. Zhang, Darboux integrability and invariant algebraic curves for planar polynomial systems, J. Phys. A: Math. Gen., 2002, 25, 2457–2476. [8] C. Christopher, J. Llibre and G. S wirszcz, Invariant algebraic curves of large degree for quadratic systems, J. Math. Anal. Appl., 2005, 303, 450–461. [9] M. Demina and C. Valls, Classification of invariant algebraic curves and nonexistence of algebraic limit cycles in quadratic systems from family (Ⅰ) of the Chinese classification, Int. J. Bifurc. Chaos, 2020, 30(4), 2050056. doi: 10.1142/S021812742050056X [10] F. Dumortier, J. Llibre and J. Artes, Qualitative Theory of Planar Differential Systems, Springer-Verlag, Berlin, 2006. [11] J. Gine, On some open problems in planar differential systems and Hilbert's 16th problem, Chaos, Solitons & Fractals, 2007, 31, 1118–1134. [12] R. Kooji and C. Christopher, Algebraic Invariant curves and the instegrability of polynomial systems, Appl. Math. Lett., 1993, 6, 51–53. [13] G. Leonov, A Criterion for the Existence of Four Limit Cycles in Quadratic Systems, J. Appl. Math. Mech., 2010, 74, 135–143. [14] G. Leonov and O. Kuznetsova, Lyapunov quantities and limit cycles of two-dimensional dynamical systems: analytical methods and symbolic computation, Regul. Chaotic Dyn., 2010, 15, 354–377. [15] J. Llibre, Open problems on the algebraic limit cycles of planar polynomial vector fields, Bull. Acad. Sci., 2008, 56, 19–26. [16] J. Llibre, Integrability and Limit Cycles via First Integrals, Symmetry, 2021, 13, 1736. [17] J. Llibre and G. S wirszcz, Classification of quadratic systems admitting the existence of an algebraic limit cycle, Bull. Sci. Math., 2007, 131, 405–421. [18] J. Llibre and C. Valls, Algebraic limit cycles for quadratic polynomial differential systems, Discr. Contin. Dyn. Ser. B, 2018, 23, 2475–2485. [19] J. Llibre, R. Oliveira and Y. Zhao, On the birth and death of algebraic limit cycles in quadratic differential systems, Euro. Int. Appl. Math., 2021, 32, 317–336. [20] G. Swirszcz, An algorithm for finding invariant algebraic curves of a given degree for polynomial planar vector fields, Int. J. Bifurc. Chaos, 2005, 15, 1033–1044. [21] Wolfram Research, Inc., Mathematica, Version 12.1, Champaign, IL, 2020. [22] Y. Ye, Theory of Limit Cycles, Translations of Mathematical Monographs, 66, American Mathematical Society, Providence, RI, 1986. -
-
Figures(6)
Export File
Citation
Ruhai Zhou. EXISTENCE AND COMPUTATION OF INVARIANT ALGEBRAIC CURVES FOR PLANAR QUADRATIC DIFFERENTIAL SYSTEMS[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2330-2348. doi: 10.11948/20210473
Format
Content
DownLoad:
-
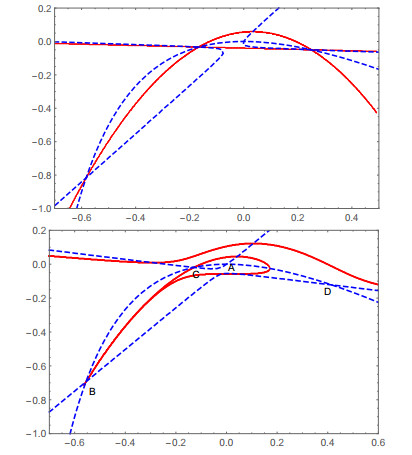
Figure 1. Top: Invariant algebraic limit cycle of degree 5 for the quadratic system (4.1) at
$ s=-\frac{20}{9} $ . Bottom: Another invariant algebraic limit cycle at$ s=\frac{17}{12} $ . The dashed blue curves in this and other figures below are$ \dot x=0 $ and$ \dot y=0 $ , respectively. Their intersections are equilibrium points of the dynamical system. Solid red curves are components of the invariant algebraic curve of the quadratic system. -
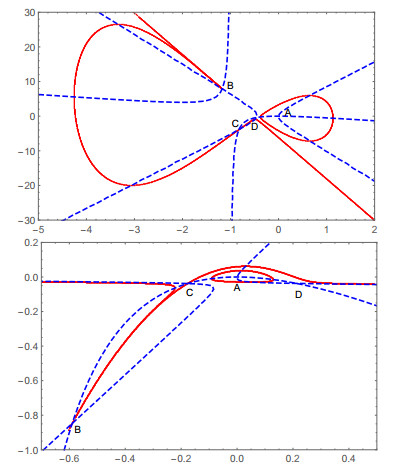
Figure 2. Top: The degree 5 invariant algebraic curve at
$ s=\frac{7}{5} $ for the quadratic system (4.1). There is a heteroclinic loop enclosing the equilibrium point at the origin. For$ s>\frac{7}{5} $ , algebraic limit cycle emerges. Bottom: The degree 5 invariant algebraic curve of (4.1) at$ s=\frac43<\frac{7}{5} $ . It contains a heteroclinic loop connecting two equilibrium points$ B $ and$ C $ . -
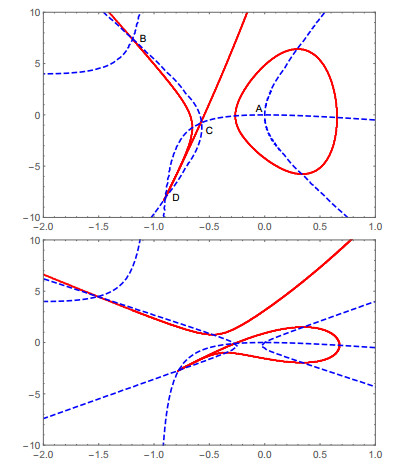
Figure 3. Top: The invariant algebraic curve for the quadratic system (5.1) when
$ s=18 $ . One of the branches is an algebraic limit cycle of degree 6 enclosing the focus at the origin. Bottom: The invariant algebraic curve at$ s=7 $ . One of the branches is a heteroclinic loop enclosing the focus at the origin with a cusp. -
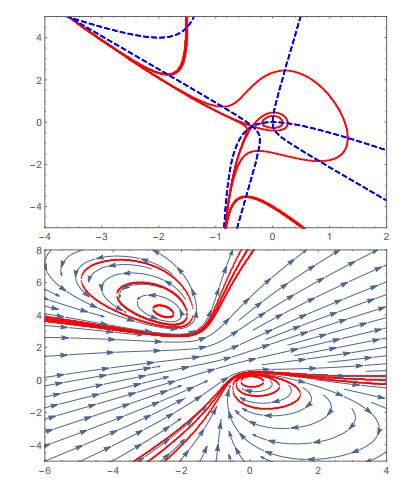
Figure 4. Top: Three invariant algebraic curves of the planar quadratic system (6.1) at
$ b_2=-3 $ . One contains a homoclinic orbit enclosing the center at the origin. Bottom: Six invariant algebraic curves of the planar quadratic system (6.1) at$ b_2=1 $ . Each contains a periodic orbit enclosing one of the two centers and a branch homeomorphic to a straight line. Flow field of the dynamical system is shown in the figure with arrowed lines. -
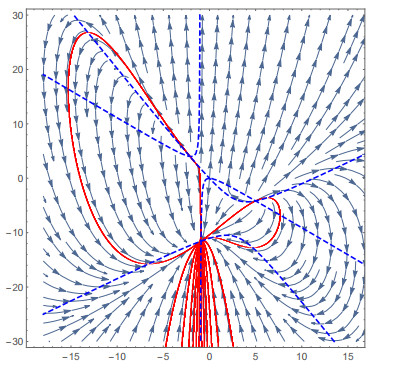
Figure 5. The algebraic curve (solid red) and the vector field (black arrows) of the differential system (7.2). Blue dashed lines are determined by
$ \dot x=0 $ and$ \dot y=0 $ . - Figure 6. Coefficients in the algebraic curve (A.1).