| Citation: | An Ma, Jing Hu, Qimin Zhang. DYNAMIC ANALYSIS AND OPTIMAL CONTROL OF A TOXICANT-POPULATION MODEL WITH REACTION-DIFFUSION[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 579-605. doi: 10.11948/20210438 |
DYNAMIC ANALYSIS AND OPTIMAL CONTROL OF A TOXICANT-POPULATION MODEL WITH REACTION-DIFFUSION
-
Abstract
In this paper, we study the threshold dynamics and optimal control of a toxicant-population model with reaction-diffusion to understand how toxicant affect populations. In order to obtain the extinction and persistent conditions of the toxicant, the basic reproduction number of the model is considered, when $ R_0<1 $, the toxicant-free equilibrium is globally attractive, when $ R_0>1 $, the solution to the system is uniformly persistent. We also introduce the optimal control strategy, with the method of dynamic programming, the Hamilton-Jacobi-Bellman (HJB) equation is constructed and the optimal control is obtained. Finally, we conduct numerical simulations to verify the theoretical analysis.
-

-
References
[1] L. Duan, Q. Lu, Z. Yang and L. Chen, Effects of diffusion on a stage-structured population in a polluted environment, Appl. Math. Comput., 2004, 154(2), 347–359. [2] J. K. Hale, Asymptotic Behavior of Dissipative Systems, American Mathematical Soc., 2010. [3] T. G. Hallam, C. E. Clark and J. S. Jordan, Effects of toxicants on populations: A qualitative approach Ⅱ. First order kinetics, J. Math. Biol., 1983, 18(1), 25–37. doi: 10.1007/BF00275908 [4] T. G. Hallam, C. E. Clark and R. R. Lassiter, Effects of toxicants on populations: A qualitative approach Ⅰ. Equilibrium environmental exposure, Ecol. Model., 1983, 18(3–4), 291–304. doi: 10.1016/0304-3800(83)90019-4 [5] T. G. Hallam and J. L. D. Luna, Effects of toxicants on populations: A qualitative approach Ⅲ. Environmental and food chain pathways, J. Theor. Biol., 1984, 109(3), 411–429. doi: 10.1016/S0022-5193(84)80090-9 [6] J. He and K. Wang, The survival analysis for a single-species population model in a polluted environment, Appl. Math. Model, 2007, 31, 2227–2238. doi: 10.1016/j.apm.2006.08.017 [7] Higham and J. Desmond, An algorithmic introduction to numerical simulations of stochastic differential equations, SIAM Rev., 2001, 43, 525–546. doi: 10.1137/S0036144500378302 [8] Y. Jin and F. Wang, Dynamics of a benthic-drift model for two competitive species, J. Math. Anal. Appl., 2018, 462, 840–860. doi: 10.1016/j.jmaa.2017.12.050 [9] T. Kang, Y. Du, M. Ye and Q. Zhang, Approximation of invariant measure for a stochastic population model with Markov chain and diffusion in a polluted environment, Math. Biosci. Eng., 2020, 17(6), 6702–6719. doi: 10.3934/mbe.2020349 [10] T. Kang, Q. Zhang and H Wang, Optimal control of an avian influenza model with multiple time delays in state and control variables, Discrete. Cont. Dyn. -B, 2017, 22(11). [11] W. Li, M. Ye, Q. Zhang and Y. Li, Numerical approximation of a stochastic age-structured population model in a polluted environment with Markovian switching, Numer. Meth. Part. D. E., 2020. [12] J. Liang, Q. Yan, C. Xiang and S. Tang, A reaction-diffusion population growth equation with multiple pulse perturbations, Commun. Nonlinear. Sci., 2019, 74, 122–137. doi: 10.1016/j.cnsns.2019.02.015 [13] B. Liu, L. Chen and Y. Zhang, The effects of impulsive toxicant input on a population in a polluted environment, J. Biol. Syst., 2003, 11(03), 265–274. doi: 10.1142/S0218339003000907 [14] M. Liu and K. Wang, Survival analysis of stochastic single-species population models in polluted environments, Ecol. Model., 2009, 220(9–10), 1347–1357. doi: 10.1016/j.ecolmodel.2009.03.001 [15] M. Liu and K. Wang, Survival analysis of a stochastic single-species population model with jumps in a polluted environment, Int. J. Biomath., 2016, 9(01), 207–221. [16] Z. Luo and Z. R. He, Optimal control for age-dependent population hybrid system in a polluted environment, Appl. Math. Comput., 2014, 228, 68–76. [17] Z. Ma, G. Cui and W. Wang, Persistence and extinction of a population in a polluted environment, Math. Biosci., 1990, 101(1), 75–97. doi: 10.1016/0025-5564(90)90103-6 [18] P. Magal and X. Q. Zhao, Global attractors and steady states for uniformly persistent dynamical systems, SIAM. J. Math. Anal., 2005, 37, 251–275. doi: 10.1137/S0036141003439173 [19] R. H. Martin and H. L. Smith, Abstract functional differential equations and reaction-diffusion systems, Trans. Amer. Math. Soc., 1990, 321, 1–44. [20] T. Mekkaoui and A. Atangana, Trinition the complex number with two imaginary parts: Fractal, chaos and fractional calculus, Chaos Solitons Fract., 2019, 128, 366–381. doi: 10.1016/j.chaos.2019.08.018 [21] T. Mekkaoui and A. Atangana, Capturing complexities with composite operator and differential operators with non-singular kernel, Chaos Interdiscipl J. Nonlinear Sci., 2019, 29(2). [22] A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations, Springer-Verlag, 1983. [23] G. P. Samanta and A. Maiti, Dynamical model of a single-species system in a polluted environment, J. Appl. Math. Comput., 2004, 16(1–2), 231–242. [24] A. J. Shaw, Ecological Genetics of Plant Populations in Polluted Environment, Springer, New York, 1991. [25] H. L. Smith, Monotone dynamical systems: An introduction to the theory of competitive and cooperative systems, Amer. Math. Soc., 1995, 41. [26] H. L. Smith and X. Q. Zhao, Robust persistence for semidynamical systems, Nonlinear Anal-Theor., 2001, 47(9), 6169–6179. doi: 10.1016/S0362-546X(01)00678-2 [27] H. R. Thieme, Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity, SIAM J. Appl. Math., 2009, 70, 188–211. doi: 10.1137/080732870 [28] J. Wang and X. Wu, Dynamics and profiles of a diffusive cholera model with bacterial hyperinfectivity and distinct dispersal rates, J. Dyn. Differ. Equ., 2021, (2), 1–37. [29] W. Wang and X. Q. Zhao, Basic reproduction numbers for reaction-diffusion epidemic models, SIAM J. Appl. Dyn. Syst., 2012, 11(4), 1652–1673. doi: 10.1137/120872942 [30] X. Wang and X. Q. Zhao, Target reproduction numbers for reaction-diffusion population models, J. Math. Biol., 2020, 81(2), 625–647. doi: 10.1007/s00285-020-01523-9 [31] Y. Wang, J. Shi and J. Wang, Persistence and extinction of population in reaction-diffusion-advection model with strong Allee effect growth, J. Math. Biol., 2019. [32] Y. Wu and X. Zou, Dynamics and profiles of a diffusive host-pathogen system with distinct dispersal rates, J. Differ. Equ., 2018, 264, 4989–5024. doi: 10.1016/j.jde.2017.12.027 [33] J. Yong and X. Zhou, Stochastic Controls: Hamiltonian Systems and HJB Equations, Springer, 1999. [34] X. Yu, S. Yuan and T. Zhang, Survival and ergodicity of a stochastic phytoplankton-zooplankton model with toxin producing phytoplankton in an impulsive polluted environment, Appl. Math. Comput., 2019, 347, 249–264. [35] X. Q. Zhao, Dynamical Systems in Population Biology, Springer, 2003. [36] Y. Zhao, S. Yuan and Q. Zhang, Numerical solution of a fuzzy stochastic single-species age-structure model in a polluted environment, Appl. Math. Comput., 2015, 260, 385–396. -
-
-
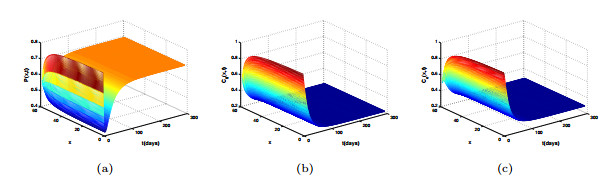
Figure 1.
The evolution of
$ P $ $ C_0 $ $ C_e $ $ \mathcal{R}_0=0.17<1 $ -
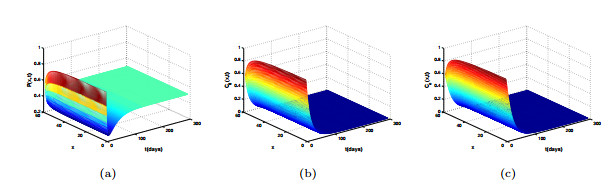
Figure 2.
The evolution of
$ P $ $ C_0 $ $ C_e $ $ \mathcal{R}_0=1.8>1 $ -
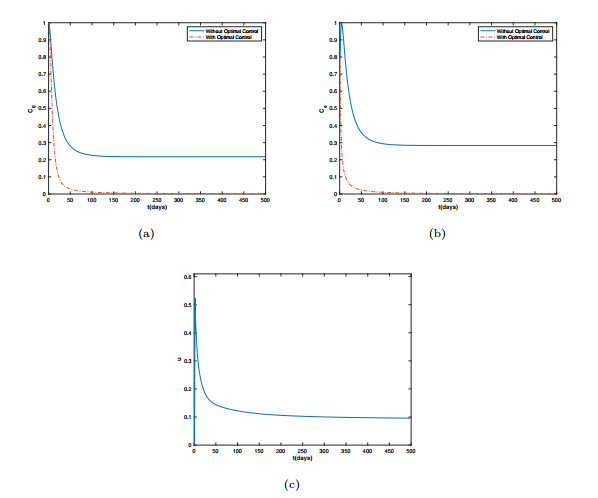
Figure 3.
The paths of the optimal state variables
$ C_0 $ $ C_e $ $ u $




 DownLoad:
DownLoad: