| Citation: | Emadidin Gahalla Mohmed Elmahdi, Jianfei Huang. EFFICIENT NUMERICAL SOLUTION OF TWO-DIMENSIONAL TIME-SPACE FRACTIONAL NONLINEAR DIFFUSION-WAVE EQUATIONS WITH INITIAL SINGULARITY[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 831-849. doi: 10.11948/20210444 |
EFFICIENT NUMERICAL SOLUTION OF TWO-DIMENSIONAL TIME-SPACE FRACTIONAL NONLINEAR DIFFUSION-WAVE EQUATIONS WITH INITIAL SINGULARITY
-
Abstract
In this paper, we present an efficient linearized alternating direction implicit (ADI) scheme for two-dimensional time-space fractional nonlinear diffusion-wave equations with initial singularity. First, the original problem is equivalently transformed into its partial integro-differential form. Then, for the time discretization, the Crank-Nicolson technique combined with the midpoint formula and the second order convolution quadrature formula are used. Meanwhile, the classical central difference formula and fractional central difference formula are adopted to approximate the second order derivative and the Riesz derivative in space, respectively. The unconditional stability and convergence of the proposed scheme are proved by the energy method. Numerical experiments support the theoretical results.
-

-
References
[1] A. H. Bhrawya, E. H. Doha, D. Baleanu and S. S. Ezz-Eldien, A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations, J. Comput. Phys., 2015, 293, 142-156. doi: 10.1016/j.jcp.2014.03.039 [2] H. Chen, S. Lü and W. Chen, A unified numerical scheme for the multi-term time fractional diffusion and diffusion-wave equations with variable coefficients, J. Comput. Appl. Math., 2018, 330, 380-397. doi: 10.1016/j.cam.2017.09.011 [3] A. Chen and C. Li, Numerical solution of fractional diffusion-wave equation, Numer. Func. Anal. Opt., 2016, 37(1), 19-39. doi: 10.1080/01630563.2015.1078815 [4] C. Celik and M. Duman, Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative, J. Comput. Phys., 2012, 231, 1743–1750. doi: 10.1016/j.jcp.2011.11.008 [5] H. Chen, D. Xu and J. Zhou, A second-order accurate numerical method with graded meshes for an evolution equation with a weakly singular kernel, J. Comput. Appl. Math., 2019, 356, 152-163. doi: 10.1016/j.cam.2019.01.031 [6] A. Ebadian, H. R. Fazli and A. A. Khajehnasiri, Solution of nonlinear fractional diffusion-wave equation by traingular functions, SeMA. J., 2015, 72, 37-46. doi: 10.1007/s40324-015-0045-x [7] E. G. M. Elmahdi and J. Huang, Two linearized finite difference schemes for time fractional nonlinear diffusion-wave equations with fourth order derivative, AIMS Mathematics, 2021, 6(6), 6356-6376. doi: 10.3934/math.2021373 [8] W. Fan, X. Jiang, F. Liu and V. Anh, The unstructured mesh finite element method for the two-dimensional multi-term time-space fractional diffusion-wave equation on an irregular convex domain, J. Sci. Comput., 2018, 77, 27-52. doi: 10.1007/s10915-018-0694-x [9] X. Gu, T. Huang, C. Ji and B. Carpentieri, A.A. Alikhanov, Fast iterative method with a second-order implicit difference scheme for time-space fractional convection-diffusion equation, J. Sci. Comput., 2017, 72, 957-985. [10] J. Huang, Y. Tang, L. Vázquez and J. Yang, Two finite difference schemes for time fractional diffusion-wave equation, Numer. Algor., 2013, 64, 707-720. doi: 10.1007/s11075-012-9689-0 [11] J. Huang, S. Arshad, Y. Jiao and Y. Tang, Convolution quadrature methods for time-space fractional nonlinear diffusion-wave equations, East Asian J. Appl. Math., 2019, 9, 538-557. doi: 10.4208/eajam.230718.131018 [12] J. Huang, D. Yang and L. O. Jay, Efficient methods for nonlinear time fractional diffusion-wave equations and their fast implementations, Numer. Algorithms, 2020, 85(2), 375-397. doi: 10.1007/s11075-019-00817-4 [13] J. Huang, J. Zhang, S. Arshad, Y. Jiao and Y. Tang, A superlinear convergence scheme for the multi-term and distribution-order fractional wave equation with initial singularity, Numer. Methods Partial Differential Eq., 2021, 37(4), 2833-2848. doi: 10.1002/num.22773 [14] J. Huang, J. Zhang, S. Arshad and Y. Tang, A numerical method for two-dimensional multi-term time-space fractional nonlinear diffusion-wave equations, Appl. Numer. Math., 2021, 159, 159-173. doi: 10.1016/j.apnum.2020.09.003 [15] C. Ji and Z. Sun, An unconditionally stable and high-order convergent difference scheme for Stokes' first problem for a heated generalized second grade fluid with fractional derivative, Numer. Math. Theor. Meth. Appl., 2017, 10, 597-613. doi: 10.4208/nmtma.2017.m1605 [16] R. J. Le Veque, Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems, SIAM, Philadelphia, 2007. [17] C. Li, Z. Zhao and Y. Chen, Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion, Comput. Math. Appl., 2011, 62, 855-875. doi: 10.1016/j.camwa.2011.02.045 [18] C. Li and F. Zeng, Numerical Methods for Fractional Calculus, Chapman and Hall/CRC, New York, 2015. [19] H. Liao, D. Li and J. Zhang, Sharp error estimate of the nonuniform $L1$ formula for linear reaction-subdiffusion equations, SIAM J. Numer. Anal., 2018, 56, 1112-1133. doi: 10.1137/17M1131829 [20] L. Liu, L. Zheng, F. Liu and X. Zhang, Anomalous convection diffusion and wave coupling transport of cells on comb frame with fractional Cattaneo-Christov flux, Commun. Nonlinear Sci. Numer. Simul., 2016, 38, 45-58. doi: 10.1016/j.cnsns.2016.02.009 [21] Q. Liu, F. Zeng and C. Li, Finite difference method for time-space fractional Schrödinger equation, Int. J. Comput. Math., 2015, 92, 1439-1451. doi: 10.1080/00207160.2014.945440 [22] C. Lubich, Discretized fractional calculus, SIAM J. Math. Anal., 1986, 17, 704-719. doi: 10.1137/0517050 [23] C. Lubich, Convolution quadrature and discretized operational calculus I, Numer. Math., 1988, 52, 129-145. doi: 10.1007/BF01398686 [24] Y. Luchko and F. Mainardi, Some properties of the fundamental solution to the signalling problem for the fractional diffusion-wave equation, Cent. Eur. J. Phys., 2013, 11, 666-675. [25] P. Lyu and S. Vong, A high-order method with a temporal nonuniform mesh for a time-fractional Benjamin-Bona-Mahony equation, J. Sci. Comput., 2019, 80, 1607-1628. doi: 10.1007/s10915-019-00991-6 [26] F. Mainardi, The fundamental solutions for the fractional diffusion-wave equation, Appl. Math. Lett., 1996, 9, 23-28. doi: 10.1016/0893-9659(96)00089-4 [27] R. Metzler and T. F. Nonnenmacher, Space- and time-fractional diffusion and wave equations, fractional Fokker-Planck equations, and physical motivation, Chem. Phys., 2002, 284, 67-90. doi: 10.1016/S0301-0104(02)00537-2 [28] L. Qiao and D. Xu, Compact alternating direction implicit scheme for integro-differential equations of parabolic type, J. Sci. Comput., 2018, 76(1), 565-582. doi: 10.1007/s10915-017-0630-5 [29] M. Stynes, E. ÓRiordan and J. L. Gracia, Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation, SIAM J. Numer. Anal., 2017, 55, 1057-1079. doi: 10.1137/16M1082329 [30] Z. Sun, The Method of Order Reduction and Its Application to the Numerical Solutions of Partial Differential Equations, Science Press, Beijing, 2009. [31] Z. Wang, S. W. Vong and S. Lei, Finite difference schemes for two-dimensional time-space fractional differential equations, Int. J. Comput. Math., 2016, 93(3), 578-595. doi: 10.1080/00207160.2015.1009902 [32] P. Wang and C. Huang, An energy conservative difference scheme for the nonlinear fractional Schröinger equations, J. Comput. Phys., 2015, 293, 238-251. doi: 10.1016/j.jcp.2014.03.037 [33] F. Zeng, Second-order stable finite difference schemes for the time-fractional diffusion-wave equation, J. Sci. Comput., 2015, 65(1), 411-430. doi: 10.1007/s10915-014-9966-2 [34] J. Zhang, T. Aleroev, Y. Fang and J. Huang, Numerical schemes for time-space fractional vibration equations, Adv. Appl. Math. Mech., 2020, 13, 806-826. -
-
-
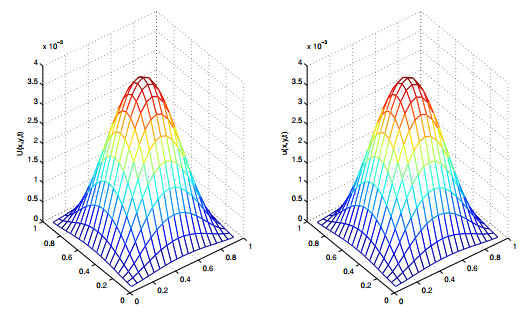
Figure 1. Numrical solution (left column) and exact solution (right column) when
$ \tau =1/16 $ ,$ h=1/20 $ ,$ \sigma=1.4 $ ,$ \alpha=1.6 $ , and$ \beta = 1.5 $ -
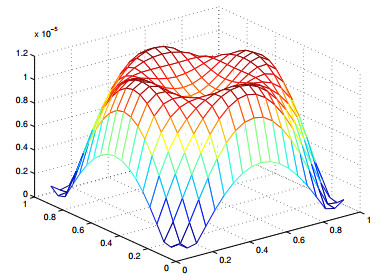
Figure 2. The error surface between numerical solutions and exact solutions for
$ \tau =1/16 $ ,$ h=1/20 $ ,$ \sigma=1.4 $ ,$ \alpha=1.6 $ , and$ \beta = 1.5 $




 DownLoad:
DownLoad: