| Citation: |
Xiangshuo Liu, Lijun Zhang, Mingji Zhang. STUDIES ON PULL-IN INSTABILITY OF AN ELECTROSTATIC MEMS ACTUATOR: DYNAMICAL SYSTEM APPROACH[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 850-861. doi: 10.11948/20210479
|
STUDIES ON PULL-IN INSTABILITY OF AN ELECTROSTATIC MEMS ACTUATOR: DYNAMICAL SYSTEM APPROACH
-
Abstract
The pull-in instability of an electrostatic microstructures is a common undesirable phenomenon which implies the loss of reliability of micro-electromechanical systems. It is important to better understand its mechanism and then to reduce the occurrence of such phenomenon. Our work is devoted to analyzing the pull-in instability of a typical electrostatic micro-electro-mechanical-system actuators with edge effects. The pull-in phenomenon and the dynamic threshold are examined via dynamical system approach and the qualitative theory of differential equations. Nonlinear interplays between the voltage and the initial positions are characterized, from which critical voltage values are identified. Those critical voltages play crucial roles in our analysis. Effects from other system parameters are also examined numerically. It turns out that most of the parameters involved in the MEMS oscillator have corresponding threshold values, beyond which the pull-in instability occurs.
-
-
References
[1] S. Ai and J. A. Pelesko, Dynamics of a canonical electrostatic MEMS/NEMS system, Journal of Dynamics and differential Equations, 2008, 20(3), 609-641. doi: 10.1007/s10884-007-9094-x [2] N. Anjum and J. He, Nonlinear dynamic analysis of vibratory behavior of a graphene nano/microelectromechanical system, Mathematical Methods in the Applied Sciences, 2020, DOI: 10.1002/mma.6699. [3] O. Akar, T. Akin and K. Najafi, A wireless batch sealed absolute capacitive pressure sensor, Sensors & Actuators A Physical, 2001, 95(1), 29-38. [4] D. Elata and H. Bamberger, On the dynamic pull-in of electrostatic actuators with multiple degrees of freedom and multiple voltage sources, Journal of Microelectromechanical Systems, 2006, 15(1), 131-140. doi: 10.1109/JMEMS.2005.864148 [5] M. Gomez, D. E. Moulton and D. Vella, Delayed pull-in transitions in overdamped MEMS devices, Journal of Micromechanics and Microengineering, 2018, 28, 015006. doi: 10.1088/1361-6439/aa9a70 [6] J. He, N. Qie, C. He, et al., Fast identification of the pull-in voltage of a nano/micro-electromechanical system, Journal of Low Frequency Noise, Vibration and Active Control, 2022, 0(0), 1-6. [7] L. Jang, W. Kan, M. Chen, et al., Parameter extraction from BVD electrical model of PZT actuator of micropumps using time-domain measurement technique, Microfluidics and Nanofluidics, 2009, 7, 559-568. doi: 10.1007/s10404-009-0416-7 [8] J. Li, Geometric Properties and Exact Travelling Wave Solutions for the Generalized Burger-Fisher Equation and the Sharma-Tasso-Olver Equation, Journal of Nonlinear Modeling and Analysis, 2019, 1(1), 1-10. [9] C. Liu and Y. Yan, Resonances and chaos of electrostatically actuated arch micro/nanoresonators with time delay velocity feedback, Chaos Solitons & Fractals, 2019, 131, 109512. [10] G. Michael, V. Dominic and M. Derek, Pull-in dynamics of overdamped microbeams, Journal of Micromechanics and Microengineering, 2018, 28, 115002. doi: 10.1088/1361-6439/aad72f [11] C. T. C. Nguyen, L. P. B. Katehi and G. M. Rebeiz, Micromachined devices for wireless communications, Proceedings of the IEEE, 1998, 86, 1756-1768. doi: 10.1109/5.704281 [12] A. H. Nayfeh, M. I. Younis and E. M. Abdel-Rahman, Dynamic pull-in phenomenon in MEMS resonators, Nonlinear Dynamics, 2007, 48(1-2), 153-163. doi: 10.1007/s11071-006-9079-z [13] Y. Nemirovsky and O. Bochobza-Degani, A Methodology and Model for the Pull-In Parameters of Electrostatic Actuators, Journal of Microelectromechanical Systems, 2001, 10(4), 601-614. doi: 10.1109/84.967384 [14] H. C. Nathanson, W. E. Newell, R. A. Wickstrom, et al., The resonant gate transistor, IEEE Transactions on Electron Devices, 1967, 14(3), 117-133. doi: 10.1109/T-ED.1967.15912 [15] G. H. Nielson and G. Barbastathis, Dynamic pull-in of parallel-plate and torsional electrostatic MEMS actuators, Journal of Microelectromechanical Systems, 2006, 15(4), 811-821. doi: 10.1109/JMEMS.2006.879121 [16] H. M. Ouakad, Nonlinear structural behavior of a size-dependent MEMS gyroscope assuming a non-trivial shaped proof mass, Microsystem Technologies, 2019, 26(6), 573-582. [17] H. B. Palmer, The Capacitance of a Parallel-Plate Capacitor by the Schwartz-Christoffel Transformation, American Institute of Electrical Engineers Transactions of Electrical Engineers, 1937, 56(3), 363-366. doi: 10.1109/T-AIEE.1937.5057547 [18] H. Shang, Pull-in instability of a typical electrostatic MEMS resonator and its control by delayed feedback, Nonlinear Dynamics, 2017, 90, 171-183. doi: 10.1007/s11071-017-3653-4 [19] S. Schonhardt, J. G. Korvink, J. Mohr, et al., Optimization of an electromagnetic comb drive actuator, Sensors & Actuators A Physical, 2009, 154(2), 212-217. [20] H. M. Sedighi, M. Changizian and A. Noghrehabadi, Dynamic pull-in instability of geometrically nonlinear actuated micro-beams based on the modified couple stress theory, Latin American Journal of Solids and Structures, 2014, 11(5), 810-825. doi: 10.1590/S1679-78252014000500005 [21] H. A. C. Tilmans, R. Legtenberg, H. Schurer, et al., (Electro-) mechanical characteristics of electrostatically driven vacuum encapsulated polysilicon resonators, IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 1994, 41, 4-6. [22] F. Tajaddodianfar, M. Yazdi and H. N. Pishkenari, Nonlinear dynamics of MEMS/NEMS resonators: analytical solution by the homotopy analysis method, Microsystem Technologies, 2017, 03, 1-14. [23] D. Tian, Q. T. Ain and N. Anjum, Fractal N/MEMS: from pull-in instability to pull-in stability, Fractals, 2020, 29(2), 2150030. [24] M. I. Younis, MEMS linear and nonlinear statics and dynamics, Springer, New York, 2011. [25] L. Zhang, Y. Wang, C. M. Khalique, et al., Peakon and cuspon solutions of a generalized Camassa-Holm-Novikov equation, Journal of Applied Analysis and Computations, 2018, 8(6), 1938-1958. doi: 10.11948/2018.1938 -
-
Figures(5)
Export File
Citation
Xiangshuo Liu, Lijun Zhang, Mingji Zhang. STUDIES ON PULL-IN INSTABILITY OF AN ELECTROSTATIC MEMS ACTUATOR: DYNAMICAL SYSTEM APPROACH[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 850-861. doi: 10.11948/20210479
Format
Content
DownLoad:
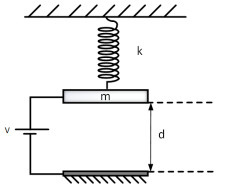
- Figure 1. A single-degree-of-freedom model of a parallel-plate capacitor in a spring-mass system
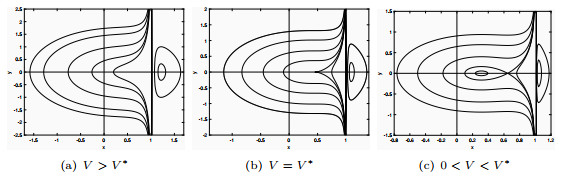
- Figure 2. Phase portraits of system (2.3)
-
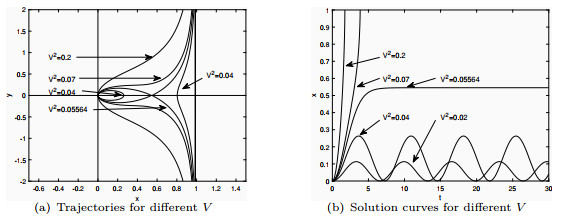
Figure 3. Phase portrait and corresponding solution curves with physical parameters
$ w=1 $ ,$ m=k=\frac{\epsilon}{\pi} $ and$ V=1 $ -
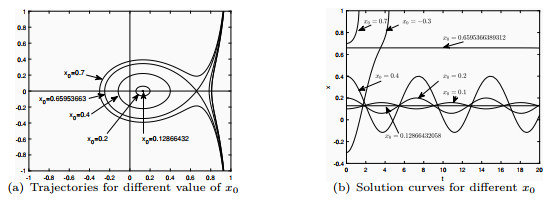
Figure 4. Trajectories and corresponding solution curves with
$ x_0=0 $ and$ w=1 $ and$ m=k=\frac{\epsilon}{\pi} $ . Under the specific setup, one has$ V_c=0.4180909 $ and$ V^*=0.6764614 $ . We also point out that once the value of$ V $ is fixed, the corresponding values for$ x_2, x_c $ and$ x_t $ can be uniquely determined -
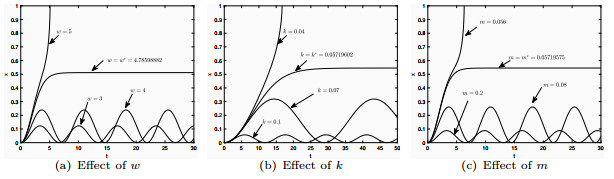
Figure 5. The solution curves of the equation 1.4 with
$ \epsilon=1 $ and$ V=0.1 $ for different setups: (a)$ m=1 $ and$ k=1 $ , (b)$ m=1 $ and$ w=1 $ , (c)$ w=1 $ and$ k=1 $