| Citation: |
Jibin Li, Maoan Han. PLANAR INTEGRABLE NONLINEAR OSCILLATORS HAVING A STABLE LIMIT CYCLE[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 862-867. doi: 10.11948/20210504
|
PLANAR INTEGRABLE NONLINEAR OSCILLATORS HAVING A STABLE LIMIT CYCLE
-
Abstract
In this short paper, by improving some conclusions given by [
2 ], we show that planar integrable nonlinear oscillators can have a stable limit cycle. We also obtain these xact parametric representations of these limit cycles. -
-
References
[1] R. Bellman, Perturbation Techniques in Mathematics, Physics and Engineering, Holt, Rinehart and Winston, New York, 1966. [2] V. K. Chandrasekar, S. N. Pandey, M. Senthilvelan and M. Lakshmanan, A simple and unified approach to identify integrable nonlinear oscillators and systems, J. Math. Phys., 2006, 47, 023508. doi: 10.1063/1.2171520 [3] D. L. Gonzalez and O. Piro, Chaos in a nonlinear driven oscillator with exact solution, Physical Review Letters, 1983, 50(12), 870-872. [4] J. Li, Hilbert's 16th problem and Bifurcations of Planar Polynomial vector Fields, Int. J of Bifurcation and Chaos, 2003, 13(1), 47-106. doi: 10.1142/S0218127403006352 [5] R. Smith, A Simple non-linear Oscillation, J. London Math. Soc., 1961, 36, 33-34. [6] Y. Ye and Others, Theory of Limit Cycles, Trans. Math. Monogr., Amer. Math. Soc., Providence, 1986, 66. -
-
Figures(4)
Export File
Citation
Jibin Li, Maoan Han. PLANAR INTEGRABLE NONLINEAR OSCILLATORS HAVING A STABLE LIMIT CYCLE[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 862-867. doi: 10.11948/20210504
Format
Content
DownLoad:
-
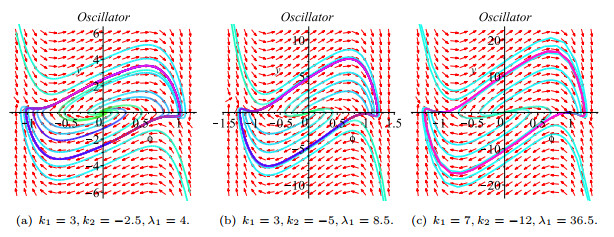
Figure 1. Three phase portraits of system (2) for given parameter group
$ (k_1,k_2,\lambda_1) $ -
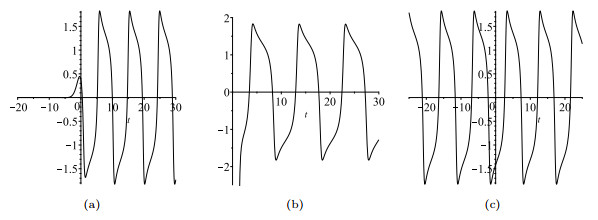
Figure 2. Three graphs of
$ x(t) $ and$ L(t) $ of system (2.2) for given parameter group$ (k_1,k_2,\lambda_1) $ -
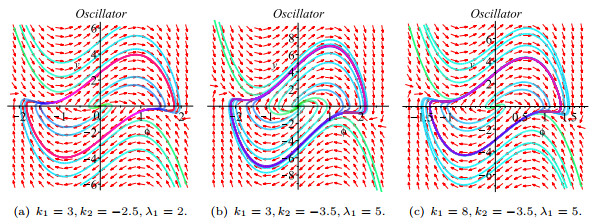
Figure 3. Three phase portraits of system (3.2) for given parameter group
$ (k_1,k_2,\lambda_1) $ -
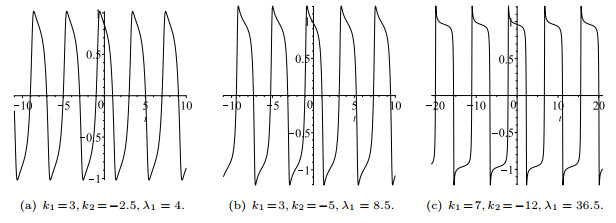
Figure 4. Three graphs of the
$ x- $ component$ L_4(t) $ of the limit cycles for system (12)