| Citation: |
Ningning Ye, Long Zhang, Zhidong Teng. THE DYNAMICAL BEHAVIOR AND PERIODIC SOLUTION IN DELAYED NONAUTONOMOUS CHEMOSTAT MODELS[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 156-183. doi: 10.11948/20210452
|
THE DYNAMICAL BEHAVIOR AND PERIODIC SOLUTION IN DELAYED NONAUTONOMOUS CHEMOSTAT MODELS
-
Abstract
In this paper, the global dynamics and existence of positive periodic solutions in a general delayed nonautonomous chemostat model are investigated. The positivity and ultimate boundedness of solutions are firstly obtained. The sufficient conditions on the uniform persistence and strong persistence of solutions are established. Furthermore, the criterion on the global attractivity of trivial solution is also established. As the applications of main results, the periodic delayed chemostat model is discussed, and the necessary and sufficient criteria on the existence of positive periodic solutions, and uniform persistence and extinction of microorganism species are obtained. Lastly, the numerical examples are presented to illustrate the main conclusions.
-
-
References
[1] P. Amster, G. Robledo and D. Seplveda, Dynamics of a chemostat with periodic nutrient supply and delay in the growth, Nonlinearity, 2020, 33(11), 5839–5860. doi: 10.1088/1361-6544/ab9bab [2] P. Amster, G. Robledo and D. Sepš²lveda, Existence of $\omega$-periodic solutions for a delayed chemostat with periodic inputs, Nonlinear Anal., Real World Appl., 2020, 55, 103134. doi: 10.1016/j.nonrwa.2020.103134 CrossRef $\omega$-periodic solutions for a delayed chemostat with periodic inputs" target="_blank">Google Scholar
[3] E. Beretta and Y. Kuang, Global Stability in a well known delayed chemostat model, Commun. Appl. Anal., 2000, 4(2), 147–155. [4] T. Caraballo, X. Han and P. E. Kloeden, Chemostats with random inputs and wall growth, Math. Methods Appl. Sci., 2015, 38(16), 3538–3550. doi: 10.1002/mma.3437 [5] T. Caraballo, X. Han and P. E. Kloeden, Nonautonomous chemostats with variable delays, SIAM J. Math. Anal., 2015, 47(3), 2178–2199. doi: 10.1137/14099930X [6] G. D'ans, P. Kokotović and D. Gottlieb, A nonlinear regulator problem for a model of biological waste treatment, IEEE Trans. Automat. Control, 1971, 16(4), 341–347. doi: 10.1109/TAC.1971.1099745 [7] S. F. Ellermeyer, S. S. Pilyugin and R. M. Redheffer, Persistence criteria for a chemostat with variable nutrient input, J. Differ. Equ., 2001, 171(1), 132–147. doi: 10.1006/jdeq.2000.4041 [8] R. Fekih-Salem, C. Lobry and T. Sari, A density-dependent model of competition for one resource in the chemostat, Math. Biosci., 2017, 286, 104–122. doi: 10.1016/j.mbs.2017.02.007 [9] X. Feng, J. Tian and X. Ma, Coexistence of an unstirred chemostat model with B-D functional response by fixed point index theory, J. Inequal. Appl., 2016, 2016(1), 294. doi: 10.1186/s13660-016-1241-7 [10] A. G. Fredrickson and G. Stephanopoulos, Microbial competition, Science, 1981, 213(4511), 972–979. doi: 10.1126/science.7268409 [11] H. I. Freedman, J. W. So and P. Waltman, Coexistence in a model of competition in the chemostat incorporating discrete delays, SIAM J. Appl. Math., 1989, 49(3), 859–870. doi: 10.1137/0149050 [12] R. Freter, H. Brickner and S. Temme, An understanding of colonization resistance of the mammalian large intestine requires mathematical analysis, Microecol. Therapy, 1986, 16, 147–155. [13] P. Gajardo, F. Mazenc and H. Ramirez, Competitive exclusion principle in a model of chemostat with delays, Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal., 2009, 16(2), 253–272. [14] M. Gao, D. Jiang, T. Hayat, A. Alsaedi and B. Ahmad, Dynamics of a stochastic chemostat competition model with plasmid-bearing and plasmid-free organisms, J. Appl. Anal. Comput., 2020, 10(4), 1464–1481. [15] J. Harmand, C. Lobry, A. Rapaport and T. Sari, The Chemostat: Mathematical Theory of Microorganism Cultures, ISTE Ltd, London, 2017. [16] S. B. Hsu and P. Waltman, Analysis of a model of two competitors in a chemostat with an external inhibitor, SIAM J. Appl. Math., 1992, 52(2), 528–540. doi: 10.1137/0152029 [17] J. W. M. La Rivière, Microbial Ecology of Liquid Waste Treatment, Springer, Boston, 1977. [18] M. Lin, H. Huo and Y. Li, A competitive model in a chemostat with nutrient recycling and antibiotic treatment, Nonlinear Anal., Real World Appl., 2012, 13(6), 2540–2555. doi: 10.1016/j.nonrwa.2012.02.016 [19] S. Liu, X. Wang, L. Wang and H. Song, Competitive exclusion in delayed chemostat models with differential removal rates, SIAM J. Appl. Math., 2014, 74(3), 634–648. doi: 10.1137/130921386 [20] S. Liu, Bioprocess Engineering: Kinetics, Sustainability, and Reactor Design, Elsevier, Kidlington, 2017. [21] C. Lobry, F. Mazenc and A. Rapaport, Persistence in ecological models of competition for a single resource, C. R. Acad. Sci. Paris, Ser. I, 2005, 340(3), 199–204. doi: 10.1016/j.crma.2004.12.021 [22] N. MacDonald, Time lags in biological models, Springer, New York, 1978. [23] F. Mazenc, S. I. Niculescu and G. Robledo, Stability analysis of mathematical model of competition in a chain of chemostats in series with delay, Appl. Math. Modelling, 2019, 76, 311–329. doi: 10.1016/j.apm.2019.06.006 [24] F. Mazenc, G. Robledo and M. Malisoff, Stability and robustness analysis for a multispecies chemostat model with delays in the growth rates and uncertainties, Discr. Contin. Dyn. Syst. Ser. B, 2018, 23(4), 1851–1872. [25] X. Meng, L. Wang and T. Zhang, Global dynamics analysis of a nonlinear impulsive stochastic chemostat system in a polluted environment, J. Appl. Anal. Comput., 2016, 6(3), 865–875. [26] J. Monod, La technique de culture continue, théorie et applications, Academic Press, New York, 1950. [27] A. Novick and L. Szilard, Experiments with the chemostat on spontaneous mutation of bacteria, Proc. Nat. Acad. Sci., 1950, 36(12), 708–719. doi: 10.1073/pnas.36.12.708 [28] M. Rehim and Z. Teng, Permanence, average persistence and exctinction in nonautonomous single-species growth chemostat models, Adv. Complex Syst., 2006, 9(1), 41–58. [29] M. Rehim and Z. Teng, Mathematical analysis on nonautonomous droop model for phytoplankton growth in a chemostat: boundedness, permanence and extinction, J. Math. Chem., 2009, 46(2), 459–483. doi: 10.1007/s10910-008-9472-6 [30] S. Ruan and X. He, Global stability in chemostat-type competitionmodels with nutrient recycling, SIAM J. Appl. Math., 1998, 58(1), 170–192. doi: 10.1137/S0036139996299248 [31] T. Sari and F. Mazenc, Global dynamics of the chemostat with different rates and variable yields, Math. Biosci. Eng., 2011, 8(3), 827–840. doi: 10.3934/mbe.2011.8.827 [32] S. Sun, C. Guo and X. Liu, Hopf bifurcation of a delayed chemostat model with general monotone response functions, Comp. Appl. Math., 2018, 37(3), 2714–2737. [33] H. L. Smith and P. Waltman, The Theory of the Chemostat, Cambridge University Press, Cambridge, 1995. [34] Z. Teng, Z. Li and H. Jiang, Permanence criteria in non-autonomous predator-prey Kolmogorov systems and its applications, Dyn. Syst., 2004, 19(2), 171–194. [35] Z. Teng and L. Chen, The positive periodic solutions of periodic Kolmogorov type systems with delays (in Chinese), Acta Math. Appl. Sin., 1999, 22(3), 446–456. [36] Z. Teng, L. Nie and X. Fang, The periodic solutions for general periodic impulsive population systems of functional differential equations and its applications, Comp. Math. Appl., 2011, 61(9), 2690–2703. [37] T. F. Thingstad and T. I. Langeland, Dynamics of chemostat culture: the effect of a delay in cell response, J. Theor. Biol., 1974, 48(1), 149–159. [38] P. Waltman, Competition Models in Population Biology, SIAM, Philadelphia, 1983. [39] L. Wang and G. S. K. Wolkowicz, A delayed chemostat model with general nonmonotone response functions and differential removal rates, J. Math. Anal. Appl., 2006, 321(1), 452–468. [40] K. Wang, Z. Teng and X. Zhang, Dynamic behaviors in a droop model for phytoplankton growth in a chemostat with nutrient periodically pulsed input, Discr. Dyn. Nat. Soc., 2012, 2012 (Part 2), 843735. [41] J. Wu, H. Nie and G. S. K. Wolkowicz, The effect of inhibitor on the plasmid-bearing and plasmid-free model in the unstirred chemostat, SIAM J. Math. Anal., 2007, 38(6), 1860–1885. [42] X. Zhang and R. Yuan, Stochastic properties of solution for a chemostat model with a distributed delay and random disturbance, Int. J. Biomath., 2020, 13(7), 2050066. [43] X. Zhao, Dynamical Systems in Population Biology, Springer, London, 2003. -
-
Figures(4)
Export File
Citation
Ningning Ye, Long Zhang, Zhidong Teng. THE DYNAMICAL BEHAVIOR AND PERIODIC SOLUTION IN DELAYED NONAUTONOMOUS CHEMOSTAT MODELS[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 156-183. doi: 10.11948/20210452
Format
Content
DownLoad:
-
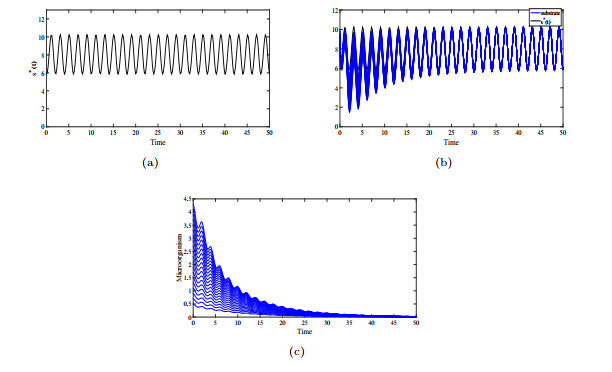
Figure 1.
(a): the numerical simulation of
$ s^*(t) $ $ (s(\eta), x(\eta))=(0.2+0.01i, 3.6+0.01i) $ $ \eta\in[-1.1, 0] $ $ i=1, 2, ... , 20 $ $ t\rightarrow \infty $ -
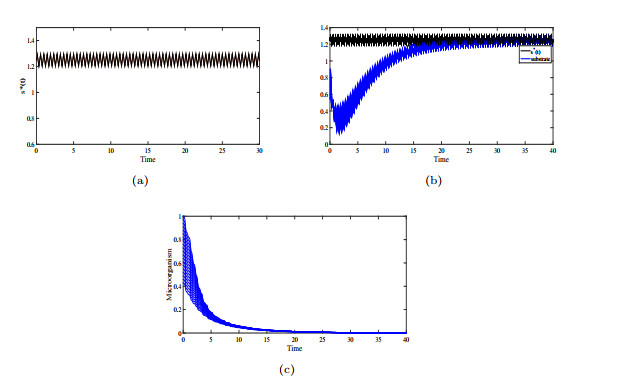
Figure 2.
(a): the numerical simulation of
$ s^*(t) $ $ (s(\eta), x(\eta))=(0.1+0.01i, 0.2+0.01i) $ $ \eta\in[-1, 0] $ $ i=1, 2, ... , 20 $ $ t\rightarrow \infty $ -
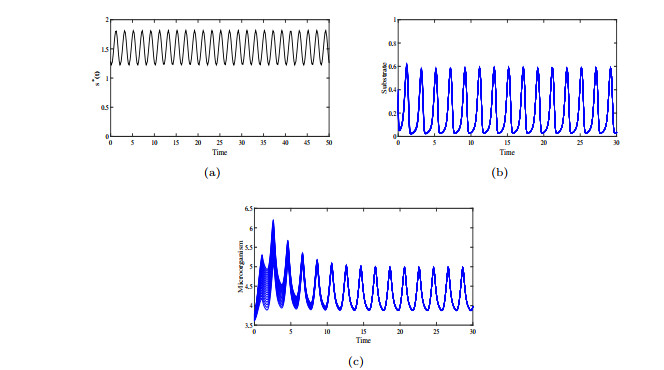
Figure 3.
(a): the numerical simulation of
$ s^*(t) $ $ (s(\eta), x(\eta))=(6.2+0.2i, 0.5+0.2i) $ $ \eta\in[-1.1, 0] $ $ i=1, 2, ... , 20 $ $ (s^*(t), 0) $ $ t\to\infty $ -
Figure 4.
(a): the numerical simulation of
$ s^*(t) $ $ (s(\eta), x(\eta))=(0.5+0.02i, 0.4+0.03i) $ $ \eta\in[-1, 0] $ $ i=1, 2, ... , 20 $ $ (s^*(t), 0) $ $ t\to\infty $