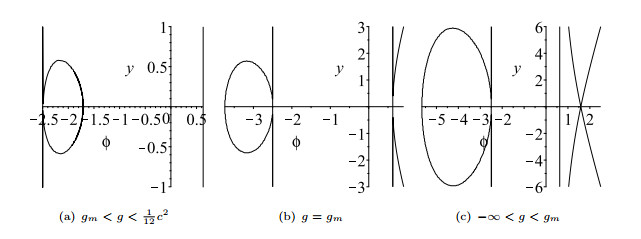| Citation: |
Rong Wu, Jibin Li. MORE EARLY PEAKON MODEL THAN CAMASSA-HOLM EQUATION: BIFURCATIONS AND DYNAMICAL BEHAVIORS OF TRAVELING WAVE SOLUTIONS FOR KUPERSHMIDT'S COUPLED KDV SYSTEM[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1613-1623. doi: 10.11948/20210466
|
MORE EARLY PEAKON MODEL THAN CAMASSA-HOLM EQUATION: BIFURCATIONS AND DYNAMICAL BEHAVIORS OF TRAVELING WAVE SOLUTIONS FOR KUPERSHMIDT'S COUPLED KDV SYSTEM
-
Abstract
This paper considers the traveling wave solutions of Kupershmidt's multicomponent Korteweg-de Vries system derived in 1985. Exploiting the bifurcation theory of planar dynamical systems, we analyze the dynamical behaviors and the bifurcations, and also give all the explicit parametric expressions of solutions when parameters vary. We find that Kupershmidt's model has peakon solutions. This implies that this model is the more early peakon one than Camassa-Holm equation.
-
-
References
[1] A. Arai, Exactly solvable supersymmetric quantum mechanics, J. Math. Anal. Appl., 1991, 158(1), 63-79. doi: 10.1016/0022-247X(91)90267-4 [2] A. Arai, Exact solutions of multi-component nonlinear Schrödinger and Klein-Gordon equations in two-dimensional space-time, J. Phys. A: Math. Gen., 2001, 34(20), 4281-4288. doi: 10.1088/0305-4470/34/20/302 [3] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971. [4] R. Camassa and D. D. Holm, An integrable shallow water equation with peaked solitons, Phys. Rev. Lett., 1993, 71(11), 1661-1664. doi: 10.1103/PhysRevLett.71.1661 [5] R. Camassa, D. D. Holm and J. M. Hyman, A new integrable shallow water equation, Adv. Appl. Mech., 1994, 31, 1-33. doi: 10.1016/S0065-2156(08)70254-0 [6] A. Degasperis, D. D. Holm and A. N. W. Hone, A new integrable equation with peakon solutions, Theoret. and Math. Phys., 2002, 133(2), 1463-1474. doi: 10.1023/A:1021186408422 [7] S. Deng, B. Guo and T. Wang, Some traveling wave solitons of the Green-Naghdi system, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2011, 21(2), 575-585. doi: 10.1142/S0218127411028623 [8] S. Deng, B. Guo and T. Wang, Travelling wave solutions of a generalized Camassa-Holm-Degasperis-Procesi equation, Sci. China Math., 2011, 54(3), 555-572. doi: 10.1007/s11425-010-4122-4 [9] B. Guo and S. Tan, Global smooth solution for a coupled nonlinear wave equations, Math. Methods Appl. Sci., 1991, 14(6), 419-425. doi: 10.1002/mma.1670140606 [10] M. Ito, Symmetries and conservation laws of a coupled nonlinear wave equation, Phys. Lett. A, 1982, 91(7), 335-338. doi: 10.1016/0375-9601(82)90426-1 [11] B. A. Kupershmidt, A coupled Korteweg-de Vries equation with dispersion, J. Phys A, 1985, 18(10), 571-573. doi: 10.1088/0305-4470/18/10/003 [12] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [13] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2007, 17(11), 4049-4065. doi: 10.1142/S0218127407019858 [14] J. Li and Z. Qiao, Peakon, pseudo-peakon, and cuspon solutions for two generalized Cammasa-Holm equations, J. Math. Phys., 2003, 54(12), 1-13, 123501, . [15] J. Li, W. Zhou and G. Chen, Understanding peakons, periodic peakons and compactons via a shallow water wave equation, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2016, 26(12), 1-27, 1650207. [16] L. Zhang and J. Li, Bifurcations of traveling wave solutions in a coupled non-linear wave equation, Chaos, Solitons and Fractals, 2003, 17(5), 941-950. doi: 10.1016/S0960-0779(02)00442-3 -
-
Figures(5)
Export File
Citation
Rong Wu, Jibin Li. MORE EARLY PEAKON MODEL THAN CAMASSA-HOLM EQUATION: BIFURCATIONS AND DYNAMICAL BEHAVIORS OF TRAVELING WAVE SOLUTIONS FOR KUPERSHMIDT'S COUPLED KDV SYSTEM[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1613-1623. doi: 10.11948/20210466
Format
Content
DownLoad:
-
Figure 1. Bifurcations of phase portraits of system (1.7) for a fixed pair
$ (a^2,c) $ . (a) Bifurcation parameter group$ (a^2,c)=(6.25, 5). $ -
Figure 2. The level curve
$ H(\phi,y)=h_s $ for system (1.7) - Figure 3. The wave profiles related to the level curves in Figure 2
-
Figure 4. The level curve
$ H(\phi,y)=h_1 $ for system (1.4) -
Figure 5. The level curve
$ H(\phi,y)=h_2 $ of system (1.7)