| Citation: | Lijun Hong, Bin Wang, Xiaochun Hong. ABELIAN INTEGRALS FOR A KIND OF QUADRATIC REVERSIBLE CENTERS OF GENUS ONE (R7)[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1624-1635. doi: 10.11948/20210487 |
ABELIAN INTEGRALS FOR A KIND OF QUADRATIC REVERSIBLE CENTERS OF GENUS ONE (R7)
-
Abstract
For the quadratic reversible centers of genus one $ (r7) $, its all periodic orbits are quartic curves. Using the method of Picard-Fuchs equation and Riccati equation, we study that the upper bound of the number of zeros for Abelian integrals of system $ (r7) $ under arbitrary polynomial perturbations of degree $ n $, and obtain that the upper bound of the number is $ 45n-72 $ when $ n\geq 2 $, $ 5 $ when $ n=1 $, and $ 0 $ when $ n=0 $, which depends linearly on $ n $.
-

-
References
[1] V. I. Arnold, Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields, Functional Analysis and Its Applications, 1977, 11(2), 85-92. doi: 10.1007/BF01081886 [2] A. Atabaigi, The number of zeros of Abelian integrals for a perturbation of a hyper-elliptic Hamiltonian system with a nilpotent center and a cuspidal loop, Electron. J. Qual. Theo., 2017, 68, 12. [3] A. Braghtha, Darboux systems with a cusp point and pseudo-Abelian integrals, J. Differential Equations, 2020, 268(3), 901-909. doi: 10.1016/j.jde.2019.08.038 [4] C. Christopher and C. Li, Limit cycles of differential equations, Birkhäuser, Basel, 2007. [5] I. E. Colak, J. Llibre and C. Valls, On the bifurcation of limit cycles due to polynomial perturbations of Hamiltonian centers, Mediterr. J. Math., 2017, 14(2), 40(10 pages). [6] Y. Gao, L. Peng and C. Liu, Bifurcation of limit cycles from a class of piecewise smooth systems with two vertical straight lines of singularity, Internat. J. Bifur. Chaos, 2017, 27(10), 1750157(13 pages). [7] S. Gautier, L. Gavrilov and I. D. Iliev, Perturbations of quadratic centers of genus one, Discrete Contin. Dyn. Syst., 2009, 25(2), 511-535. doi: 10.3934/dcds.2009.25.511 [8] M. Han, Bifurcation theory of limit cycles, Science Press, Beijing, 2013. [9] L. Hong, X. Hong and J. Lu, A linear estimation to the number of zeros for Abelian integrals in a kind of quadratic reversible centers of genus one, J. Appl. Anal. Comput., 2020, 10(4), 1534-1544. [10] L. Hong, J. Lu and X. Hong, On the number of zeros of Abelian integrals for a class of quadratic reversible centers of genus one, Journal of Nonlinear Modeling and Analysis, 2020, 2(2), 161-171. [11] X. Hong, J. Lu and Y. Wang, Upper bounds for the associated number of zeros of Abelian integrals for two classes of quadratic reversible centers of genus one, J. Appl. Anal. Comput., 2018, 8(6), 1959-1970. [12] X. Hong, S. Xie and L. Chen, Estimating the number of zeros for Abelian integrals of quadratic reversible centers with orbits formed by higher-order curves, Internat. J. Bifur. Chaos, 2016, 26(2), 1650020(16 pages). [13] X. Hong, S. Xie and R. Ma, On the Abelian integrals of quadratic reversible centers with orbits formed by genus one curves of higher degree, J. Math. Anal. Appl., 2015, 429(2), 924-941. doi: 10.1016/j.jmaa.2015.03.068 [14] E. Horozov and I. D. Iliev, Linear estimate for the number of zeros of Abelian integrals with cubic Hamiltonians, Nonlinearity, 1998, 11(6), 1521-1537. doi: 10.1088/0951-7715/11/6/006 [15] B. Huang and W. Niu, Limit cycles for two classes of planar polynomial differential systems with uniform isochronous centers, J. Appl. Anal. Comput., 2019, 9(3), 943-961. [16] J. Li, Hilbert's 16th problem and bifurcations of planar polynomial vector fields, Internat. J. Bifur. Chaos, 2003, 13(1), 47-106. doi: 10.1142/S0218127403006352 [17] W. Li, Y. Zhao, C. Li and Z. Zhang, Abelian integrals for quadratic centres having almost all their orbits formed by quartics, Nonlinearity, 2002, 15(3), 863-885. doi: 10.1088/0951-7715/15/3/321 [18] C. Liu and D. Xiao, The smallest upper bound on the number of zeros of Abelian integrals, J. Differential Equations, 2020, 269(4), 3816-3852. doi: 10.1016/j.jde.2020.03.016 [19] D. Marín and J. Villadelprat, On the Chebyshev property of certain Abelian integrals near a polycycle, Qual. Theory Dyn. Syst., 2018, 17(1), 261-270. doi: 10.1007/s12346-017-0226-3 [20] P. Moghimi, R. Asheghi and R. Kazemi, An extended complete Chebyshev system of 3 Abelian integrals related to a non-algebraic Hamiltonian system, Comput. Methods Differ. Equ., 2018, 6(4), 438-447. [21] D. Novikov and S. Malev, Linear estimate for the number of zeros of Abelian integrals, Qual. Theory Dyn. Syst., 2017, 16(3), 689-696. doi: 10.1007/s12346-016-0213-0 [22] S. Rebollo-Perdomo and M. U. Santibáñez, Number of zeros of complete Abelian integrals for a primitive rational polynomial with non-trivial global monodromy, Bull Braz Math. Soc., New Series 51, 2020, 697-717. [23] S. Sui and B. Li, Bifurcation of limit cycles from the global center of a class of integrable non-Hamilton systems, J. Appl. Anal. Comput., 2018, 8(5), 1441-1451. [24] Y. Tian and M. Han, Hopf and homoclinic bifurcations for near-Hamiltonian systems, J. Differential Equations, 2017, 262(4), 3214-3234. doi: 10.1016/j.jde.2016.11.026 [25] J. Yang and L. Zhao, The perturbation of a class of hyper-elliptic Hamilton system with a double eight figure loop, Qual. Theory Dyn. Syst., 2017, 16(2), 317-360. doi: 10.1007/s12346-016-0194-z [26] L. Zhao, M. Qi and C. Liu, The cyclicity of period annuli of a class of quintic Hamiltonian systems, J. Math. Anal. Appl., 2013, 403(2), 391-407. doi: 10.1016/j.jmaa.2013.02.016 [27] Y. Zhao and Y. Chen, The cyclicity of quadratic reversible systems with a center of genus one and non-Morsean point, Applied Mathematics and Computation, 2014, 231, 268-275. doi: 10.1016/j.amc.2014.01.006 [28] Y. Zhao, W. Li, C. Li and Z. Zhang, Linear estimate of the number of zeros of Abelian integrals for quadratic centers having almost all their orbits formed by cubics, Sci. China Ser. A, 2002, 45(8), 964-974. doi: 10.1007/BF02879979 -
-
-
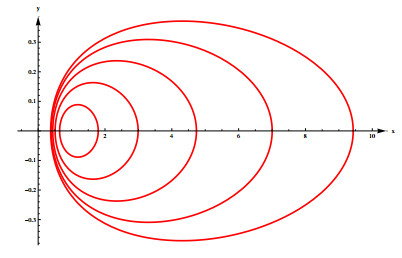
Figure 1. Periodic orbital images of system (
$ r7 $ ).




 DownLoad:
DownLoad: