| Citation: | Amjid Ali, Teruya Minamoto. A NEW NUMERICAL TECHNIQUE FOR INVESTIGATING BOUNDARY VALUE PROBLEMS WITH Ψ-CAPUTO FRACTIONAL OPERATOR[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 275-297. doi: 10.11948/20220062 |
A NEW NUMERICAL TECHNIQUE FOR INVESTIGATING BOUNDARY VALUE PROBLEMS WITH Ψ-CAPUTO FRACTIONAL OPERATOR
-
Abstract
This article introduces a new numerical approach for solving linear and non-linear boundary value problems for Ψ-fractional differential equations (Ψ-FDEs). This approach relies on the Ψ-Haar wavelet operational integration matrices. The Ψ-operational matrices (Ψ-OMs) are used to convert the Ψ-FDE to an algebraic system of equations. The non-linear fractional boundary value problems are first linearized using the quasi-linearization technique, and then the Ψ-Haar wavelet technique is applied to the linearized problem. The solution is updated by the Ψ-Haar wavelet method in each iteration of the quasi-linearization technique. The proposed method is a good and simple mathematical technique for numerically solving non-linear Ψ-FDEs. The operational matrix (OM) method is computationally more efficient. Several linear and non-linear boundary value problems are discussed to demonstrate the applicability, efficiency, and simplicity of the method. Moreover, the error analysis is carried out resulting a rigorous error bound for the proposed method.
-

-
References
[1] R. Almeida, Caputo–hadamard fractional derivatives of variable order, Numerical Functional Analysis and Optimization, 2017, 38(1), 1–19. doi: 10.1080/01630563.2016.1217880 [2] R. Almeida, A caputo fractional derivative of a function with respect to another function, Communications in Nonlinear Science and Numerical Simulation, 2017, 44, 460–481. doi: 10.1016/j.cnsns.2016.09.006 [3] R. Almeida, Fractional differential equations with mixed boundary conditions, Bulletin of the Malaysian Mathematical Sciences Society, 2019, 42(4), 1687–1697. doi: 10.1007/s40840-017-0569-6 [4] R. Almeida, Functional differential equations involving the ψ-caputo fractional derivative, Fractal and Fractional, 2020, 4(2), 29. doi: 10.3390/fractalfract4020029 [5] R. Almeida, M. Jleli and B. Samet, A numerical study of fractional relaxation–oscillation equations involving ψ-caputo fractional derivative, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 2019, 113(3), 1873–1891. [6] R. Almeida, A. B. Malinowska and M. T. T. Monteiro, Fractional differential equations with a caputo derivative with respect to a kernel function and their applications, Mathematical Methods in the Applied Sciences, 2018, 41(1), 336–352. doi: 10.1002/mma.4617 [7] R. Almeida, A. B. Malinowska and T. Odzijewicz, An extension of the fractional gronwall inequality, in Conference on Non-Integer Order Calculus and Its Applications, Springer, 2018, 20–28. [8] R. Almeida, A. B. Malinowska and T. Odzijewicz, On systems of fractional differential equations with the ψ-caputo derivative and their applications, Mathematical Methods in the Applied Sciences, 2021, 44(10), 8026–8041. doi: 10.1002/mma.5678 [9] E. Babolian and A. Shahsavaran, Numerical solution of nonlinear fredholm integral equations of the second kind using haar wavelets, Journal of Computational and Applied Mathematics, 2009, 225(1), 87–95. doi: 10.1016/j.cam.2008.07.003 [10] P. Borisut, P. Kumam, I. Ahmed and W. Jirakitpuwapat, Existence and uniqueness for ψ-hilfer fractional differential equation with nonlocal multi-point condition, Mathematical Methods in the Applied Sciences, 2021, 44(3), 2506–2520. doi: 10.1002/mma.6092 [11] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Progress in Fractional Differentiation & Applications, 2015, 1(2), 73–85. [12] C. Chen and C. Hsiao, Haar wavelet method for solving lumped and distributed-parameter systems, IEE Proceedings-Control Theory and Applications, 1997, 144(1), 87–94. doi: 10.1049/ip-cta:19970702 [13] Y. Chen, M. Yi and C. Yu, Error analysis for numerical solution of fractional differential equation by haar wavelets method, Journal of Computational Science, 2012, 3(5), 367–373. doi: 10.1016/j.jocs.2012.04.008 [14] L. Debnath, Recent applications of fractional calculus to science and engineering, International Journal of Mathematics and Mathematical Sciences, 2003, 2003(54), 3413–3442. doi: 10.1155/S0161171203301486 [15] R. Hilfer, On fractional relaxation, Fractals, 2003, 11(supp01), 251–257. doi: 10.1142/S0218348X03001914 [16] A. Kilbas, Theory and applications of fractional differential equations. [17] Z. Li, Asymptotics and large time behaviors of fractional evolution equations with temporal ψ-caputo derivative, Mathematics and Computers in Simulation, 2022, 196, 210–231. doi: 10.1016/j.matcom.2022.01.023 [18] R. Magin, Fractional calculus in bioengineering begell house publishers, Inc., Connecticut, 2006. [19] F. Norouzi and G. M. N'Guérékata, A study of ψ-hilfer fractional differential system with application in financial crisis, Chaos, Solitons & Fractals: X, 2021, 6, 100056. [20] T. J. Osler, The fractional derivative of a composite function, SIAM Journal on Mathematical Analysis, 1970, 1(2), 288–293. doi: 10.1137/0501026 [21] S. G. Samko, A. A. Kilbas, O. I. Marichev et al., Fractional integrals and derivatives, 1, Gordon and breach science publishers, Yverdon Yverdon-les-Bains, Switzerland, 1993. [22] V. E. Tarasov, Mathematical economics: application of fractional calculus, 2020. -
-
-
Figure 1.
exact and numerical integration of
$ h({t})=\frac{{t}(e^{{t}}+2)}{e+2} $ -
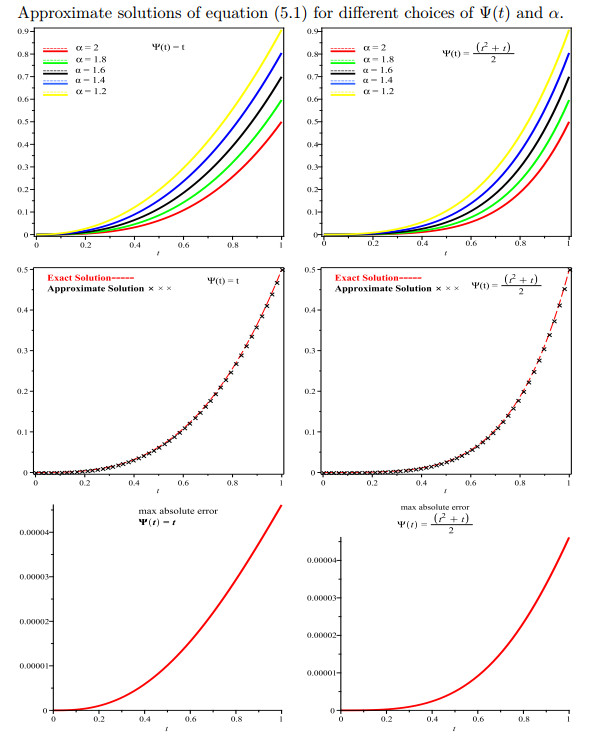
Figure 2.
Exact and Approximate solutions and the corresponding max absolute error of equation (5.1) for
$ \Psi({t})={t} $ $ \Psi({t})=({t}^2+t)/2 $ -
Figure 3.
For equation (5.7). Exact and approximate solutions for
$ {\Psi}({t})={t} $ $ {\Psi}({t})={{t}}^3 $ $ \max $ -
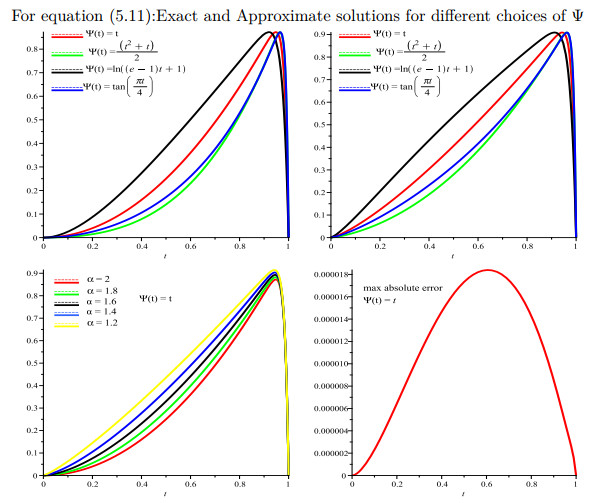
Figure 4.
For equation (5.11): Approximate solutions for different choices of
$ {{\alpha}} $ -
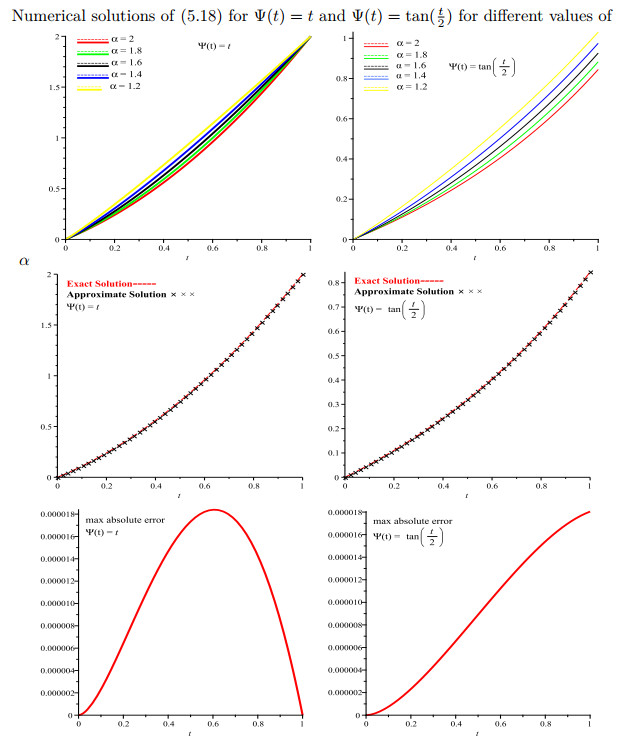
Figure 5.
exact and approximate solutions of (5.18) for
$ {\Psi}({t})={t} $ $ {\Psi}({t})=\tan(\frac{{t}}{2}) $ $ \max $



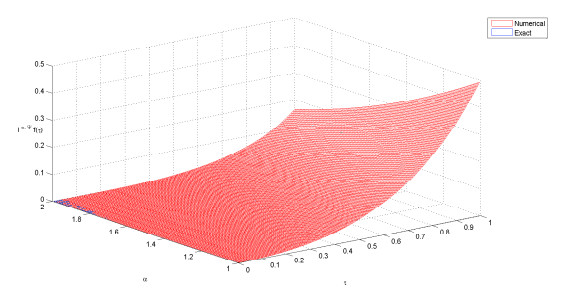

 DownLoad:
DownLoad: