| Citation: | Mingshuo Liu, Huanhe Dong, Yong Fang, Haoyu Dong. MODELLING AND ANALYSIS OF DYNAMIC SYSTEMS ON TIME-SPACE SCALES AND APPLICATION IN BURGERS EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2555-2577. doi: 10.11948/20220067 |
MODELLING AND ANALYSIS OF DYNAMIC SYSTEMS ON TIME-SPACE SCALES AND APPLICATION IN BURGERS EQUATION
-
Abstract
As effective tools that can be used to solve both continuous and discrete dynamic systems, symmetry analysis, conserved quantities and B$ \ddot{a} $cklund transformations of dynamic systems on time-space scales are studied, which unify and generalize the continuous and discrete cases. Applying the method to heat equation and Burgers equation, we get symmetries, group invariant solutions and B$ \ddot{a} $cklund transformations of the system on time-space scales. The results are applied to approximately simulate motion process of traffic flow with given initial condition. The study of nonlinear systems on time-space scales provides a theoretical basis for revealing the internal physical mechanism of the systems. Applications of the method to other dynamic equations on time-space scales deserve to be further studied.
-

-
References
[1] M. R. Ali, W. Ma and R. Sadat, Lie symmetry analysis and wave propagation in variable-coefficient nonlinear physical phenomena, East Asian Journal on Applied Mathematics, 2022, 12(1), 201-212. doi: 10.4208/eajam.100920.060121 [2] P. Amster, C. Rogers and C. C. Tisdell, Existence of solutions to boundary value problems for dynamic systems on a time scale, Journal of Mathematical Analysis and Applications, 2005, 308, 565-577. doi: 10.1016/j.jmaa.2004.11.039 [3] A. Arbi and J. Cao, Pseudo-almost periodic solution on time-space scales for a novel class of competitive neutral-type neural networks with mixed time-varying delays and leakage delays, Neural Processing Letters, 2017, 46, 719-745. doi: 10.1007/s11063-017-9620-8 [4] G. W. Bluman and S. Kumei, Symmetries and differential equations, Springer Science & Business Media, 2013. [5] M. Bohner and A. Peterson, Dynamic equations on time scales: An introduction with applications, Springer Science & Business Media, 2001. [6] M. Bohner and A. Peterson, Advances in dynamic equations on time scales, Birkh$ \ddot{a} $user, Boston, 2003. [7] J. Cheng and J. He, Miura and auto-B$ \ddot{a} $cklund transformations for the discrete KP and mKP hierarchies and their constrained cases, Communications in Nonlinear Science and Numerical Simulation, 2019, 69, 187-197. doi: 10.1016/j.cnsns.2018.09.019 CrossRef $ \ddot{a} $cklund transformations for the discrete KP and mKP hierarchies and their constrained cases" target="_blank">Google Scholar
[8] M. Federson, R. Grau, J. G. Mesquita and E. Toon, Boundedness of solutions of measure differential equations and dynamic equations on time scales, Journal of Differential Equations, 2017, 263(1), 26-56. doi: 10.1016/j.jde.2017.02.008 [9] M. Folly-Gbetoula and D. Nyirenda, Lie symmetry analysis and explicit formulas for solutions of some third-order difference equations, Quaestiones Mathematicae, 2019, 42(7), 907-917. doi: 10.2989/16073606.2018.1499563 [10] R. H. Heredero, D. Levi and P. Winternitz, Symmetries of the discrete Burgers equation, Journal of Physics A: Mathematical and General, 1998, 32(14), 2685-2695. [11] S. Hilger, Ein Maβkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten: Ph. D. thesis, Universität Würzburg, 1988. [12] G. Hovhannisyan, Ablowitz-Ladik hierarchy of integrable equations on a time-space scale, Journal of Mathematical Physics, 2014, 55, 102701. doi: 10.1063/1.4896564 [13] G. Ibolya, and K. Mikula, Numerical solution of the 1D viscous Burgers' and traffic flow equations by the inflow-implicit/outflow-explict finite volume method, Proceedings of ALGORITMY. 2020, 191-200. [14] B. Jackson, Partial dynamic equations on time scales, Journal of Computational and Applied Mathematics, 2006, 186(2), 391-415. doi: 10.1016/j.cam.2005.02.011 [15] C. M. Khalique and O. D. Adeyemo, Soliton solutions, travelling wave solutions and conserved quantities for a three-dimensional soliton equation in plasma physics, Communications in Theoretical Physics, 2021, 73(12), 125003. doi: 10.1088/1572-9494/ac27a1 [16] D. Levi, R. Rebelo and P. Winternitz, Symmetries and integrability of difference equations, Springer, Cham, 2017. [17] T. Meurer and M. Krstic, Finite-time multi-agent deployment: A nonlinear PDE motion planning approach, Automatica, 2011, 47(11), 2534-2542. doi: 10.1016/j.automatica.2011.08.045 [18] T. Nagatani, H. Emmerich and K. Nakanishi, Burgers equation for kinetic clustering in traffic flow, Physica A: Statistical Mechanics and Its Applications, 1998, 255, 158-162. doi: 10.1016/S0378-4371(98)00082-X [19] T. Ozis, E. N. Aksan and A. Ozdes, A finite element approach for solution of Burgers' equation, Applied Mathematics and Computation, 2003, 139, 417-428. doi: 10.1016/S0096-3003(02)00204-7 [20] J. Pu and Y. Chen, Nonlocal symmetries, B$ \ddot{a} $cklund transformation and interaction solutions for the integrable Boussinesq equation, Modern Physics Letters B, 2020, 34(26), 2050288. doi: 10.1142/S0217984920502887 CrossRef $ \ddot{a} $cklund transformation and interaction solutions for the integrable Boussinesq equation" target="_blank">Google Scholar
[21] D. Sun, G. Zhang, W. Liu, M. Zhao, S. Cheng and T. Zhou, Effect of explicit lane changing in traffic lattice hydrodynamic model with interruption, Nonlinear Dynamics, 2016, 86, 269-282. doi: 10.1007/s11071-016-2888-9 [22] H. Sun and W. Li, Existence theory for positive solutions to one-dimensional p-Laplacian boundary value problems on a time scale, Journal of Differential Equations, 2007, 240, 217-248. doi: 10.1016/j.jde.2007.06.004 [23] G. Zhang, L. Ling and Z. Yan, et al., Parity-time-symmetric rational vector rogue waves of the n-component nonlinear Schrödinger equation, Chaos, 2021, 31(6), 063120. doi: 10.1063/5.0048922 [24] J. Zhou and Y. Li, Sobolevs spaces on time scales and its applications to a class of second order Hamiltonian systems on time scales, Nonlinear Analysis-Theory Methods & Applications, 2010, 73(5), 1375-1388. [25] J. Zhou, Z. Shi, H. Zhang and C. Wang, A new lattice model for single-lane traffic flow with the consideration of drivers memory during a period of time, International Journal of Modern Physics C, 2017, 28(6), 1750086. -
-
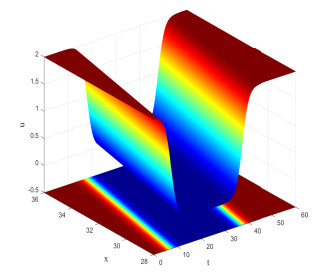
- Figure 1. Space-time evolution of u
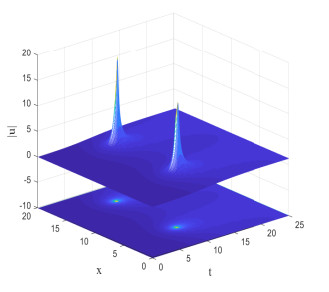
- Figure 2. Space-time evolution of |u|




 DownLoad:
DownLoad: