| Citation: | Xiu Ye, Shangyou Zhang. ORDER TWO SUPERCONVERGENCE OF THE CDG METHOD FOR THE STOKES EQUATIONS ON TRIANGLE/TETRAHEDRON[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2578-2592. doi: 10.11948/20220112 |
ORDER TWO SUPERCONVERGENCE OF THE CDG METHOD FOR THE STOKES EQUATIONS ON TRIANGLE/TETRAHEDRON
-
Abstract
A new conforming discontinuous Galerkin (CDG) finite element method is introduced for solving the Stokes equations. The CDG method gets its name by combining good features of both conforming finite element method and discontinuous finite element method. It has the flexibility of using discontinuous approximation and simplicity in formulation of the conforming finite element method. This new CDG method is not only stabilizer free but also has two order higher convergence rate than the optimal order. This CDG method uses discontinuous $ P_k $ element for velocity and continuous $ P_{k+1} $ element for pressure. Order two superconvergence is derived for velocity in an energy norm and the $ L^2 $ norm. The superconvergent $ P_k $ solution is lifted elementwise to a $ P_{k+2} $ velocity which converges at the optimal order. The numerical experiments confirm the theories.
-

-
References
[1] A. Al-Twaeel, S. Hussian and X. Wang, A stabilizer free weak Galerkin finite element method for parabolic equation, J. Comput. Appl. Math., 2021, 392, 113373. doi: 10.1016/j.cam.2020.113373 [2] A. AL-Taweel, X. Wang, X. Ye and S. Zhang, A stabilizer free weak Galerkin method with supercloseness of order two, Numer. Meth. PDE, 2021, 37, 1012-1029. doi: 10.1002/num.22564 [3] I. Babuška, The finite element method with Lagrangian multiplier, Numer. Math., 1973, 20, 179-192. doi: 10.1007/BF01436561 [4] F. Brezzi, On the existence, uniqueness, and approximation of saddle point problems arising from Lagrangian multipliers, RAIRO, Anal. Numér., 1974, 2, 129-151. [5] G. Chen, M. Feng and X. Xie, A robust WG finite element method for convection–diffusion–reaction equations, J. Comput. Appl. Math., 2017, 315, 107-125. doi: 10.1016/j.cam.2016.10.029 [6] W. Chen, F. Wang and Y. Wang, Weak Galerkin method for the coupled Darcy–Stokes flow, IMA J. Numer. Anal., 2016, 36, 897-921. [7] B. Deka and P. Roy, Weak galerkin finite element methods for parabolic interface problems with nonhomogeneous jump conditions, Numer. Funct. Anal. Optim., 2019, 40, 250-279. [8] V. Girault and P. Raviart, Finite Element Methods for the Navier-Stokes Equations: Theory and Algorithms, Springer-Verlag, Berlin, 1986. [9] Q. Guan, M. Gunzburger and W. Zhao, Weak-Galerkin finite element methods for a second-order elliptic variational inequality, Comput. Methods Appl. Mech. and Engrg., 2018, 337, 677-688 doi: 10.1016/j.cma.2018.04.006 [10] M. D. Gunzburger, Finite Element Methods for Viscous Incompressible Flows, A Guide to Theory, Practice and Algorithms, Academic, San Diego, 1989. [11] Q. Hu, Y. He and K. Wang, Weak galerkin method for the helmholtz equation with DTN boundary condition, Int. J of Numer. Anal. Model., 2020, 17, 643-661. [12] G. Li, Y. Chen and Y. Huang, A new weak Galerkin finite element scheme for general second-order elliptic problems, J. Comput. Appl. Math., 2018, 344, 701-715. [13] R. Lin, X. Ye, S. Zhang and P. Zhu, A weak Galerkin finite element method for singularly perturbed convection-diffusion-reaction problems, SIAM J. Num. Anal., 2018, 56, 1482-1497. doi: 10.1137/17M1152528 [14] J. Liu, S. Tavener, Z. Wang, Lowest-order weak Galerkin finite element method for Darcy flow on convex polygonal meshes, SIAM J. Sci. Comput., 2018, 40, 1229-1252. doi: 10.1137/17M1145677 [15] X. Liu, J. Li and Z. Chen, A weak Galerkin finite element method for the Oseen equations, Adv. Comput. Math., 2016, 42, 1473-1490. [16] L. Mu, X. Ye and S. Zhang, A stabilizer free, pressure robust and superconvergence weak Galerkin finite element method for the Stokes Equations on polytopal mesh, SIAM J. Sci. Comput., 2021, 43, A2614-A2637. [17] W. Qi and L. Song, Weak Galerkin method with implicit $\theta$-schemes for second-order parabolic problems, Appl. Math. and Comp., 2020, 336, 124731. [18] S. Shields, J. Li and E.A. Machorro, Weak Galerkin methods for time-dependent Maxwell's equations, Comput. Math. Appl., 2017, 74, 2106-2124. [19] M. Sun and H. Rui, A coupling of weak Galerkin and mixed finite element methods for poroelasticity, Comput. & Math. with Appl., 2017, 73, 804-823. [20] S. Toprakseven, A weak Galerkin finite element method for time fractional reaction-diffusion-convection problems with variable coefficients, Appl. Numer. Math., 2021, 168, 1-12. [21] S. Xie and P. Zhu, Superconvergence of a WG method for the Stokes equations with continuous pressure, preprint. [22] J. Wang, Q. Zhai, R. Zhang and S. Zhang, A weak Galerkin finite element scheme for the Cahn-Hilliard equation, Math. Comp., 2019, 88, 211-235. [23] C. Wang and J. Wang, Discretization of div–curl systems by weak Galerkin finite element methods on polyhedral partitions, J. Sci. Comput., 2016, 68, 1144-1171. [24] J. Wang and X. Ye, A weak Galerkin finite element method for second-order elliptic problems, J. Comput. Appl. Math., 2013, 241, 103-115. [25] X. Ye and S. Zhang, A stabilizer free weak Galerkin method for the biharmonic equation on polytopal meshes, SIAM J. Numerical Analysis, 2020, 58, 2572-2588, [26] X. Ye and S. Zhang, A conforming discontinuous Galerkin finite element method, Int. J. Numer. Anal. Model., 2020, 17(1), 110-117. [27] X. Ye and S. Zhang, Constructing a CDG element with order two superconvergence for second order problem on rectangular mesh, preprint. [28] H. Zhang, Y. Zou, S. Chai and H. Yue, Weak Galerkin method with $(r, r-1, r-1)$-order finite elements for second order parabolic equations, Appl. Math. and Comp., 2016, 275, 24-40. [29] T. Zhang and T. Lin, A posteriori error estimate for a modified weak Galerkin method solving elliptic problems, Numer. Meth. PDE, 2017, 33, 381-398. [30] A. Zhu, T. Xu and Q. Xu, Weak G alerkin finite element methods for linear parabolic integro-differential equations, Numer. Meth. of PDE, 2016, 32, 1357-1377. [31] S. Zhou, F. Gao, B. Li, and Z. Sun, Weak galerkin finite element method with second-order accuracy in time for parabolic problems, Appl. Math. Lett., 2019, 90, 118-123. -
-
-
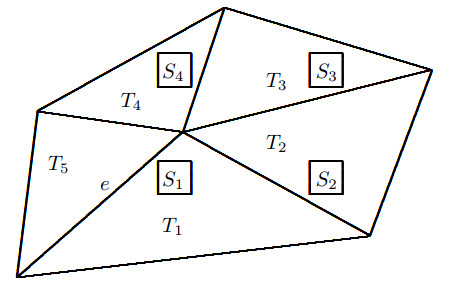
Figure 1. A closed polygon
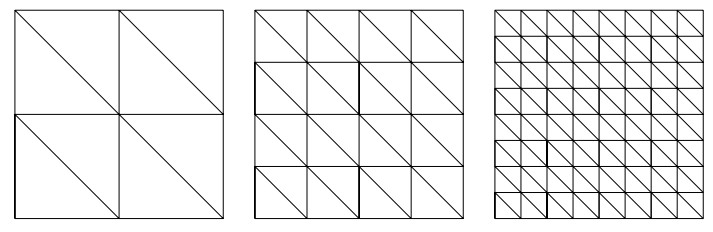
$ U_e=\cup_{i=1}^{5} \overline{T_i} $ contains 4 aligned squares$ \{S_i, i=1, \dots, 4\} $ , for an edge$ e $ , where$ \overline {T_i} $ is the closure of$ T_i $ . - Figure 2. The first three uniform triangular grids for the computation in Tables 1-5.
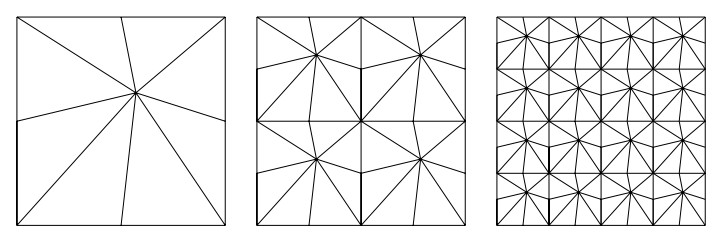
- Figure 3. The first three perturbed triangular grids for the computation in Tables 6-8.




 DownLoad:
DownLoad: